Тема: «События. Комбинация событий. Противоположное событие. Вероятность события. Сложение вероятностей. »
План
1. События. Виды событий.
2. Комбинации событий. Противоположное событие.
3. Вероятность события.
4. Сложение вероятностей.
5. Формирование умений и навыков в решении задач.
Цели и задачи занятия:
Образовательные:
· Изучить основные понятия теории вероятности: событие, виды событий, противоположное событие, вероятность события, независимость событий.
· Рассмотреть некоторые комбинации событий: cумму(объединение) событий, произведение (пересечение) событий.
· Сформулировать теорему о вероятности суммы двух несовместных событий.
· Формировать у обучающихся навыки решения задач по данной теме.
Развивающие:
· Развивать у обучающихся умение учебного труда.
· Развивать умение анализировать, проводить рассуждения.
· Развивать устойчивый интерес к предмету.
Воспитательные:
· Формировать умение аргументировано отстаивать свои взгляды.
· Формировать способность к взаимопомощи, работе в паре, группе, коллективе.
События. Виды событий.
Все, что происходит или не происходит в реальной действительности, называют явлениями или событиями. Если некоторое событие происходит довольно часто, то в его наступлении существует определенная закономерность.
Раздел математики, изучающий закономерности массовых явлений называется теорией вероятностей.
Далее рассмотрим какие же существуют виды событий.
1. Событие, которое в некотором испытании может произойти, а может и не произойти, называют случайным событием.
2. Событие, которое в данном испытании обязательно произойдет, называют достоверным событием.
|
|
3. Событие, которое в данном испытании наступить не может, называют невозможным событием.
Играющий бросает кубик и смотрит, какое число выпало на грани, которая располагается сверху. Какие предположения он может сделать, когда бросает игральный кубик? Например, такие:
событие А – выпадет цифра 1, 2, 3, 4, 5 или 6 – достоверное;
событие В – выпадет цифра 7, 8 или 9 – невозможное;
событие С – выпадет цифра 1– случайное.
4. События несовместны, если появление одного из них исключает появление другого.
Два события, которые в данных условиях могут происходить одновременно, называют совместными, а те, которые не могут происходить одновременно, – несовместимыми.
5. События называются равновозможными, когда в их испытании нет преимуществ.
Комбинации событий. Противоположное событие.
Пусть в определённом испытании могут произойти события А и В. Рассмотрим некоторые комбинации этих событий.
Определение 1. Суммой (объединением) двух событий А и В
называют событие, состоящее в том, что происходит хотя бы одно
из данных событий. Сумму событий А и В обозначают А + В (А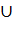 
В).
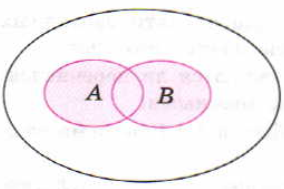
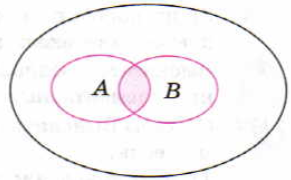На рисунке справа с помощью кругов Эйлера проиллюстрировано понятие суммы событий А и В: большой круг изображает все элементарные события, которые могут произойти в рассматриваемом испытании, левый круг изображает событие А, правый - событие В, а закрашенная область - событие А+В.
Определение 2. Произведением (пересечением) событий А и В
называется событие, состоящее в том, что происходят оба эти
события. Произведение событий А и В обозначают АВ (А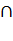 
В).
|
|
Например. Пусть в опыте с бросанием игральной кости события:
А – выпало число очков, кратное 2; В – выпало число очков, кратное 3. Тогда событие А + В означает, что выпало хотя бы одно из чисел 2, 3, 4, 6; событие АВ – выпало число 6.
Задача.1 Пусть из колоды вынимают одну карту. Рассмотрим события: А – это король, В – это карта масти пик.
Тогда: А + В – вынут король или карта масти пик; АВ – из колоды вынут король пик.
Определение 3. События А и В называют равными (равносильными) и пишут А=В, если событие А происходит тогда и только тогда, когда происходит событие В.
Например. В испытании с одним бросанием игрального кубика событие А - выпало число 6, а событие В - выпало наибольшее из возможных чисел, то А=В.
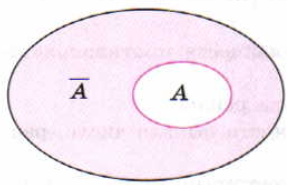
Определение 4. Событие Ā называют противоположным событию А,
если событие Ā происходит тогда и только тогда, когда не происходит
событие А.
Для каждого события А можно рассмотреть противоположное событие Ā, которое наступит тогда и только тогда, когда событие А не наступает. Например: А – выпадение чётного числа очков, Ā – выпадение нечетного числа очков; А – попадание в цель, Ā – промах.
Вероятность события.
Пусть событие А связано с испытанием, имеющим n равновозможных элементарных исходов. И пусть событие A наступает тогда, когда осуществляется один из каких-то m элементарных исходов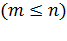 
, и не наступает тогда, когда осуществляется любой из оставшихся (
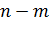) исходов. Тогда говорят, что указанные m исходов, приводящие к наступлению события A, благоприятствуют событию A.
Определение 5. Вероятностью P(A) события A в испытании с равновозможными элементарными исходами называется отношение числа исходов m благоприятствующих событию A, к числу n всех исходов испытания.
|
|
Таким образом, вероятность события A определяется по формуле:
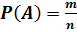. (1)
Здесь n – число всех исходов испытания, m – число исходов, благоприятствующих событию A,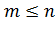 
. Приведённое определение вероятности называют классическим определением вероятности.
Обратите внимание, что в испытании с n равновозможными исходами вероятность наступления каждого элементарного события равна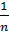 
. Так, например, появление любого из шести чисел 1, 2, 3, 4, 5, 6 после одного бросания игрального кубика имеет вероятность 
.
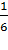Из формулы (1) следует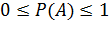 
, а также P(V)=0, P(U)=1,
где V - невозможное событие; U – достоверное событие.
Задача №2: В лотерее из 1000 билетов имеются 200 выигрышных. Вынимают наугад один билет. Чему равна вероятность того, что этот билет выигрышный?
Решение. Общее число различных исходов есть n = 1000. Число исходов, благоприятствующих получению выигрыша, составляет m = 200. Согласно формуле 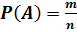, получим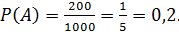 
Ответ: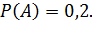 
Задача №3: Из урны, в которой находятся 5 белых и 3 черных шара, вынимают один шар. Найти вероятность того, что шар окажется черным.
Решение. Обозначим событие, состоящее в появлении черного шара, через А. Общее число случаев есть n = 5 + 3. Число случаев m, благоприятствующих появлению события А, равно 3. По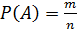 
получим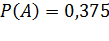 
Ответ: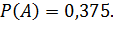 
Задача №4:
Бросают две монеты. Найти вероятность события А - хотя бы на одной монете выпал орёл.
Решение. Обозначим появление орла на выпавшей монете буквой «О», а появление решки - «Р». Тогда равновозможны следующие четыре элементарных исхода испытания (n=4): ОО, РР, ОР и РО. Событию А благоприятствуют следующие 3 пары исходов: ОО, ОР и РО (m=3). Поэтому используя классическое определение вероятности имеем: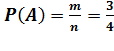 
.
Ответ: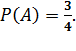 
Сложение вероятностей.
Суммой событий А и В называется событие А + В, состоящее в наступлении либо только события А, либо только события В, либо и события А и события В одновременно.
Теорема о сложении вероятностей. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий, т.е. Р(А+В)=Р(А)+Р(В).
Доказательство.
Следствие: Сумма вероятностей двух противоположных событий равна 1: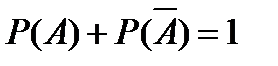 
Доказательство.
