Общие сведения об антенно-фидерных устройствах

Основными характеристиками и параметрами любой антенны являются: радиотехнические, конструктивные, эксплуатационные и экономические.

По своей классификации антенны подразделяются на излучающие провода, использующиеся на частотах до 1ГГц и излучающие поверхности, используемые, в основном, на частотах выше 1ГГц.

В своем большинстве антенны реализуют принцип двойственности, т.е. одну и туже антенну можно использовать как на передачу, так и прием ЭМВ. Однако находят широкое применение и антенны, к которым принцип двойственности не применим (например, антенна бегущей волны, а также активные антенны).

В целях количественной оценки качества функционирования антенн и антенных систем используют радиотехнические показатели, которые разделяются на характеристики и показатели.

Радиотехническими характеристиками называют функциональные зависимости амплитуды, фазы и коэффициента поляризации от направления на точку наблюдения в равноудаленных точках дальней зоны. К ним относятся: 1 – характеристика направленности, 2 – фазовая характеристика, 3 – поляризационная характеристика.

К радиотехническим параметрам антенн относятся: 1 – излучаемая мощность , 2 – сопротивление излучения 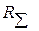, 3 – коэффициент направленного действия (КНД) D, 4 – коэффициент усиления (КУ) G, 5 – коэффициент полезного действия η (КПД), 6 – входное сопротивление, 7 – действующая длина (высота) антенны , 8 – частотный диапазон .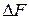

Определение перечисленных характеристик и параметров связано с решением электродинамической задачи. Обычно исходными данными для расчета являются форма и размеры антенны, а также распределение токов (или полей) на ее поверхности. В ходе решения находятся антенные характеристики и параметры. Этот метод называется методом анализа.

Другой метод – метод синтеза. По этому методу по заданным характеристикам и параметрам определяются размеры антенны и распределения в ней токов.

Для определения характеристик и параметров антенны все окружающее ее пространство разбивают на определенные зоны, называемые ближней и дальней.

Ближняя зона – это часть пространства, непосредственно прилегающая к антенне. Расстояние до ее внешней границы можно определить по выражению:

, (7)

где L – линейный размер антенны, λ – длина волны.

В настоящее время теория расчета антенн в ближней зоне не завершена, т.к. в ней не работают основные уравнения теории Максвелла. Особенностями ближней зоны являются: наличие у векторов напряженности электрического E и магнитного Н полей кроме поперечных составляющих еще и продольных составляющих; быстрое уменьшение амплитуды поля с удалением от антенны; комплексность вектора Пойтинга 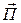; превышение реактивной составляющей мощности поля над активной.

Дальняя зона – это пространство, которое окружает антенну, начиная с внешней границы до бесконечности. Внешнюю границу можно определить из условия:

. (8)

В связи с этим расчет антенных характеристик и параметров осуществляется только в дальней зоне.

На рис.9 представлена система координат, принятая для пояснения этапов расчета антенн. На нем – θ – координата по углу места, φ – координата по азимуту, r – расстояние от антенны до точки наблюдения.

Рисунок 9 – Система координат

На рис.10 представлены некоторые виды антенн, которые нашли широкое применение в различной аппаратуре РЭС.

а – полуволновой вибратор, б – четвертьволновая штыревая антенна, в – рамочная антенна, г – рупорная антенна, д – антенна бегущей волны, е – диэлектрическая антенна, ж – щелевая антенна, з – параболическая антенна, и - печатная (микрополосковая антенна)

Рисунок 10 – Некоторые типы антенн

Характеристика направленности (ХН). ХН – это зависимость амплитуды напряженности поля или плотности потока мощности от направления на точку наблюдения в равноудаленных от антенны точках дальней зоны. Она определяет свойства антенны, заключающиеся в распределении электромагнитной энергии в окружающее пространство. Как

правило, речь идет о напряженности электрического поля Е, имея в виду, что в дальней зоне напряженность магнитного поля находится по простой формуле:

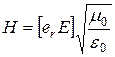, (9)

где e _r - орт сферической системы координат;

ε₀ и μ₀, - магнитная и диэлектрическая проницаемости свободного пространства.

Напряженность поля характеризуется амплитудой, фазой и поляризацией. Можно записать:

(10)

где к=2π/λ, r₀ - расстояние от центра сферической системы координат до точки в дальней зоне (рис.11)

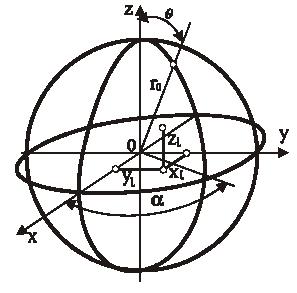
Рисунок 11 – К пояснению свойств диаграммы направленности антенны

Система координат

Назовем соответственно; Ф(θ,α) - амплитудной; ψ(θ,α) - фазовой; е (θ,α) - поляризационной диаграммами направленности. Последняя представляет собой единичный вектор, учитывающий направление вектора Е в дальней зоне.

Используем обозначение:

(11)

Векторную функцию Ф (θ,α) называют комплексной векторной диаграммой направленности. Она объединяет в себе амплитудную, фазовую и поляризационную диаграммы направленности антенны. В большинстве случаев используем обозначение:

(12)

и назовем эту функцию комплексной диаграммой направленности.

Амплитудная диаграмма направленности |Ф(θ,α)| - функция, учитывающая зависимость напряженности поля излученной волны в дальней зоне от углов θ и α.

Нас интересуют антенны, концентрирующие энергию в узком конусе - главном луче антенны. В этом случае |Ф(θ,α)| имеет один главный максимум. Положение этого максимума характеризуется угловыми координатами θ₀ и α₀. Будем считать, что углы θ₀ и α₀ определяют направление максимального излучения антенны. Главный луч антенны характеризуется шириной, которую принято измерять на уровне 0,707 |Ф(θ₀,α₀)|. Ширину луча обозначим через Δθ и α.

Идеальная антенна должна концентрировать всю излученную энергию в главном луче, однако у реальных антенн часть энергии рассеивается за пределами главного луча, образуя боковое излучение, которое характеризуется либо отдельными лепестками, либо общим фоном, занимающим иногда достаточно большие пространственные углы. Боковое излучение будем характеризовать отношением максимальной напряженности поля за пределами главного луча к напряженности поля в направлении максимального излучения; это отношение обозначим через ξ и назовем его уровнем боковых лепестков.

Амплитудная диаграмма направленности определяет распределение потока мощности, излучаемого антенной. Иногда бывает удобно говорить о диаграмме направленности антенны по мощности — Р(θ,α). Очевидно, что

(13)

Т.о., ХН представляет собой поверхность, которую описывает своим концом радиус-вектор r₀ сферической системы координат, величина которого пропорциональна амплитуде напряженности антенного поля в данном направлении. 3-х мерная фигура, получаемая при этом, называется диаграммой направленности (ДН) антенны, или пространственной ХН.

3-х мерное изображение ДН дает полное представление о ХН антенны, однако его представление на плоскости встречает ряд трудностей, поэтому на практике, в основном, используют их сечения в 2-х основных плоскостях – Е и Н. Кроме того, двумерные ДН широко представляются 2-мя способами – в прямоугольной и полярной системе координат. Примеры изображения ДН для рупорной антенны приведены на рис.12.

а	б	в

Рисунок 12 – ДН рупорной антенны: а – 3-х мерное изображение, б – ДН в прямоугольной системе координат, в – ДН в полярных координатах

Фазовая характеристика (ФХ). ФХ антенны называется зависимость фазы излучаемого антенной поля в дальней зоне от направления в пространстве при постоянном расстоянии от фазового центра антенны до точек наблюдения. Функция ψ(θ,α) в выражении (10) и есть ФХ.

Как видно из (10), фаза поля в точках дальней зоны определяется величиной фазового сдвига, складывающегося из двух слагаемых kr ₀ и ψ(θ,α). Первое из них определяет величину фазового сдвига, который получается за счет распространения волны от избранного начала отсчета до рассматриваемой точки. Второе характеризует зависимость фазовых сдвигов уже не от расстояния, а от угловых координат. Смысл зависимости, описываемой функцией ψ(θ,α), таков: если двигаться по поверхности сферы радиусом r₀, описанной вокруг исходного центра (начала отсчета), то зависимость фазовых сдвигов от углов θ и α как раз и будет описываться функцией ψ(θ,α). Эту функцию принято называть фазовой диаграммой направленности антенны.

Для того, чтобы было легче представить себе все особенности, связанные с фазовой диаграммой направленности, полезно ввести в рассмотрение поверхности равных фаз, т. е. поверхности, на которых фаза волны неизменна под всеми углами θ и α. В сферической системе координат поверхности равных фаз описываются следующими функциями, показывающими зависимость от угловых координат длины радиус-вектора каждой точки поверхности:

(14)

причем центр сферической системы здесь тот же, что и центр, от которого отсчитывается r₀.

Если ψ(θ,α) = 0, то это означает, что ρ(θ,α) = r ₀, т. е. поверхность равных фаз - сфера. В этом случае говорят, что антенна имеет фазовый центр и этот центр расположен в центре избранной системы координат. Фазовым центром антенны называется точка, относительно которой фронт волны в дальней зоне имеет вид сферы (за вычетом скачков на λ/2 при переходе через ноль амплитудной диаграммы направленности).

Может оказаться, что поверхности равных фаз суть сферы, но их центры не совпадают с точкой, которая выбрана за начало отсчета. Тогда в формуле (10) ψ(θ,α) не равна нулю, а имеет следующий вид:

(15)

где x_i, y_i, z_i - координаты фазового центра антенны (рис.11).

Как показал А. Р. Вольперт, антенна имеет фазовый центр в том и только в том случае, когда ее фазовая диаграмма направленности имеет вид (15). Иногда фазовую диаграмму направленности вида (15) называют фазовой диаграммой, полученной за счет переноса центра отсчета.

Известно, что в большинстве случаев антенны не имеют фазового центра в том смысле, как он определен выше. Это объясняется тем, что поверхности равных фаз не являются сферами. Однако в большинстве случаев практически важно проанализировать фазовую диаграмму направленности в каком-либо ограниченном секторе, не охватывающем всего пространства. Может оказаться, что в таком ограниченном секторе поверхности равных фаз очень близки к кускам сферических поверхностей. Например, А. Р. Родс назвал фазовым центром антенны центр сферы, которая совпадает с поверхностью равных фаз в пределах главного луча антенны. Вполне обоснованно стремление найти эквивалент фазового центра, когда в строгом смысле он отсутствует, потому что такая точка может рассматриваться как центр, откуда как бы исходит все излучение. Упомянутое определение А. Р. Родса не уточняет, что значит совпадение сферы и поверхности равных фаз. Такое определение не может служить основой для построения математических выражений, позволяющих вычислять координаты интересующей нас точки по известным характеристикам поверхности равных фаз.

Частичным фазовым центром будем называть центр кривизны поверхности равных фаз в направлении, заданном углами θ и α. Центр кривизны поверхности - точка математически вполне определенная; она, действительно, представляет собой центр сферы, совпадающей с поверхностью равных фаз в точке, определенной направлением, заданным углами θ и α.

Может оказаться, что поверхность равных фаз волн, излученных антенной в данном направлении, вообще не имеет центра кривизны (рис.13), т. е. - ее кривизна различна при измерении в различных сечениях. В этом случае говорят, что антенна обладает астигматизмом. Для астигматических антенн можно говорить о частичных фазовых центрах, полученных для линий равных фаз, лежащих в той или иной плоскости, секущей поверхность равных фаз. Термин «частичный фазовый центр» заимствован из оптики при использовании аналогии с частичным фокусом систем, лучи которых не сходятся в одной точке - фокусе.

Рисунок 13 – Вид поверхности равных фаз при наличии астигматизма

Поляризационная характеристика (ПХ). Поле в дальней зоне антенны характеризуется поляризацией, т.е. характером изменения направления вектора Е во времени.

В плоскости, нормальной к направлению распространения ЭМВ, за период частоты конец вектора Е описывает эллипс, который принято называть поляризационным эллипсом (рис.14). Данный эллипс характеризуется 3-мя параметрами: коэффициентом эллиптичности К_Э, углом наклона большой полуоси и направлением вращения вектора Е.

Рисунок 14 – Поляризационный эллипс на плоскости по нормали распространения волны

Коэффициентом эллиптичности называют отношение малой к большой полуоси эллипса

, (16)

где Е_мин – минимальное, а Е_макс – максимальное значение напряженности электрического поля, а и b – большая и малая полуоси эллипса.

Видно, что К_Э изменяется в пределах от 0 до 1. Значение К_Э=0 соответствует линейной поляризации, а К_Э=1 – круговой поляризации. При всех остальных значениях К_Э поляризация будет эллиптичной. В некоторых случаях приходится учитывать направление вращения вектора , при этом можно соответственно различить левостороннюю и правостороннюю поляризацию.

Т.о ., зависимость параметров поляризационного эллипса от направления называют ПХ.

Излучаемая мощность. Излучаемая мощность – это полная мощность, которую излучает антенна в пространство, определяемая путем интегрирования плотности потока мощности П по поверхности сферы S произвольного радиуса, окружающей антенну

. (17)

Коэффициент направленного действия (КНД). КНД называется величина выигрыша в плотности потока мощности либо в излучаемой мощности, который дает антенна направленного действия по сравнению с антенной ненаправленного действия.

(18)

Коэффициент полезного действия (КПД). КПД антенны называется отношение мощности излучения антенны к мощности, подводимой к ее входу.

. (19)

Коэффициент усиления (КУ). КУ характеризует величину реального выигрыша по мощности, который дает антенна направленного излучения, по сравнению с ненаправленной антенной. Численно его можно найти

. (20)

Входное сопротивление. Входное сопротивление антенны – это сопротивление, на которое нагружена линия передачи, питающая антенну.

. (21)

Сопротивление излучения. Сопротивлением излучения называется такое активное сопротивление, которое как бы присутствует в антенне и на котором рассеивается мощность, излучаемая антенной в пространство.

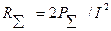. (22)

Действующая длина (высота) антенны. Действующая длина антенны – это длина некоторой линейной антенны с равномерным распределением тока, на которую нужно умножить амплитуду тока на клеммах, чтобы получить площадь тока реальной антенны.

, (23)

где – амплитуда тока в пучности.

Данный параметр поясним с помощью рис.15.

Рис. 15. К пояснению действующей длины (высоты) антенны

Частотный диапазон. Частотный диапазон характеризуется полосой пропускания – т.е. полосой частот, в пределах которой параметры антенны без ее перестройки не выходят за пределы, установленные техническими условиями, таким образом

ΔF=f_max - f_min. (24)

Иногда можно встретить понятие коэффициента перекрытия – это отношение граничных частот диапазона

К_П = f_max / f_min. (25)

В зависимости от значения К_П различают узкополосные (К_П ≤1,1) и широкополосные (К_П ≥3) антенны.

Заключительная часть. Преподаватель отвечает на вопросы курсантов, отмечает работу курсантов на лекции и дает задание на самостоятельную подготовку – изучить и законспектировать типовые структурные схемы радиосистем.

Подготовил:

доцент кафедры ТКОС, к.ф.-м. н. В.А. Мельник