сумма квадратов значений фактической ошибки модели должна быть минимальной.

Иными словами, найденные с помощью МНК оценки a ₀, a ₁,..., a_n, обеспечивают минимум следующей квадратичной формы на множестве всех других комбинаций значений таких оценок:

где e_t – значение фактической ошибки модели в момент t =1,2,..., Т, полученное после подстановки в выражение (1.2) вместо неизвестных истинных значений параметров a ₀, a ₁,..., a_n их оценок a ₀, a ₁,..., a_n.

Оптимальные по данному критерию значения оценок в этом случае могут быть найдены путем решения следующей системы так называемых “нормальных” уравнений, вытекающей из условия равенства нулю частных производных функции s ²(a ₀, a ₁,..., a_n) по своим параметрам в точке минимума:

В системе (2.3) неизвестными являются оценки параметров a ₀, a ₁,..., a_n, а ее известные коэффициенты сформированы на основе исходных данных и представлены в виде следующих сумм: i, j =1,2,..., п. Решения, получаемые на основе развернутой формы системы (2.3), достаточно громоздки, и поэтому в дальнейшем в математических выкладках общего характера будем использовать векторно-матричную форму представления ее составляющих.

Векторно-матричная форма записи линейной эконометрической модели (1.2) имеет следующий вид:

у = Х × a + e, (2.4)

где у – вектор-столбец, состоящий из Т компонент; Х – матрица размера Т ´(п +1) (если в модели присутствует “свободный” коэффициент a ₀); a =(a ₀, a ₁,..., a_n)¢– вектор-столбец параметров, состоящий из п +1-й компоненты; e – вектор-стобец ошибки модели, состоящий, как и вектор у, из Т компонент.

Соответственно векторно-матричный вариант модели, в котором вместо неизвестных истинных коэффициентов a и ошибок e используются их оценки, т. е. вектора а и е, запишем в следующем виде:

у = Х × а + е, (2.5)

где а =(а ₀, а ₁,..., а_n)¢, е =(е ₁, е ₂,..., е_Т)¢– вектора значений оценок коэффициентов линейной эконометрической модели и значений ее фактической ошибки соответственно.

Сумму квадратов значений ошибки s ² можем представить в виде скалярного произведения вектора-строки е ¢на вектор-столбец е. Проводя несложные преобразования с учетом правил произведения векторов и матриц, получим следующий результат:

s ² =(е ¢, е)=(у – Х × a)¢(у – Х × a)= у ¢ у – a ¢ Х ¢ у – у ¢ Хa + a ¢ Х ¢ Хa =

= у ¢ у –2 a ¢ Х ¢ у + a ¢ Х ¢ Хa. (2.6)

При проведении преобразований учитывалось правило транспонирования векторно-матричного произведения (z × W)¢=(W ¢ × z ¢).

Условие (2.3) в векторной форме записи приобретает следующий вид:

¶ s ²/¶ a = 0. (2.7)

Заметим, что в выражении (2.7) операция дифференцирования осуществляется по вектору.

С учетом выражения (2.6) уравнение (2.7) приводится к следующему виду:

¶ s ²/¶ a =¶(у ¢ у –2 a ¢ Х ¢ у + a ¢ Х ¢ Хa)/¶ a =–2 Х ¢ у +2 Х ¢ Хa = 0

или

Х ¢ Хa = Х ¢ у.

a =(Х ¢ Х)^–1× Х ¢ у. (2.8)

Все переменные в правой части выражения (2.8) являются известными – это исходные данные, сведенные в матрицу Х и вектор у.

Практика:

Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК).

МНК позволяет получить такие оценки параметров a и b, при которых сумма квадратов отклонений фактических значений результативного признака y от расчетных (теоретических) минимальна:

Для того чтобы найти минимум функции, надо вычислить частные производные по каждому из параметров a и b и приравнять их к нулю. Тогда мы получаем следующую систему нормальных уравнений для оценки параметров a и b

Решая систему нормальных уравнений либо методом последовательного исключения переменных, либо методом определителей, найдем искомые оценки параметров a и b. Можно воспользоваться следующими формулами для a и b:

Эта формула получена из первого уравнения системы, если все его члены разделить на n:

, где cov(x,y) — ковариация признаков; σх2— дисперсия признака х. Поскольку , получим следующую формулу расчета оценки параметра b

Таким образом:

Свойства оценок МНК

Свойство несмещенностиоценок состоит в том, что математическое ожидание оценки должно быть равно истинному значению параметра.

Свойство состоятельностиоценок состоит в том, что с увеличением наблюдений оценка становится более надежной в вероятностном смысле.

Оценка называется эффективной, если она имеет минимальную дисперсию по сравнению с любыми другими оценками этого параметра в классе выбранных процедур.

Методы оценивания линейной модели множественной регрессии в Excel.

Модель множественной регрессии имеет вид:

Построение множественной линейной регрессии в MS EXСЕL выполняется так же, как и в случае парной регрессии двумя способами: с помощью функции ЛИНЕЙН и через Сервис, Анализ данных, Регрессия.

В первом случае мы выделяли на определенном шаге 5 строк и 2 столбца для того, чтобы поместить туда выходные параметры (массивы) регрессии. Если для множественной регрессии количест­во факторов равно m, то нужно соответственно выделять для вы­ходных значений 5 строк и (m+1) столбцов. Заметим, что в первой строке вычисленные коэффициенты регрессии стоят в следующей очередности: b_k, bk-1, --, Ь₂, b₁, b₀.

Для второго способа через Сервис, Анализ данных. Регрес­сия все делается так же, как в случае парной регреcсии. Только в качестве входного интервала X, нужно выделить весь массив дан­ных соответствующих факторам X₁, Х₂,.... Х_k.

Применяется модель наименьших квадратов, если выполняется 4 условия теоремы Гаусса-Маркова:

1. Проверка качества модели

Находим Fкрит. через функцию FРАСПОБР (доверительный интервал 5%, степень свободы 1 = 1, степень свободы 2 = число степеней свободы при использовании функции Линейн). Fкрит сравниваем с числом Фишера (который мы также нашли через функцию линейн(первый столбец, 4 строка)).

2. Проверка качества коэффициентов.

Находим числа Стьюдента путем деления строки коэффициентов на строку ошибок коэффициентов. Находим tкрит. Через функцию СТЬЮДРАСПРОБР (вероятность 5%, степень свободы из функции Линейн (2 столбец, 4 строка)). Сравниваем найденные величины. Коэффициенты являются статистически значимыми, если числа Стьюдента больше tкрит.

2.2.2. Свойства оценок МНК

Рассмотрим основные условия, при которых оценки коэффициентов линейной эконометрической модели, во-первых, могут быть в принципе найдены, а, во-вторых, их “качество” будет “достаточно высоким”, что является определенным свидетельством и достаточного качества построенной модели.

Как было отмечено в разделе 1.5, “качество” оценок, их свойства тесно связаны со “статистической” трактовкой исходных данных и, в первую очередь, независимых переменных. Рассмотрим сначала случай, когда измеренные (наблюдаемые) значения независимых факторов трактуются как детерминированные (неслучайные) величины.

2.2. Особенности проверки качества оценок МНК

Проверка условий, выполнение которых свидетельствует о “высоком” качестве полученных оценок параметров эконометрической модели (а, следовательно, в значительной степени и самой модели), на практике обычно осуществляется с использованием ряда процедур и критериев, на основе исходной и новой, полученной после построения модели, информации. К исходной информации относятся наблюдаемые (измеренные) значения зависимой и независимых переменных y_t и х_it соответственно. Новую информацию составляют значения 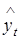, найденные оценки параметров a_i, соответствующие им фактические значения ошибки е_t, а также ковариационные матрицы оценок и ошибок (в последнем случае возможно только дисперсии), i =0, 1,..., п; t =1, 2,..., Т. Иными словами, значение Т при проверке предполагается конечным.

При этом следует иметь в виду, что новая информация обычно рассматривается как некоторая оценка (заменитель) истинных (но неизвестных) значений соответствующих характеристик. В этой связи совпадение свойств оценок с предполагаемыми теорией априорными свойствами соответствующих характеристик (часто, но не всегда) является определенной гарантией качества модели (оценок ее параметров). Особенно важную роль в определении качества модели играют значения ее фактической ошибки е_t, t =1, 2,..., Т; соответствующие полученным оценкам ее параметров.