Неравенство Рао – Крамера.
Замечание. “ Почти всюду по y “ означает: для всех y, за исключением, может быть, множества точек меры 0. Пусть, кроме того, выполнено условие
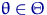Тогда справедливо Неравенство Рао – Крамера. Для любой несмещенной оценки
| 41. Эффективные оценки:
Определение
Оценка  называется эффективной в классе несмещенных оценок, если ее дисперсия меньше (не больше) дисперсий всех других оценок в этом классе. То есть для любой  , для любого 
Сформулируем очевидное следствие из неравенства Рао – Крамера.
Следствие.
Если семейство распределений  удовлетворяет условиям неравенства Рао-Крамера, и оценка  такова, что в неравенстве Рао – Крамера достигается равенство:
то оценка  эффективна в классе несмещенных оценок.
.
Пример 5.
Пусть  ,  ,  – выборка объема  из нормального распределения  , где  ,  . Проверим, является ли оценка  эффективной.
Найдем информацию Фишера относительно параметра  (считая, что имеется один неизвестный параметр – ).
Тогда 
Итак,  . Найдем дисперсию оценки  .
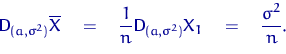Далее, сравнивая левую и правую части в неравенстве Рао – Крамера, получаем равенство:
То есть оценка  эффективна (обладает наименьшей дисперсией среди несмещенных оценок).
Пример 6.
Пусть , , – выборка объема из показательного распределения  с параметром 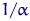 , где  . Проверим, является ли оценка  эффективной.
Найдем информацию Фишера относительно параметра 
 
Плотность данного показательного распределения имеет вид:
Тогда
Итак,  . Найдем дисперсию оценки .
 .
Подставив дисперсию и информацию Фишера в неравенство Рао-Крамера, получаем равенство:
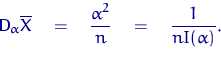То есть оценка  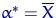– эффективная оценка параметра .
|
42.Интервально оценивание. Общий принцип построения доверительных интервалов.
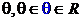Пусть, как обычно, имеется выборка  из распределения с неизвестным параметром  . До сих пор мы занимались «точечным оцениванием» неизвестного параметра — находили число («оценку»), способную, в некотором смысле, заменить параметр.
Существует другой подход к оцениванию, при котором мы указываем интервал, накрывающий параметр с заданной наперед вероятностью. Такой подход называется «интервальным оцениванием». Сразу заметим: чем больше уверенность в том, что параметр лежит в интервале, тем шире интервал. Так что искать диапазон, в котором  лежит с вероятностью 1, бессмысленно — это вся область  .
Определение.
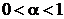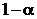Пусть  . Интервал  называется доверительным интервалом для параметра с уровнем доверия  , если для любого
Замечание.
Неравенство  обычно соответствует дискретным распределениям, когда нельзя обойтись равенством: например, для  при любом 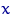 равенство  невозможно, а неравенство имеет смысл:
Прежде чем рассматривать регулярные способы построения доверительных интервалов, разберем пример. Начнем с нормального распределения как с наиболее важного и часто встречающегося.
Пример 1.
Пусть , , — выборка объема из нормального распределения , где — неизвестный параметр, а известно. Требуется построить ДИ для параметра c уровнем доверия .
Нормальное распределение устойчиво по суммированию. (убедиться самостоятельно):
Пусть  ,  имеют нормальное распределение  , и эти случайные величины независимы. Тогда  имеет нормальное распределение с параметрами
 ; 
Поэтому
Итак, величина  имеет стандартное нормальное распределение.
По заданному  найдем число  такое, что  .
Определение.
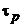Пусть распределение  с функцией распределения  непрерывно. Число  называется квантилью порядка p распределения , если  р. Если функция монотонна, квантиль определяется единственным образом.
Если число  — квантиль порядка  стандартного нормального распределения, то
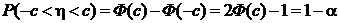Или  .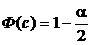
Итак,  , и  (квантили стандартного нормального распределения).
Разрешив неравенство
Можно подставить
Итак, искомый доверительный интервал с уровнем доверия
Мы построили доверительный интервал для параметра
имеющую при любом
Поиск по сайту©2015-2025 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование. Дата создания страницы: 2018-01-27 Нарушение авторских прав и Нарушение персональных данных |
Поиск по сайту: Читайте также: Деталирование сборочного чертежа Когда производственнику особенно важно наличие гибких производственных мощностей? Собственные движения и пространственные скорости звезд |
существует, положительна и непрерывна по 
, дисперсия которой 
ограничена на любом замкнутой области 
, справедливо неравенство
артного нормального распределения и квантили.
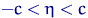относительно 
имеет вид
нормального распределения при известном 
. Для этого мы рассмотрели функцию от выборки и неизвестного параметра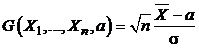 
,