Найти функцию 
, распределение которой G не зависит от параметра 
. Необходимо, чтобы была обратима по при любом фиксированном 
2. Пусть числа 
и 
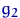— квантили распределения 
такие, что
3. Разрешив неравенство 
относительно (если это возможно), получим ДИ.
Замечание.
Часто в качестве и 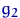берут квантили порядка 
и 
распределения 
. Но, вообще говоря, квантили следует выбирать так, чтобы получить ДИ наименьшей длины.
Можно построить доверительный интервал для параметра 
нормального распределения при неизвестном 
. Можно
- построить ДИ для 
при известном ,
- построить ДИ для при неизвестном ..
Такой особый интерес к нормальному распределению связан с центральной предельной теоремой — по этой теореме все в на свете нормально или стремится к нормальному. Поэтому рассмотрим распределения, связанными с нормальным распределением и их свойства.
независимых стандартных нормальных случайных величин называют распределением «хи-квадрат» с 
.
На графике ниже изображены плотности распределения 
при 
случайную величину с распределением 
-распределения:
1.
Устойчивость по суммированию.
Пусть случайная величина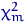 
имеет распределение 
, причем эти случайные величины независимы. Тогда их сумма 
имеет распределение 
.
Доказательство. Пусть 
, 
независимы и имеют стандартное
нормальное распределение. Тогда
а их сумма — как 
, т.е. имеет распределение 
.
2.
Моменты распределения 
Доказательство. Пусть 
независимы и имеют стандартное
нормальное распределение. Тогда
Поэтому
Следствие.
Если 
независимы и имеют нормальное распределение 
, то
имеет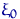 
, 
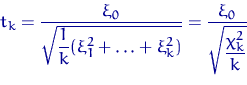называют распределением Стьюдента с 
.
Свойства распределения Стьюдента:
1.
Симметричность.
Если случайная величина 
имеет распределение Стьюдента 
имеет такое же распределение. (Сразу следует из определения).
2. Mtk=0; D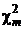 
— распределение 
называют распределением Фишера с 
степенями свободы и обозначают 
.
Свойства распределения Фишера
1.
Если 
имеет распределение Фишера 
имеет распределение Фишера 
. Следует из определения.
2. M. 
— выборка из 
. Пусть 
— ортогональная матрица 
, т.е.
Лемма Фишера.
Пусть вектор 
состоит из независимых случайных величин со стандартным нормальным распределением, 
. Тогда для любого 
и имеет 
с 
степенями свободы.
Доказательство. Ортогональное преобразование не меняет нормы векторов, поэтому нормы векторов 
совпадают:
Поэтому
Случайные величины 
, 
получены из 
с помощью ортогонального преобразования, поэтому независимы и имеют стандартное нормальное распределение, и 
имеет распределение 
.
Основное следствие леммы Фишера.
Вспомним, что
Если 
, 
независимы и имеют нормальное распределение 
имеет стандартное нормальное распределение (очевидно);
имеет 
степенью свободы;
Случайные величины 
и 
независимы.
Доказательство
2.
где 
имеют стандартное нормальное распределение, и 
.
В обозначениях леммы Фишера.
Мы обозначили через 
Чтобы применить лемму Фишера, нужно найти ортогональную матрицу 
. Так как норма этого вектора — единица, его можно дополнить до ортогональной матрицы. Тогда 
и будет первой координатой вектора 
не зависит от 
имеет стандартное нормальное распределение (для 
имеет распределение 
(для 
имеет распределение 
(для 
имеет распределение 
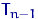(для 
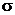. Этот интервал мы уже построили в $1:
2.
Для 
при известном 
Пусть 
и 
— квантили распределения 
=
, где
3.
Для 
Пусть 
и 
— квантили распределения 
4.
Для 
Пусть 
и 
— квантили распределения 
. Тогда
