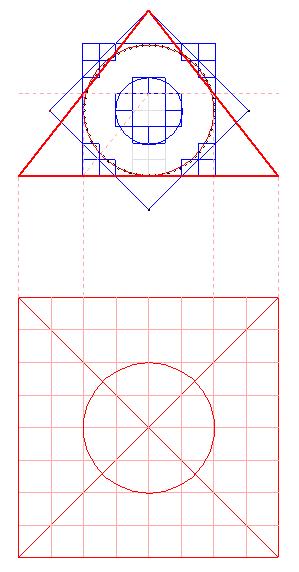
Если взять наш квадрат 8х8, то половина отрезка KD будет радиусом окружности с длиной равной периметру квадрата. Если его поставить в центре, то получится великая и могучая пирамида IGH.
Второе (западное) колесо указывает на сторону основания подобной пирамиды, но с целочисленной высотой, равной 10.

Т.е. "колеса" (намекая своими правильными окружностями на Pi и на длину окружностей) указывают с одной стороны на радиус окружности (KD) с модульной длиной 64, а с другой стороны указывают на 1/8 длины окружности (BE), модульный радиус которой равен 10 (BA). Они указывают на два подобных треугольника, на два параллельных пути решения задачи! И на обратимость зависимости периметра и радиуса.
Говорить о случайном совпадении таких математических зависимостей трудно.
Но вот что любопытно:
32-угольник или 64-угольник мы можем построить соединив центр с разметочными точками на окружностях. В построении он не учавствует, но он описывает логику дальнейшего движения. Он всего лишь показывает начало итерационного процесса, намекя на схему нахождения окружности с длиной кратной единице.
Маркировочные квадратики объясняют схему построения восьмиугольника со стороной равной 1. А дальше - бесконечный процесс.
(Кроме того, они таким же образом же объясняют механизм определения площади круга. Именно механизм бесконечного процесса стремящегося к уточнению Pi. Выложу позже.)
Величину Pi вычислить невозможно, и здесь дается не конкретное построение, дающее конечный результат, а описываются начала и направление повторяемых построений ведущих к уточнению иррациональной величины.
Мы можем еще построить 128-угольник и получить еще более точное значение.
До Архимеда Pi пытались вычислить и представить в виде рационального числа. Архимед в III в днэ сделал вывод, что отношение любой окружности к ее диаметру меньше чем 3 1/7 и больше 3 10/71.
Этот вывод был основан на последовательном вычислении периметров вписанных и описанных многоугольников с количеством сторон равным 6, 12, 24, 48 и 96.
Практически этим и был создан алгоритм последовательного приближения к числу Pi, к его приближенному значению. Но пирамида уже стояла, символизируя собой и загадочной своей вершиной-пирамидоном бесконечность, в том числе и этого процесса.
Иными словами, это не просто разбивочный чертеж какого-то сооружения, и далеко не декоративное творчество местных жителей. Это именно иллюстрация, пособие по геометрии и квадратуре круга. Ни формул, ни цифр, ни текстов. Все изображено языком геометрии, композиционной логикой, внутренней динамикой, приводящей к необходимым выводам. Даже в самых древних математических папирусах присутствуют надписи, пояснения и привычные нам со школы методы изложения гепотиз, теорем и их доказательств. Но здесь все упаковано в геометрию.. Потрясающе!
Кому, спрашивается, понадобилось рисовать схему определения Pi, величиной в сотни метров, если даже с самолета ее трудно рассмотреть, и то при подходящем освещении?

Кроме того, с архимедовских времен известно, что площадь круга равна треугольнику с катетами равными длине окружности и радиусу. То есть, площадь тр ABO равна площади круга R4. Соответственно и для других окружностей то же.
Получаем неплохой прибор, с которым можно выполнять преобразования на основе числа Pi, с определенной точностью. Например построить окружность с нужным периметром, или по радиусу определить длину окружности:
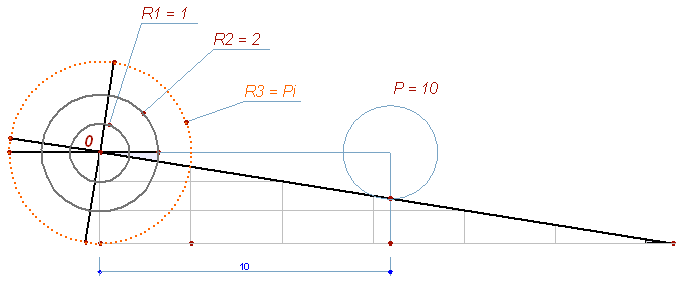
Не такой ли волшебный угол предлагают нам построить данным фрагментом:

На некоторых фрагментах видно, что сектор (1/4) окружности R3 делится не на 8, а на 9 частей! это уже перевод измерения угловых величин с долей Pi (радианы) в градусы, разделив окружность на 36 частей.
(что поделаешь с этим образным мышлением..)
Вписав теперь сечение Великой пирамиды в наш чертеж, получаем удивительные такие совпадения...
Модульный квадрат получился в реальности 14.65 метра. Что равно 28 кубитам, если половина основания считать равным 220 кубитов.
"Колеса" я отзеркалил относительно оси, чтобы нагляднее было, потому, что угол OE имеет угол важный. А вторая группа окружностей похоже только для построений использовалась.
(Оранжевым отметил интересные моменты)
 +
+
Наша модульная сетка и система пропорций на основе квадратов Qa и Qb очень пришлись по вкусу надменному сооружению.
1. Как красиво вписалась "камера царя" в центральный квадрат, где у нас лучики лучезарные..
2. Как красиво сидит "камера царицы", поднявшись на полтора модуля от уровня земли..
3. Как здорово совпадает угол наклона большой галереи (и нисходящего пассажа, он почти такой же)
Там же из точки Е "странная" линия "колеса" указывает на их пересечение.
4. Как забавно сидит самая нижняя подземная камера..
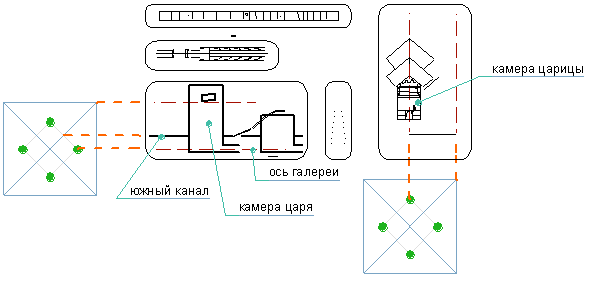
5. Как удачно совпало прохождение южного (левого) канала из "камеры царя". Как-то он так по диагонали модульных квадратов..
Выходы обоих каналов тоже как-то удачно..
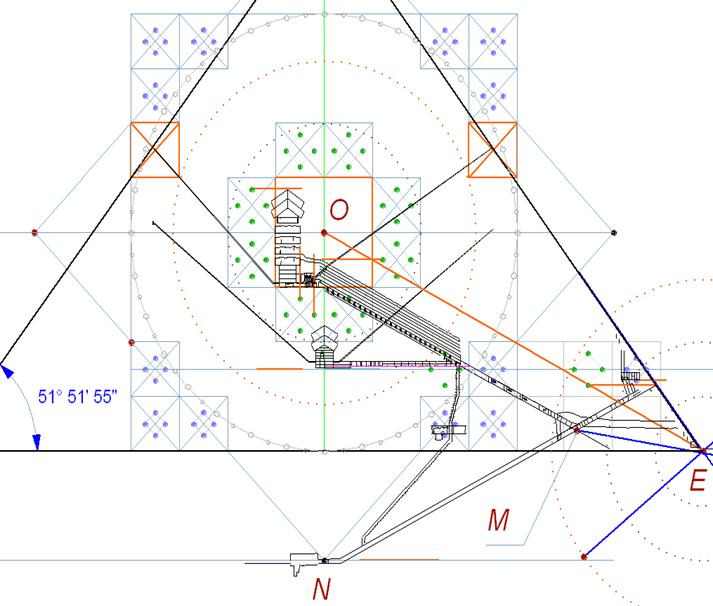
7. Даже размеры конструкций (5 перекрытий) "камеры царя" и тамбура входного..
Дальше на план посмотрим:
...
Или древним инкам было известно устройство великой "сокровищницы" и они разрабатывали план похищения, или "одно из двух"..
...
Нда..
Может кто-нибудь объяснит мне, где я ошибаюсь?
Или - на плато Пальпа, недалеко от местечка Наска, что в Перу, вычерчен проект Великой пирамиды..
Рядом с геоглифом, похоже на возвышенности, откуда его лучше наблюдать заметны три буковки "JMP" (похоже P последняя).
Явно следы современного гуманоида.

Возле центра трех окружностей справа заметен странный символ. Располагается на параллельных линиях, которые проходят через центральный квадрат 2х2. Правым нижним углом указывает на точку пересечения наклонного диаметра окружностей и нижней линии.
Конечно, может оказаться, что это свежие следы. Линии правда характерно очень проходят по чертежу. Вообще, кроме явно выделенных линий геоглифа там проходят иногда едва заметные прямые линн, не взирая на рельеф. Такое ощущение что это линии построения, "карандашные". И это подтверждается (попозже выложу).
Символы видны и с других ракурсов. Тут я сделал негатив, вроде заметнее выглядит. Такой вот "Пi". хм..

Технические детальки
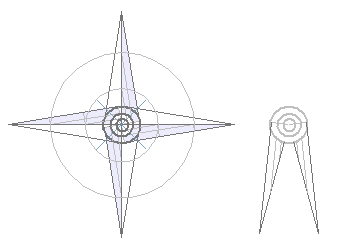
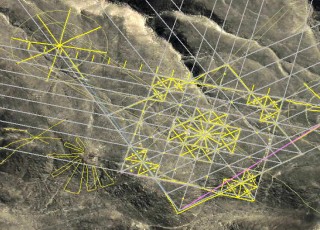
Геоглиф состоит из трех частей: в центре "звезда" из двух квадратов, и два "колеса" - группы из трех окружностей в одном центре и по четыре диаметра.
 (900x359, 73k)
(900x359, 73k)
рис 1
На фото с разных ракурсов заметны неточности построения линий ячеек, диагональных сегментов, окружности, тоже, далеко не идеально выстроены. Погрешность в 1-2 толщины линии не позволяет судить о геоглифе, как о точном чертеже точном. Я стараюсь его рассматривать как схематический рисунок, несущий логическую информацию в элементах и их взаимном расположении. Но без приближенного знания расположения "колес" и ориентации их диаметров какие-то теории, конечно, трудно строить.

рис 2
Если "звезда" не вызывает сомнений относительно правильности прочтения геометрии, то расположение окружностей может трактоваться по разному.
Рисунок расположен на относительно ровной площадке в скалистой местности. Немного поднимается правый верхний угол звезды, левый верхний - напротив завален в овраг.
Колеса относительно центральной части тоже слегка приподняты. (Ну такие уж термины в отсутсвие топосъемки).
Линии геоглифа представлят собой проекции вертикальных плоскостей, поэтому судить о рельефе можно по снимкам с разных точек. Снимки есть с юга, с запада, и с севера.
На рисунке нанесена квадратная сетка и это облегчает задачку по построению плоского перспективного чертежа.
Что я делал.
На снимках, где расположение основания квадрата почти параллельно линии горизонта, величина ячеек по горизонтальной оси практически не искажается. Подложив в чертежную программу, я могу накладывать векторные линии по пикселам изображения, с точностью настолько, насколько его качество позволяет. Выбирая наиболее характерные точки квадратов, с учетом падения по рельефу я обводил несколько линий квадратов. Затем попарно выбирая их и находя точку их пересечения, я получаю несколько точек перспективного схода параллельных прямых на линии горизонта. Аппроксимирую (на глаз естественно) и подгоняю остальные линии. Таким образом получается выполнить приблизительную квадратную решетку в перспективе, но уже находящуюся в усредненной плоскости.

рис 3
Выравниваю размеры ячеек, с учетом перспективного искажения.

рис 4
По восточному "колесу" у меня сомнений нет. Оно находится на расстоянии около 10.2 модуля от вертикальной оси и на одну единицу ниже горизонтальной. Указывает на радиус окружности с периметром 64.
 (706х508, 90.9Kb)
(706х508, 90.9Kb)
рис 5
По правому колесу некоторые неясности, но мне кажется непринципиальные на этом этапе.
В комментариях bob_1 был прав, центр не лежит на оси Х как ни крути. И сдвижка вверх заметно больше любых других погрешностей. И как видно с разных ракурсов не из-за рельефа.
Изучил этот кусок поподробнее.
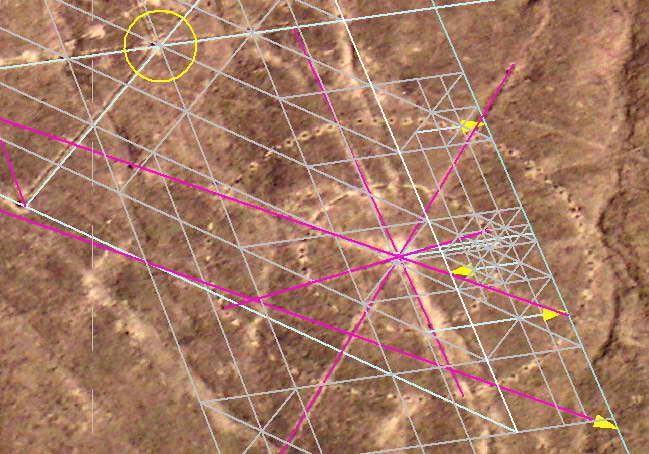
рис 6
(кружком показал крупную погрешность второй самой левой ячейки с неизу. И от нее диагональ к вершине повернутого квадрата тоже сбоит).
Ось Х - белая. С учетом рельефа по Х центр попадает на -7.5 единицы от по Y близко к 0.5. Расстройство конечно, но удалось убедиться еще раз, что
западное "колесо" указыавет на угол наклона его диаметров. И этот угол очень близок к 52°. Луч явно проходит через вершину А. Прохождение луча и диаметров по модульным клеткам старался еще раз проверить на чертеже (стрелки) желтые.
Кроме того, на геоглифе есть тонкие линии ("линии построения"). Рядом с наклонным диаметром (западнее)проходит одна такая. На рис 6 она фиолетовая нижняя. и на рис 4 видно ее продолжение.
На следующем зеленая (e)

рис 7
Там много таких линий, они явно прямые безупречно, и по ним тоже легко сверять некоторые моменты.
Эта линия (e) оказалась параллельной наклонному лучу нашего колеса. Кроме того, часть явно заметных линий сошлись в одну точку. И как оказалось на вертикали от центра восточного колеса. О назначении линий b, c-c, d ничего не могу сказать, но то что они сходятся вместе с линией (a) (от центра левого колеса) это забавно.. Может и действительно линии построения. Дело в том, что линия (е) попадает в точно в центр восточного колеса если его перенести на западную сторону.
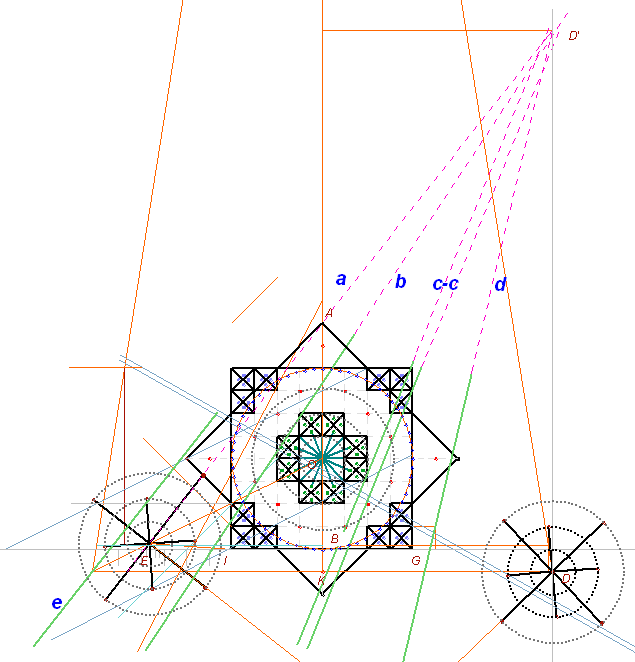
рис 8
Может быть это все и совпадения, но слишком уж их тут много.
Я считаю, левое колесо фиксирует именно луч AE под углом к оси X именно близкий к 52 градусам.
Именно этот угол и является конечным результатом приближенного вычисления длины окружности. Чем точнее будет выщитан радиус окружности KD, тем ближе будет угол к 51°51'14".
Способов построения точки E и луча AE множество, если есть пи-треугольник KDX.
Какую именно длину периметра указывает приподнятая точка E, пока не ясно. (но предположения есть))
Резюмируем вобщем:
- Звезда задает механизм построения, и всем своим видом призывает решить задачку нахождения периметра окружности и построения квадрата с таким же периметром (и наоборот).
- Правое колесо указывает (по оси Х) на радиус KD окружности с периметром 64 (ось Y).
- Левое колесо, наоборот, по Х откладывает длину окружности (точнее 1/8), а по Y получаем радиус. (угол 51°51'14") (1/8 периметра - есть половина стороны квадрата или сторона восьмиугольника)
приклею gif и ссылку на swf: https://kavalet.narod.ru/estrella/star_swf.html
Пирамида и чертеж
https://kavalet.narod.ru/
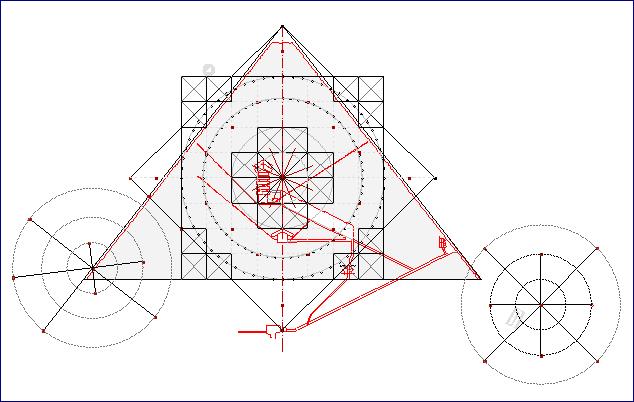
Собрал все и разложил по полочкам. Шумашедшая идея конечно, но слишком много соответствий. Единая композиционная логика и, как ни странно, единый стиль. Информвция из геоглифа раскручивается как китайский фейерверк.
Объяснить коротко и убедительно оказалось делом не простым, потому и извиняюсь.
Есть такая шутка старая, как тетушка обвиняла в суде архитектора за оскорбление личности.
"Стены в доме были стеклянными, а т.к. дом похож на аквариум, а значит он считает, что она - рыба."
Это я к тому, что вывести псевдологику можно, естественно, откуда угодно.
Поэтому я старался объяснить то, что может на первый взгляд показаться "притянутым за ухи". В принципе, доказать такое предположение, наверное невозможно, но попытаться сложить аргументы за и против - все таки можно.
Еще одна деталь по поводу угла в 51° 51' 14". (угол при котором в прямоугольном треугольнике один катет - радиус, а второй 1/8 длины окружности)
(угол соединяющий центр левых окружностей с вершиной звезды)
Геоглиф имеет особенность, которую можно рассматривать как "неточность":
большая окружность (R=4) звезды не касается сторон квадрата, в который она вписывается на первый взгляд.
 (686x400, 79 kb) (тут видны все 4 точки касания)
(686x400, 79 kb) (тут видны все 4 точки касания)
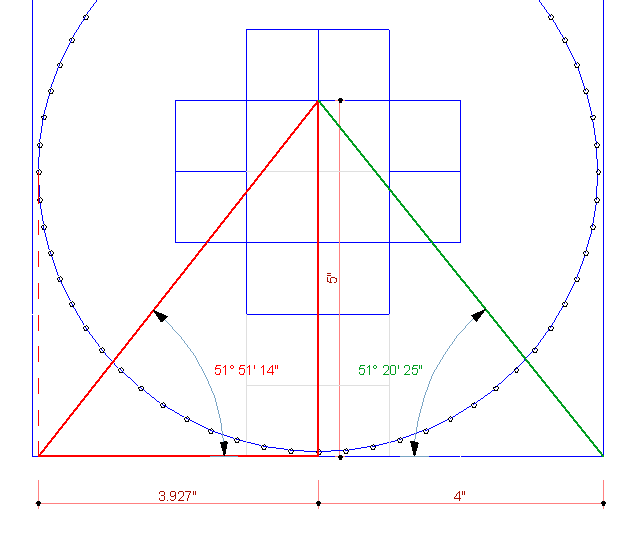
Справа, треугольник с зеленой диагональю, имеет катеты 4 и 5 ед, и угол 51° 20' 25", - чистое решение с позиции модульности.
Но если считать, что речь идет о длинах окружности, то величины катетов не могут быть кратными одной величине. Т.е. если высота - целочисленая, то основание - иррациональное. И в таком случае, радиус большой окружности указывает на иррациональную величину не случайно: такая окружность будет вписываться в квадрат со стороной 3.927... ед.
Таким образом, большая окружность будет принадлежать модульной сетке основания правильной пи-пирамиды с высотой в 10 ед.:
Т.е. то что она не вписывается - говорит о "легком" несоответствии величин высоты и основания треугольника (5 и 3.927..).
Т.е. высота разбивается на 10 частей и на высоте 5 ед. в сечение пирамиды вписывается точно эта окружность.
Т.е. в геоглифе левые окружности указывают на угол 51° 51' 14".
Большая окружность не касается сторон квадрата звезды потому, что:
- она относится к полярной системе, которая базируется на иррациональном основании пи-пирамиды.
- является еще одной подсказкой в том, как правильно прочесть чертеж.
Конечно, это может быть просто неточностью местных индейцев, развлекающихся рисованием на километровых пространствах в скалистой местности.
Ф. Питри в отчете об обследовании пирамид в Гизах, описывая потолочные своды "камеры царицы" (sec. 42), пишет о том, что длина потолочной балки по уклону равна 120 дюймам. А в глубь стены балка уходит еще на 121.6 дюйма (дырку пробил полковник Вайс до него). Питри делает вывод, что центр этим тяжести балки смещается в глубь стены и она начинает работать как консоль. Неплохо разбираясь в конструкциях египетских построек он слегка удивляется такому необычному подходу.
Я напомню примерно как работают обычные двухпролетные своды: 
Воспринимая нагрузку сверху, балки свода передают ее часть в виде распорных усилий на боковые подпирающие блоки.
Обычно в таких ситуациях требуются какие-то контрфорсные мероприятия. Внутри пирамиды этого добра хватает, те упереть балки в теле пирамиды есть во что.
Кроме того, Питри удивило еще и то, что аналогов решения сводов он не встречал.
В подробных официальных изданиях, описывающих архитектуру древнего Египта, двухпролетный свод трактуется как зачаточное состояние конструкторской мысли. Шуази, например, приводит такой свод из разгрузочной камеры пирамиды в Гизе, свод над "входом" из двух рядов балок в той же пирамиде и еще один из Дэйр-Эль-Бахри. Затем он приводит еще свод из трех клиньев в одной из гробниц в Гизе и пишет, что дальнейшего развития этот вид сводов у египтян не получил. Египтянам он не приглянулся.
Мне хочется тут немного рассмотреть "зачаточное" состояние конструкторской мысли.
Итак сводчатые клинья в камере царицы работают как консольные балки.
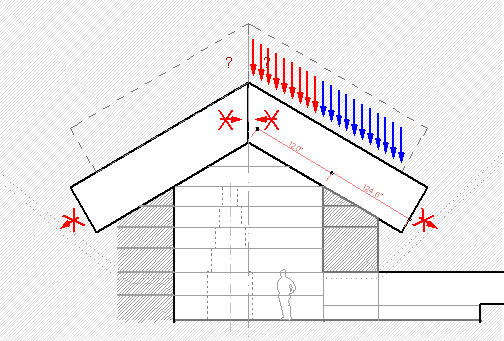
Тем самым уменьшив до минимума распорное усилие в стороны. Вся нагрузка от свода будет сосредоточена на краю стены, а дальние концы балки напротив - разгружаются.
 (так примерно работает консольная балка)
(так примерно работает консольная балка)
Теперь посмотрим сечение "камеры царицы" по шахтам, выходящим из камеры:

Блоки образующие каналы, взяты у RUDOLF GANTENBRINK
Он своим роботом тщательно изучил швы в каналах и, основываясь на этом изобразил раскладку блоков.
Но в своих чертежах он не учитывает длину блоков, замерянную Питри (? не ясно почему). И, полагая, что в камере обычный свод, нарисовал на своих схемах распорные усилия.
И тут самое интересное.
Обычный свод, разгоняя нагрузку в стороны, сдвигал бы блоки каналов, и между ними бы образовывались щели. Но находящиеся в "зачаточном состоянии" конструкторской мысли авторы постройки (к египтянам мало имеет отношения похоже) меняют способ разгрузки свода, и направляют нагрузку вертикально, на мощные стены камеры. Причем разгружая концы балок над блоками каналов.
Остается загруженным только один блок - с горизонтальным фрагментом канала.
И тут "зачаточная мысль" еще раз шевельнулась, и
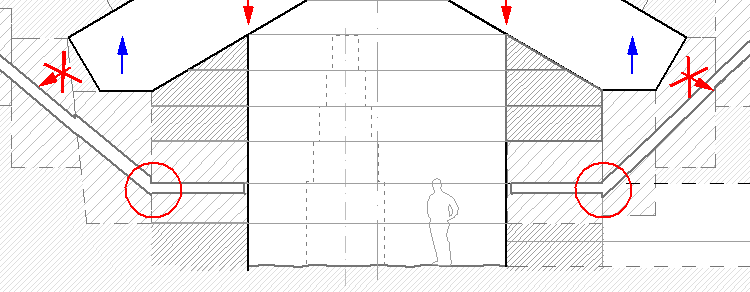
для компенсации вертикального смещения загруженных сводом стеновых блоков наклонные каналы сделаны с запасом высоты отверстия. Смещаясь вниз, горизонтальный участок не потеряет стыковку с отверстием соседнего блока. На мой взгляд, решение проблемы сохранения целостности канала при естественной усадке - весьма профессиональное.
Назначение каналов, правда, остается "той еще" загадкой "с дверцами". В оригинале они не были прорублены до конца и отделялись от пространства камеры тонкой перегородкой каменной стены. Одну пробил Диксон, другую Питри, не оставив подробного обследования выбитого фрагмента стены. Обнаружил Диксон пустоту посредством простукивания стены. Были там микроотверстия или нет уже никто не узнает.
https://www.egyptarchive.co.uk/html/great_pyramid_20.html
источник https://kavalet.livejournal.com/4089.html