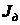ЛАБОРАТОРНАЯ РАБОТА 2М (задание 2)
ИЗУЧЕНИЕ ПОСТУПАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТЕЛ И ПРОВЕРКА ОСНОВНОГО ЗАКОНА ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТЕЛ НА МОДЕЛИ МАЯТНИКА ОБЕРБЕКА
В лабораторной работе на основе опытных данных определяются кинематические, динамические и энергетические характеристики тел при поступательном и вращательном движении и проверяются основной закон динамики вращательного движения тел и теорема Штейнера.
Описание установки
В лабораторной работе поступательное и вращательное движение тел изучается на установке, основной частью которой является модель маятника Обербека – крестообразный маятник. Схема установки приведена на рис. 2.1.

Рис. 2.1
Вращающейся частью установки (рис. 1,а) являются четыре одинаковых стержня 1, укрепленных на цилиндрическом диске 2 под прямым углом друг к другу (крестовина), и два шкива 3 и 4 различного диаметра  , жестко соединенные с диском 2.
, жестко соединенные с диском 2.
На стержнях находятся цилиндрические грузы 5 массой  , которые можно перемещать по стержням и с помощью винтов на них закреплять на выбранных расстояниях
, которые можно перемещать по стержням и с помощью винтов на них закреплять на выбранных расстояниях  на стержнях.
на стержнях.
Диск крестовины и шкивы насажены на общий стержень, закрепленный в подшипниках так, что вся эта система – маятник Обербека – может вращаться вокруг вертикальной оси  , перпендикулярной горизонтальной плоскости крестовины и проходящей через ось диска.
, перпендикулярной горизонтальной плоскости крестовины и проходящей через ось диска.
К шкивам прикрепляется нить 6. Нить перекидывается через блок 7, к свисающему свободному концу нити подвешивается груз 8 массой  .
.
Если, вращая маятник руками, намотать нить на шкив и поднять груз 8 на некоторую высоту  и отпустить маятник, то груз, опускаясь (падая), приводит всю систему в движение. При этом груз совершает поступательное движение, а маятник – вращательное.
и отпустить маятник, то груз, опускаясь (падая), приводит всю систему в движение. При этом груз совершает поступательное движение, а маятник – вращательное.
В установке предусмотрена возможность фиксации груза на выбранной высоте  с помощью электромагнита 9, расположенного в верхней части установки. Высота падения груза
с помощью электромагнита 9, расположенного в верхней части установки. Высота падения груза  измеряется по линейке 10, установленной в верхней части установки, на которой указано расстояние груза от столика установки 11.
измеряется по линейке 10, установленной в верхней части установки, на которой указано расстояние груза от столика установки 11.
Для измерения времени падения груза  используется цифровой секундомер. При нажатии кнопки секундомера «пуск» электромагнит автоматически отключается, и груз начинает опускаться, а секундомер начинает считать время. В место падения груза на столик 11 вмонтирован датчик 12, выключающий секундомер при ударе груза об это место столика установки.
используется цифровой секундомер. При нажатии кнопки секундомера «пуск» электромагнит автоматически отключается, и груз начинает опускаться, а секундомер начинает считать время. В место падения груза на столик 11 вмонтирован датчик 12, выключающий секундомер при ударе груза об это место столика установки.
Подвешивая грузы с разной массой и к разным шкивам, можно изменить момент сил, действующих на маятник, а передвигая цилиндрические грузы на стержнях, можно изменять момент инерции маятника.
Таким образом, установка позволяет измерить высоту падения (опускания) груза  и время падения
и время падения  , на основе которых при заданных значениях массы груза
, на основе которых при заданных значениях массы груза  и диаметра шкива
и диаметра шкива  можно определить кинематические, динамические и энергетические характеристики поступательного движения груза и вращательного движения маятника, принимая их равноускоренными.
можно определить кинематические, динамические и энергетические характеристики поступательного движения груза и вращательного движения маятника, принимая их равноускоренными.
Установка позволяет также проверить основной закон динамики вращательного движения
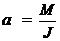
 (2.1)
(2.1)
т.е. прямо-пропорциональную зависимость углового ускорения маятника от момента сил  , действующих на тело:
, действующих на тело:
a ~ M (2.2)
при постоянном моменте инерции тела  , и обратно-пропорциональную зависимость углового ускорения
, и обратно-пропорциональную зависимость углового ускорения  от момента инерции
от момента инерции  тела:
тела:
 (2.3)
(2.3)
при постоянном моменте действующих сил  .
.
Задание2. Проверка зависимости углового ускорения
от момента инерции маятникаи зависимости момента инерции тела от расстояния до оси вращения (теоремы Штейнера)
Теория метода
Проверка зависимости углового ускорения от момента инерции маятника. Для проверки обратно-пропорциональной зависимости углового ускорения от момента
инерции маятника при постоянном моменте силы  (2.3) момент инерции маятника
(2.3) момент инерции маятника  изменяют, закрепляя цилиндрические грузы 5 на стержнях 1 на разных расстояниях
изменяют, закрепляя цилиндрические грузы 5 на стержнях 1 на разных расстояниях  от оси вращения.
от оси вращения.
Значения момента инерции маятника при разных положениях грузов 5 на стержнях находим по основному закону динамики вращательного движения
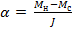 ,
,  . (2.4)
. (2.4)
Для этого при одном и том же шкиве 3 или 4, при одном и том же грузе 8 и при одной и той же высоте падения груза 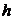 , но при различных расстояниях
, но при различных расстояниях  , измеряют время падения груза
, измеряют время падения груза  и вычисляют угловые ускорения и момент силы
и вычисляют угловые ускорения и момент силы  при различных
при различных  .
.
Расчеты показывают, что момент силы  от
от  и
и  зависит слабо. Поэтому, принимая за
зависит слабо. Поэтому, принимая за  среднее значение, можно допустить, что
среднее значение, можно допустить, что

где  – число выбранных расстояний
– число выбранных расстояний  (число вычисленных значений
(число вычисленных значений  ).
).
Пренебрегая зависимостью момента сил сопротивления 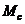 от скорости вращения маятника, можно принять
от скорости вращения маятника, можно принять
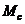 =
=  =
=  .
.
Тогда
 =
=  –
– 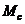 =
=  ;
;  (2.5)
(2.5)
Вычислив  и
и  при различных
при различных  и α и построив график зависимости α
и α и построив график зависимости α
от  , убеждаемся, что угловое ускорение действительно обратно пропорционально моменту инерции маятника.
, убеждаемся, что угловое ускорение действительно обратно пропорционально моменту инерции маятника.
Проверка зависимости момента инерции тела от расстояния до оси вращения (проверка теоремы Штейнера). Момент инерции системы тел равен сумме моментов инерции тел, составляющих систему тел. Поэтому момент инерции маятника  складывается из момента инерции крестовины (без грузов на стержнях)
складывается из момента инерции крестовины (без грузов на стержнях)  и момента инерции цилиндрических грузов 5 на стержнях
и момента инерции цилиндрических грузов 5 на стержнях  :
:
 =
=  +
+  .
.
Если грузы закреплены на одинаковых расстояниях  от оси крестовины (оси вращения), то моменты инерции
от оси крестовины (оси вращения), то моменты инерции 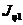 грузов 5 одинаковы. Тогда
грузов 5 одинаковы. Тогда
 = 4
= 4 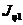 ;
;  =
=  + 4
+ 4 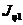 .
.
По теореме Штейнера момент инерции каждого груза 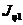 равен сумме момента инерции груза
равен сумме момента инерции груза  относительно оси, проходящей через центр инерции груза (через середину груза) перпендикулярно оси груза, и произведения массы груза
относительно оси, проходящей через центр инерции груза (через середину груза) перпендикулярно оси груза, и произведения массы груза  на квадрат расстояния
на квадрат расстояния  от оси вращения до центра инерции груза:
от оси вращения до центра инерции груза:
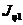 =
=  +
+ 
 . (2.8)
. (2.8)
Рассматривая груз как стержень, по таблице формул момента инерции находим
 =
= 

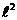 ,
,
где  – длина груза (высота цилиндрического груза).
– длина груза (высота цилиндрического груза).
Тогда
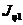 =
=  (
(
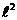 +
+  );
);  = 4
= 4 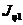 =
=  (
(
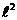 + 4
+ 4  );
);
 =
=  +
+  (
(
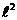 + 4
+ 4  ). (2.9)
). (2.9)
Таким образом, проверка формулы теоремы Штейнера для одного груза (2.8) сводится к проверке линейной зависимости момента инерции маятника  от
от  (2.9). Используя значения
(2.9). Используя значения  , вычисленные по формуле (2.7) и построив график зависимости
, вычисленные по формуле (2.7) и построив график зависимости  от
от  , можно убедиться в линейной зависимости
, можно убедиться в линейной зависимости  от
от  , т.е. в справедливости теоремы Штейнера.
, т.е. в справедливости теоремы Штейнера.
Определение момента инерции крестовины. График линейной зависимости момента инерции маятника  от квадрата расстояния грузов до оси вращения
от квадрата расстояния грузов до оси вращения  позволяет определить момент инерции крестовины
позволяет определить момент инерции крестовины  .
.
Отрезок  , отсекаемый графиком на оси
, отсекаемый графиком на оси  , соответствует расстоянию
, соответствует расстоянию  м и равен моменту инерции маятника, если бы центры грузов находились на оси вращения. Согласно (2.9) при
м и равен моменту инерции маятника, если бы центры грузов находились на оси вращения. Согласно (2.9) при  м
м
 =
=  + 4
+ 4  =
=  +
+ 

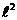 .
.
Отсюда
 =
=  -
- 

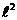 . (2.10)
. (2.10)
Определив  по графику, используя заданные значения
по графику, используя заданные значения  и
и  , можно найти момент инерции крестовины
, можно найти момент инерции крестовины  .
.
Порядок выполнения задания 2
1) Включить вилку шнура секундомера в розетку.
2) Установить дополнительный груз  на подвешиваемый груз с массой
на подвешиваемый груз с массой  (масса груза 8 будет равна
(масса груза 8 будет равна  ) и подвесить их к свободному концу нити.
) и подвесить их к свободному концу нити.
3) Перевести в положение «-» выключатель на задней панели секундомера; при этом секундомер должен показывать «00.0».
4) Освободив грузы 5 на стержнях с помощью винтов, установить их на рекомендованном расстоянии  от оси вращения.
от оси вращения.
5) Определить расстояние  от середины грузов 5 до центра диска 2.
от середины грузов 5 до центра диска 2.
6) Вращая маятник руками, намотать нить на один из шкивов и поднять груз  на рекомендованную высоту
на рекомендованную высоту 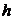 .
.
7) Нажав красную кнопку электромагнита, зафиксировать груз в этом положении.
8) По линейке 10 измерить высоту 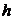 и записать в таблицу 3.1.
и записать в таблицу 3.1.
9) Нажав кнопку «пуск», включить секундомер.
10) Дождаться, когда груз 7 ударится об столик установки и закончится счет времени.
11) Показание секундомера – время падения груза  – записать в табл. 3.1.
– записать в табл. 3.1.
12) Выключить секундомер, поставив в положение «0» выключатель на задней панели секундомера.
13) При тех же  ,
,  ,
, 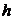 и
и  повторить пункты 4) …12) еще два раза (измерить время
повторить пункты 4) …12) еще два раза (измерить время  еще два раза).
еще два раза).
14) Выполнить пункты 3) … 13) при четырех других расстояниях  при тех же
при тех же  ,
, 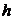 ,
,  .
.
15) Вынуть вилку шнура секундомера из розетки.
Вычисления к заданию 2
(результаты вычислений внести в таблицы 2.3.1, 2.3.2)
1) Вычислить среднее время падения груза  при различных расстояниях
при различных расстояниях  грузов на стержнях от оси вращения (табл. 2.3.1).
грузов на стержнях от оси вращения (табл. 2.3.1).
2) Вычислить угловое ускорение при всех выбранных  (см. задание 3,г к упражнению 1).
(см. задание 3,г к упражнению 1).
3) Используя выражение момента силы натяжения  , полученное в задании 6 к упражнению 1, вычислить
, полученное в задании 6 к упражнению 1, вычислить  при всех
при всех  .
.
4) Вычислить среднее значение момента силы натяжения  .
.
5) Используя основной закон динамики вращательного движения, выразить через  ,
, 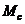 и
и  и вычислить момент инерции маятника
и вычислить момент инерции маятника  при всех расстояниях
при всех расстояниях  .
.
6) Вычислить значения  .
.
7) Построить график зависимости углового ускорения  от величины
от величины  и убедиться, что угловое ускорение при постоянном моменте сил, действующих на тело,
и убедиться, что угловое ускорение при постоянном моменте сил, действующих на тело,
действительно обратно пропорционально моменту инерции тела: 

 .
.
8) Для всех расстояний  вычислить
вычислить  .
.
9) Построить график зависимости момента инерции маятника  от
от  и убедиться в линейной зависимости момента инерции маятника от квадрата расстояния цилиндрических грузов 5 от оси вращения.
и убедиться в линейной зависимости момента инерции маятника от квадрата расстояния цилиндрических грузов 5 от оси вращения.
10) По графику зависимости  от
от  определить момент инерции маятника
определить момент инерции маятника  при
при  = 0 м, т.е. в случае, когда грузы 5 были бы расположены так, что ось вращения проходит через их центры масс перпендикулярно их оси.
= 0 м, т.е. в случае, когда грузы 5 были бы расположены так, что ось вращения проходит через их центры масс перпендикулярно их оси.
11) Выразить через момент инерции маятника  , массу грузов
, массу грузов  и длину
и длину  грузов 5 (получить формулу 2.10) и вычислить момент инерции крестовины
грузов 5 (получить формулу 2.10) и вычислить момент инерции крестовины  (маятника без грузов 5 на стержнях 1).
(маятника без грузов 5 на стержнях 1).
12) Рассматривая цилиндрический груз как стержень, и используя формулу теоремы Штейнера, получить выражение момента инерции четырех грузов через массу  и длину
и длину  груза и расстояние
груза и расстояние  грузов от оси вращения:
грузов от оси вращения:
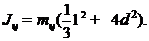
13) Вычислить момент инерции всех четырех цилиндрических грузов  при выбранном расстоянии
при выбранном расстоянии  .
.
14) Вычислить, какую долю от момента инерции маятника  составляют:
составляют:
а) момент инерции крестовины  ;
;
б) момент инерции цилиндров на стержнях  .
.
15) Используя формулы моментов инерции тел и формулу теоремы Штейнера, вычислить:
а) момент инерции  диска (диаметр диска
диска (диаметр диска  = …, масса диска
= …, масса диска 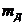 = …);
= …);
б) момент инерции шкивов  ,
, 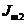 ,
,  =
=  +
+ 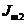 (высота шкива 1 равна
(высота шкива 1 равна  = …; высота шкива 2 равна
= …; высота шкива 2 равна  = …; плотность стали = …);
= …; плотность стали = …);
16) Получить формулу момента инерции стержней относительно оси вращения
 .
.
17). Вычислить момент инерции стержней  (длина стержня
(длина стержня  = …; масса стержня
= …; масса стержня 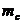 = …; расстояние от оси вращения до центра инерции стержней
= …; расстояние от оси вращения до центра инерции стержней  = …).
= …).
18). Вычислить момент инерции  остальных вращающихся частей маятника (блока 7, подшипников):
остальных вращающихся частей маятника (блока 7, подшипников):
 =
=  –
–  –
–  –
– 
19). Вычислить, какую долю от момента инерции крестовины  составляют:
составляют:
а) момент инерции диска  ;
;
б) момент инерции шкивов  ;
;
в) момент инерции стержней  ;
;
г) момент инерции остальных вращающихся частей маятника  .
.
Студент _______________________________________________
(факультет, курс, группа, фамилия, и.о.)
лабораторную работу выполнил ______________________________
(подпись преподавателя)
задания к лабораторной работе выполнил ___________________
(подпись преподавателя)
Таблица 2.3.1
Таблица 2.3.2
|
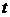 , с
, с
 ,
с
,
с
 с-2
с-2
 Н м
Н м
 Н м
Н м
 кг м2
кг м2
 1/(кг . м2)
1/(кг . м2)