умножить исходное число F на основание системы q

2. выделить целую и дробную части произведения. Целая часть является старшим после запятой разрядом искомого числа. Считать дробную часть произведения исходным числом и повторить пункт 1.

Умножение продолжается до тех пор, пока дробная часть произведения не станет равной 0 или не будет достигнута требуемая точность числа.

ПРИМЕР: Переведем число 0,375 из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную.

в двоичную

в восьмеричную

 

 

в шестнадцатеричную

 

ПРИМЕР: Переведем число 0,6 из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную.

 

 

в двоичную

в восьмеричную:

в шестнадцатеричную:

 

ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ. Переведите десятичную дробь в двоичную, восьмеричную и шестнадцатеричную системы счисления.

Номер варианта	Число	Номер варианта	Число
	0,12		0,51
	0,36		0,17
	0,42		0,83
	0,54		0,28
	0,67		0,49
	0,23		0,62
	0,76		0,31
	0,94		0,92

 

Для чисел, имеющих целую и дробную части, перевод из десятичной системы счисления в другую осуществляется отдельно для целой и дробной части.

 

ПРИМЕР: 53,375₁₀ = 110 101,011₂ = 65,3₈ = 35,6₁₆

ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ №1: Перевести десятичное число, указанное в варианте в двоичную, восьмеричную и шестнадцатеричную системы счисления аналогично данным примерам. Сделать проверку.

 

Номер варианта	Число	Номер варианта	Число	Номер варианта	Число
	101,99		411,54		124,82
	153,61		102,58		152,34
	103,34		213,98		113,33
	112,69		142,23		104,43
	110,83		311,34		508,76
	121,71		111,62		115,97
	143,75		412,56		516,35
	211,28		122,74		123,31
	114,57		212,45		316,76
	125,52		312,84		144,64
	310,35		406,53		215,52
	151,66		411,33		314,73

 

5.3 Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему счисления

Для перевода восьмеричных и шестнадцатеричных чисел в двоичную систему счисления каждая цифра заменяется эквивалентным двоичным числом.

ПРИМЕР: Перевести восьмеричное число 652,1₈ и шестнадцатеричное число 652,1₁₆ в двоичное.

652,1₈ = 110 101 010, 001₂ 652,1₁₆ = 0110 0101 0010, 0001₁₆

 

6 5 2 1 6 5 2 1

 

ПРИМЕР: Перевести шестнадцатеричное число 1А3,F₁₆ в двоичное.

1А3,F₁₆ = 1 1010 0011, 1111₂

 

1 А 3 F

ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ. Перевести восьмеричное и шестнадцатеричное числа в двоичную систему счисления.

Номер варианта	Число	Номер варианта	Число
	1538, 4D116		2438, C4F16
	4138, 13D716		1578, C1216
	3108, 1A816		5178, BF1016
	6208, 9AB16		7108, CE4516
	2618, F56116		3678, FF116
	5468, 8E416		4038, 12A716
	1658, CDE16		6348, AFE16
	7658, 12AA16		2378, 12B16

 

5.4 Перевод числа из двоичной системы счисления в восьмеричную или шестнадцатеричную

 

Для перевода числа из двоичной системы счисления в восьмеричную или шестнадцатеричную его нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной), дополнив, если необходимо нулями, и каждую группу заменить соответствующей восьмеричной или шестнадцатеричной цифрой

 

ПРИМЕР: Перевести двоичное число 10010100010010,101 11₂ в восьмеричное и шестнадцатеричное.

 

10010100010010,101 11₂ = 010 010 100 010 010, 101 110₂ = 2 2 4 2 2, 5 6₈

 

10010100010010,1011 1₂ = 0010 0101 0001 0010, 1011 1000₂ = 2 5 1 2, В8₁₆

 

ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ. Переведите число из двоичной системы счисления в восьмеричную и шестнадцатеричную системы, аналогично приведенным примерам.

 

Номер варианта	Число	Номер варианта	Число
	110010110010,1011		111000101001,001001
	100011010010,011011		100011110010,1001
	110010100110,100101		111000010101,011001
	100111001000,00110		101010100001,00111
	101100001110,100111		110011010101,1011
	110011000100,001001		101010001011,1001
	101000100111,100011		101100011100,001101
	101100001101,001101		101000011111,11001

 

ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ № 2: Перевести восьмеричное и шестнадцатеричное числа в двоичную систему счисления.

Номер варианта	Число	Номер варианта	Число
	22438, C44F16		23538, 4DE116
	13578, C11216		41738, 13D7716
	45178, BF21016		34108, 12A816
	37108, CE64516		62608, 9A7B16
	73678, FF6116		26318, F5A6116
	43038, 124A716		53468, 8E5416
	65348, A6FE16		12658, CD2E16
	24378, 1271B16		76358, 122AA16
	13628, F46516		74318, 1AA316
	42018, 104A716		54318, 1372B16
	63318, A63E16		63428, F16516
	54338, 27CB16		62218, 101A716
	63078, 123A16		33718, A62E16
	54438, A43F16		17238, 12A716
	43518, C03216		16358, F2A616
	65118, B621016		43428, 8E7416
	77408, C46416		32628, CD5E16
	42138, 544F16		36228, 7E7916

ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ № 3: Перевести двоичное число в восьмеричную и шестнадцатеричную системы счисления, разбив их на триады и тетрады соответственно.

 

Номер варианта	Число	Номер варианта	Число
	10110010101,1011011		10000010101,1001001
	11100101010,1010011		11111001011,00011
	10010001100,100101		10010001010,01011101
	10110100010,1101101		10011111100,101011
	11010100100,001101		11011100001,110011
	10001010100,00111		10011111000,0010101
	10111010100,01001		11000010110,1010111
	11100101001,110101		10000111111,101101
	10001111011,100101		10101010001,1001101
	10111010101,1001101		10111000111,011001
	11000000011,100111		10000001111,100101
	10000011101,0010101		11111000001,0011001
	10001111100,11011		10000111110,1001001
	10101010000,11101		10011110101,011101
	10011110101,101111		11110011111,0110111
	10101000001,100001		10011111001,01101111
	11001111001,01101		10110000011,1010011
	10110000111,101001		10011111100,01000111

 

6 Арифметические операции в позиционных системах счисления

 

Во всех позиционных системах счисления арифметические операции выполняются так же, как и в десятичной системе – сложение, вычитание и умножение – столбиком, деление – углом. Для каждой системы счисления существуют свои таблицы сложения и умножения.

6.1 Сложение

Таблицы сложения составляются с помощью Правила Счета.

Сложение в двоичной системе

+	0 1
	0 1 1 10

Сложение в восьмеричной системе

+	0 1 2 3 4 5 6 7
	0 1 2 3 4 5 6 7 1 2 3 4 5 6 7 10 2 3 4 5 6 7 10 11 3 4 5 6 7 10 11 12 4 5 6 7 10 11 12 13 5 6 7 10 11 12 13 14 6 7 10 11 12 13 14 15 7 10 11 12 13 14 15 16

Сложение в шестнадцатеричной системе

+

A

B

C

D

E

F

A

B

C

D

E

F

A

B

C

D

E

F

A

B

C

D

E

F

A

B

C

D

E

F

A

B

C

D

E

F

A

B

C

D

E

F

A

B

C

D

E

F

A

B

C

D

E

F

A

B

C

D

E

F

A

B

C

D

E

F

A

A

B

C

D

E

F

B

B

C

D

E

F

1A

C

C

D

E

F

1A

1B

D

D

E

F

1A

1B

1C

E

E

F

1A

1B

1C

1D

F

F

1A

1B

1C

1D

1E

 

При сложении цифры суммируются по разрядам, и, если при этом возникает переполнение, то разряд переносится влево.

 

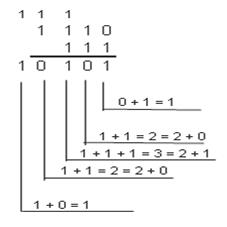
ПРИМЕР1: Сложить числа 14 и 7 в различных позиционных системах счисления.

Десятичная: 14₁₀ + 7₁₀ Двоичная: 1 110₂ + 111₂ Восьмеричная: 16₈ + 7₈

 

 

Шестнадцатеричная: Е₁₆ + 7₁₆

 

Ответ: 14 + 7 = 21₁₀ = 10 101₂ = 25₈ = 15₁₆

 

Проверка. Преобразуем полученные двоичные, восьмеричные и шестнадцатеричные суммы в десятичные:

10 101₂ = 1 x 2⁴ + 0 x 2³ + 1 x 2² + 0 x 2¹ + 1 x 2⁰ = 16 + 0 + 4 + 0 + 1 = 21₁₀

25₈ = 2 x 8¹ + 5 x 8⁰ = 16 + 5 = 21₁₀

15₁₆ = 1 x 16¹ + 5 x 16⁰ = 16 + 5 = 21₁₀

 

ПРИМЕР 2: Сложить числа 15, 6 и 4 в различных позиционных системах счисления.

Десятичная:15₁₀ + 6₁₀ + 4₁₀ Двоичная: 1 111₂ + 110₂ + 100₂

 

 

Восьмеричная: 17₈ + 6₈ + 4₈ Шестнадцатеричная: F₁₆ + 6₁₆ + 4₁₆

 

Ответ: 15₁₀ + 6₁₀ + 4₁₀ = 25₁₀ = 11 001₂ = 31₈ = 19₁₆

Проверка. Преобразуем полученные двоичные, восьмеричные и шестнадцатеричные суммы в десятичные:

11 001₂ = 1 x 2⁴ + 1 x 2³ + 0 x 2² + 0 x 2¹ + 1 x 2⁰ = 16 + 8 + 0 + 0 + 1 = 25₁₀

31₈ = 3 x 8¹ + 1 x 8⁰ = 24 + 1 = 25₁₀

19₁₆ = 1 x 16¹ + 9 x 16⁰ = 16 + 9 =25₁₀

ПРИМЕР3: Сложить числа 41,5 и 31,75 в различных позиционных системах счисления.

Десятичная: 41,5₁₀ + 31,75₁₀ Двоичная: 101 001,1 + 11 111,11

 

 

Восьмеричная: 51,4₈ + 37,6₈ Шестнадцатеричная: 29,8₁₆ + 1F,C₁₆

 

 

Ответ: 41,5₁₀ + 31,75₁₀ = 73,25₁₀ = 1 001 001,01₂ = 111,2₈ = 49,4₁₆

Проверка. Преобразуем полученные двоичные, восьмеричные и шестнадцатеричные суммы в десятичные:

1 001 001,01₂ = 1x2⁶ + 0x2⁵ + 0x2⁴ + 1x2³ + 0x2² + 0x2¹ + 1x2⁰ + 0x2^-1 + 1x 2^-2 =

= 64 + 0 + 0 + 8 + 0 + 0 + 1 + 0 + 1/4 =

= 73,25₁₀

111,2₈ = 1 x 8² + 1 x 8¹ + 1 x 8⁰ + 2 x 8^-1 = 64 + 8 + 1 + 2/8 = 73,25₁₀

49,4₁₆ = 4 x 16¹ + 9 x 16⁰ + 4 x 16^-1 = 64 + 9 + 4/16 = 73,25₁₀

 

ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ. Сложить числа в различных позиционных системах счисления, аналогично примеру 1.Сделать проверку.

 

Номер варианта	Числа	Номер варианта	Числа
	18 и 56		49 и 39
	34 и 12		27 и 58
	63 и 34		76 и 26
	48 и 14		14 и 79
	25 и 23		82 и 17
	72 и 41		57 и 34
	52 и 23		36 и 47
	85 и 23		68 и 16

 

6.2 Вычитание

Рассмотрим приемы вычитания в различных позиционных системах счисления на примерах.

ПРИМЕР1: Вычтем единицу из чисел 10₁₀, 10₂, 10₈ и 10₁₆.

Десятичная: 10₁₀ – 1₁₀ Двоичная: 10₂ – 1₂ Восьмеричная: 10₈–1₈

 

Шестнадцатеричная:

 

 

 

ПРИМЕР2: Вычтем единицу из чисел 100₂, 100₈ и 100₁₆.

Двоичная: 100₂ – 1₂ Восьмеричная: 100₈ – 1₈Шестнадцатеричная: 100₁₆ – 1₁₆

 

 

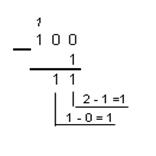
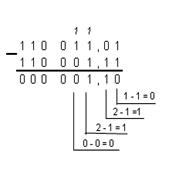
ПРИМЕР3: Вычтем число 49,75 из числа 51,25 в различных позиционных системах счисления.

Десятичная: 51,25₁₀ -49,75₁₀ Двоичная:110011,01₂ –110001,11₂

 

Восьмеричная: 63,2₈– 61,6₈ Шестнадцатеричная: 33,4₁₆ – 31,С₁₆

 

Ответ: 51,25₁₀ - 49,75₁₀ = 1,5₁₀ =1,1₂ = 1,4₈ = 1,8₁₆

Проверка. Преобразуем полученные двоичные, восьмеричные и шестнадцатеричные разности в десятичные:

1,1₂ = 1 x 2⁰ + 1 x 2^-1 = 1 + Ѕ = 1,5₁₀

1,4₈ = 1 x 8⁰ + 4 x 8^-1 = 1 + 4/8 = 1 + Ѕ = 1,5₁₀

1,8₁₆ = 1 x 16⁰ + 8 x 16^-1 = 1 + 8/16 = 1 + Ѕ = 1,5₁₀

 

ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ. Вычесть числа в различных позиционных системах счисления. Сделать проверку.

Номер варианта	Числа	Номер варианта	Числа
	49 и 39		98 и 56
	67 и 58		31 и 19
	98 и 56		83 и 39
	34 и 12		48 и 14
	63 и 35		65 и 28
	41 и 14		83 и 49
	85 и 23		52 и 23
	72 и 48		45 и 29

 

ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ № 1: Найти сумму и разность чисел, аналогично предыдущим примерам. Сделать проверку.

 

Номер варианта	Число	Номер варианта	Число
	90,5 и 16,28125		76,25 и 38,375
	56,5625 и 16,5		65,25 и 29,28125
	75,625 и 36,5		83,75 и 42,125
	49,25 и 28,53125		54,3125 и 19,375
	84,375 и 23,5		57,125 и 23,25
	59,125 и 33,0625		71,375 и 39,0625
	44,28125 и 28,375		96,53125 и 53,125
	68,0625 и 42,375		32,125 и 29,0625
	81,28125 и 20,25		75,28125 и 34,125
	46,75 и 28,3125		86,125 и 43,28125
	96,25 и 12,5		56,25 и 17,375
	52,0625 и 11,125		69,28125 и 23,5
	61,125 и 49,75		72,25 и 59,0625
	62,5625 и 38,375		87,0625 и 49,375
	77,5625 и 35,5		41,375 и 19,53125
	67,25 и 36,53125		74,28125 и 32,75
	54,625 и 23,0625		82,25 и 44,125
	64,125 и 27,375		98,0625 и 52,5

 

 

6.3 Прямой, обратный и дополнительный двоичные коды

 

В компьютерной арифметике, которая базируется на двоичной системе счисления, операция «вычитания» заменяется операцией «сложения».

Рассмотрим, как это происходит.

Для хранения целых чисел в памяти ЭВМ выделяется фиксированное число двоичных разрядов – бит. Рассмотрим 8 – и битовое представление числа. Каждый бит нумеруется «слева – направо» от 0 до 7.

вес разряда   нумерация бит в байте

 

26

25

24

23

22

21

20

7 6 5 4 3 2 1 0

 

Старший бит – седьмой – используется для знака числа: 0 – это положительное число, 1 – отрицательное.

Если в 6-и разрядах байта поместить абсолютное значение числа, а в 7-ом бите установить его знак (0 или 1), то полученное представление числа называется прямым двоичным кодом.

Если в прямом коде число представлено как отрицательное (7-ой бит равен 1), то в числе инвертируются [2] все разряды, кроме знакового. Такое представление числа называется обратный двоичный код.

После прибавления к обратному коду 1 получается дополнительный двоичный код.

Использование дополнительного двоичного кода позволяет создавать схемы, выполняющие вычитание, умножение и деление посредством операции сложения.

Рассмотрим на примерах операцию вычитания для 8-и битовых чисел.

ПРИМЕР1: Вычесть число 3 из 5 (101₂ – 011₂).

· Запишем абсолютное значение числа -3 в байте

 

· В знаковый – седьмой – бит запишем признак отрицательности числа 1 и получим прямой двоичный код числа -3.

 

· Инвертируем все разряды в числе, кроме знакового

Получим обратный двоичный код числа -3.

 

· Прибавим к обратному коду единицу

Получим дополнительный двоичный код числа -3.

· Сложим число 5 и дополнительный двоичный код числа -3

Получили число 010₂ = 2₁₀.

Ответ: 101₂ – 011₂ = 010₂

Проверка: Сделаем проверку, преобразуя двоичные числа к десятичному виду:

5₁₀ – 3₁₀ = 2₁₀

ПРИМЕР2: Вычесть число 49 из 63

· Прямой двоичный код числа -49

 

· Инверсный код числа -49

 

· Дополнительный код числа -49

 

· Сложим число 63 и дополнительный код числа -49

Получили число 1110₂ = 14₁₀

Ответ: 11 1111₂ – 11 0001₂ = 1110₂

Проверка: 63₁₀ – 49₁₀ = 14₁₀

ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ. Используя схемы примера 1 или 2, сделайте вычитание целых чисел, используя дополнительный двоичный код.

 

Номер варианта	Число	Номер варианта	Число
	81 и 17		64 и 32
	42 и 18		51 и 28
	42 и 36		92 и 48
	61 и 28		67 и 29
	74 и 28		82 и 29
	62 и 39		53 и 29
	43 и 28		83 и 38
	78 и 49		68 и 29

 

ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ № 2. Используя схемы примера 1 или 2, сделайте вычитание целых чисел, используя дополнительный двоичный код.

Номер варианта	Число	Номер варианта	Число
	74 и 32		91 и 16
	61 и 28		52 и 19
	82 и 48		72 и 36
	57 и 19		41 и 28
	52 и 29		84 и 29
	73 и 39		52 и 33
	93 и 58		41 и 28
	38 и 29		68 и 49
	75 и 36		81 и 27
	81 и 43		43 и 28
	56 и 19		91 и 12
	61 и 23		52 и 19
	72 и 53		61 и 48
	81 и 43		63 и 38
	41 и 29		72 и 35
	74 и 38		63 и 36
	81 и 49		54 и 29
	91 и 52		62 и 27

6.4 Умножение

При умножении многозначных чисел в различных позиционных системах счисления используется обычный алгоритм перемножения чисел в столбик. Результаты умножения и сложения однозначных чисел берутся из таблиц умножения и сложения соответствующей системы счисления.

Умножение в двоичной системе

*

 

Умножение в восьмеричной системе

 

*

 

Умножение в шестнадцатеричной системе

*

A

B

C

D

E

F

A

B

C

D

E

F

A

C

E

1A

1C

1E

C

F

1B

1E

2A

2D

C

1C

2C

3C

A

F

1E

2D

3C

4B

C

1E

2A

3C

4E

5A

E

1C

2A

3F

4D

5B

1B

2D

3F

5A

6C

7E

A

A

1F

3C

5A

6E

8C

B

B

2C

4D

6E

8F

9A

A5

C

C

3C

6C

9C

A8

B4

D

D

1A

4E

5B

8F

9C

A9

B6

C3

E

E

1C

2A

7E

8C

9A

A8

B6

C4

D2

F

F

1E

2D

3C

4B

5A

A5

B4

C3

D2

E1

 

 

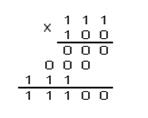
ПРИМЕР1: Перемножим числа 7 и 4 в различных системах счисления.

 

Десятичная: 7₁₀ x 4₁₀ Двоичная: 111₂ x 100₂ Восьмеричная: 7₈ x 4₈

 

 

Шестнадцатеричная: 7₁₆ x 4₁₆

 

 

Ответ: 7 x 4 = 28₁₀ = 11 100₂ = 34₈ = 1C₁₆

Проверка: Преобразуем полученные произведения к десятичному виду:

11 100₂ = 1 x 2⁴ + 1 x 2³ + 1 x 2² + 0 x 2¹ +0 x 2⁰ = 16 + 8 + 4 + 0 + 0 = 28₁₀

34₈ = 3 x 8¹ + 4 x 8⁰ = 24 + 4 = 28₁₀

1C₁₆ = 1 x 16¹ + C x 16⁰ = 16 + 12 = 28₁₀

ПРИМЕР2: Перемножим числа 123 и 15 в различных системах счисления.

Десятичная: 123₁₀x15₁₀ Двоичная: 1111011₂x 1111₂ Восьмеричная: 173₈ x 17₈

 

 

 

Шестнадцатеричная: 7₁₆ x 4₁₆

 

 

Ответ: 123 x 15 = 1845₁₀ = 11 100 110 101₂ = 3465₈ = 735₁₆

Проверка: Преобразуем полученные произведения к десятичному виду:

11100110101₂=1x2¹⁰+1x2⁹+1x2⁸+0x2⁷+0x2⁶+1x2⁵+1x2⁴+0x2 ³+1x2²+0x2¹+1x2⁰

=1024 +512 + 256 + 0 + 0 + 32 + 16 + 0 + 4 + 0 + 1

= 1845₁₀

3465₈ = 3 x 8³ + 4 x 8² + 6 x 8¹ + 5 x 8⁰ = 1536 + 256 + 48 + 5 = 1845₁₀

735₁₆ = 7 x 16² + 3 x 16¹ + 5 x 16⁰ = 1792 + 48 + 5 = 1845₁₀

ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ. Сделайте умножение целых чисел в различных системах счисления.

Номер варианта	Число	Номер варианта	Число
	47 и 23		56 и 26
	26 и 82		68 и 43
	82 и 28		56 и 52
	67 и 27		67 и 34
	52 и 39		28 и 54
	83 и 29		51 и 83
	39 и 82		49 и 79
	87 и 49		34 и 78

6.5 Деление

Деление в любой позиционной системе счисления производится по тем же правилам, как и в десятичной системе. В двоичной системе очередная цифра частного может быть или нулем или единицей.

ПРИМЕР1: Разделим число 42 на число 6 в различных системах счисления.

Десятичная: 42₁₀: 6₁₀ Двоичная: 101 010₂: 110₂ Восьмеричная: 52₈: 6₈

 

Шестнадцатеричная: 2А₁₆: 6₁₆

 

 

Ответ: 42: 6 = 7₁₀ = 111₂ = 7₈ = 7₁₆

Проверка: Преобразуем полученные частные к десятичному виду:

111₂ = 1 x 2² + 1 x 2¹ + 1 x 2⁰ = 4 + 2 + 1 = 7₁₀

7₈ = 7 x 8⁰ = 7₁₀

7₁₆ = 7 x 16⁰ = 7₁₀

ПРИМЕР2: Разделим число 246 на число 41 в различных системах счисления.

Десятичная:246₁₀:41₁₀ Двоичная:11110110₂: 101001₂ Восьмеричная: 66₈:51₈

 

 

Шестнадцатеричная: F6₁₆: 29₁₆

 

 

Ответ: 246: 41 = 6₁₀ = 110₂ = 6₈ = 6₁₆

Проверка: Преобразуем полученные частные к десятичному виду:

110₂ = 1 x 2² + 1 x 2¹ + 0 x 2⁰ = 4 + 2 + 0 = 6₁₀

6₈ = 6 x 8⁰ = 6₁₀

6₁₆ = 6 x 16⁰ = 6₁₀

 

ПРИМЕР3: Разделим число 54 на число 12 в различных системах счисления.

Десятичная: 54₁₀: 12₁₀ Двоичная: 110 110₂: 1 100₂ Восьмеричная: 66₈: 14₈

 

Шестнадцатеричная: 36₁₆: C₁₆

 

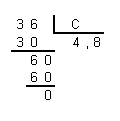
Ответ: 54: 12 = 4,5₁₀ = 100,1₂ = 4,4₈ = 4,8₁₆

Проверка: Преобразуем полученные частные к десятичному виду:

100,1₂ = 1 x 2² + 0 x 2¹ + 0 x 2⁰ + 1 x 2^-1 = 4 + 0 + 0 + Ѕ = 4,5₁₀

4,4₈ = 4 x 8⁰ + 4 x 8^-1 = 4 + 1/8 = 4,5₁₀

4,8₁₆ = 4 x 16⁰ + 8 x 16^-1 = 4 + 8/16 = 4,5₁₀

ЗА