ПРАКТИЧЕСКАЯ РАБОТА № 3.
Составить развозочный маршрут по критерию минимального пробега автомобиля. Автомобиль отправляется из пункта А и после объезда пунктов Б, В, Г, Д, Е, Ж возвращается в пункт А.

Рис. 3.1 – Технологические требования к созданию информационного обеспечения по формированию развозочного (сборочного) маршрута.
Таблица 3.1 – Исходные данные для выполнения работы №3
| Вариант | Координаты пунктов | ||||||
| А | Б | В | Г | Д | Е | Ж | |
| 1; 1 | 3; 5 | 3; 3 | 5; 2 | 9; 7 | 7; 3 | 5; 5 | |
| 4; 1 | 3; 5 | 6; 3 | 2; 2 | 1; 7 | 7; 4 | 3; 5 | |
| 3; 5 | 1; 2 | 5; 3 | 3; 9 | 3; 3 | 7; 3 | 8; 2 | |
| 2; 2 | 1; 7 | 7; 4 | 3; 5 | 3; 9 | 1; 2 | 5; 3 | |
| 2; 4 | 1; 1 | 3; 5 | 5; 3 | 3; 9 | 1; 3 | 5; 4 | |
| 1; 7 | 5; 3 | 3; 5 | 3; 9 | 1; 2 | 5; 3 | 3; 3 | |
| 3; 3 | 5; 2 | 9; 7 | 4; 1 | 6; 3 | 1; 1 | 3; 5 | |
| 6; 3 | 2; 2 | 1; 7 | 7; 4 | 1; 1 | 4; 1 | 3; 5 | |
| 5; 3 | 3; 9 | 3; 3 | 7; 4 | 1; 1 | 3; 5 | 1; 2 | |
| 1; 4 | 7; 1 | 1; 5 | 7; 4 | 3; 5 | 2; 2 | 1; 7 | |
| 1; 8 | 3; 5 | 5; 3 | 7; 3 | 8; 2 | 2; 4 | 1; 1 | |
| 1; 3 | 3; 5 | 6; 9 | 3; 2 | 5; 9 | 5; 7 | 5; 3 | |
| 9; 7 | 7; 3 | 5; 5 | 1; 1 | 3; 5 | 3; 3 | 5; 2 | |
| 1; 7 | 7; 4 | 3; 5 | 4; 1 | 3; 5 | 6; 3 | 2; 2 | |
| 3; 3 | 7; 3 | 8; 2 | 3; 5 | 1; 2 | 5; 3 | 3; 9 | |
| 3; 9 | 1; 2 | 5; 3 | 2; 2 | 1; 7 | 7; 4 | 3; 5 | |
| 3; 9 | 1; 3 | 5; 4 | 2; 4 | 1; 1 | 3; 5 | 5; 3 | |
| 1; 2 | 5; 3 | 3; 3 | 1; 7 | 5; 3 | 3; 5 | 3; 9 | |
| 6; 3 | 1; 1 | 3; 5 | 3; 3 | 5; 2 | 9; 7 | 4; 1 | |
| 3; 7 | 7; 8 | 4; 1 | 6; 3 | 2; 2 | 1; 7 | 7; 4 |
Методические указания к заданию № 3
Данная задача носит название «задача «коммивояжера».
Она формулируется следующим образом: имеются  пунктов
пунктов 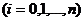 с заданными расстояниями
с заданными расстояниями  между i-м и k-м пунктами. Составить оптимальный маршрут из условия минимизации суммарного пробега для машины, выходящей из «нулевого» пункта, которая должна побывать в каждом пункте по одному и только одному разу и вернуться в «нулевой» пункт.
между i-м и k-м пунктами. Составить оптимальный маршрут из условия минимизации суммарного пробега для машины, выходящей из «нулевого» пункта, которая должна побывать в каждом пункте по одному и только одному разу и вернуться в «нулевой» пункт.
Решение. Введем n2 альтернативных переменных xik, принимающих значение 0, если переезд из i-го пункта в k-й не входит в маршрут, и 1 в противоположном случае. Условия прибытия машины в каждый пункт и выезда из каждого пункта только по одному разу могут быть выражены равенствами
 (3.1)
(3.1)
Однако необходимо обеспечить «непрерывность» маршрута, т.е. чтобы набор «звеньев» (i,k), для которых xik =1 (т.е. звеньев, входящих в маршрут) образовал единую цепочку (например, при n=7 цепочка (1.1)-(3.3)-(3.5)-(5.5)-(5.2)-(7.3)-(9.7), а не состоял бы из отдельных не связанных цепочек (например, (0,1)-(1,5)-(5,0) и (2,7)-(7,6)-(6,4)-(4,3)-(3,2)]. Это условие можно обеспечить введением дополнительных n переменных 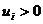
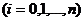 и дополнительных n2 ограничений
и дополнительных n2 ограничений
(1.1)-(3.3)-(3.5)-(5.5)-(5.2)-(7.3)-(9.7)
7*1+33-26 меньше 7-1
14 меньше 6 (3.2)
Действительно, пусть маршрут включает несколько цепочек. Тогда существует цепочка, начинающаяся и заканчивающаяся в «нулевом» пункте, но охватывающая n1 звеньев, где n1<n. Просуммировав неравенства вдоль такой цепочки (т.е. при xik=1), получим бессмысленное неравенство n1∙n ≤ n1∙(n-1) (все ui и uk при суммировании взаимно уничтожаются).
Суммарная длина пробега машины z, которую необходимо минимизировать, запишется в виде
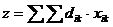
Z=58*1=58 (3.3)
В результате приходим к следующей модели частично целочисленной задачи: минимизировать z при условиях (3.1), (3.2), условиях неотрицательности 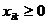
 и
и 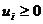
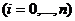 и целочисленности всех переменных xik.
и целочисленности всех переменных xik.
ПРАКТИЧЕСКАЯ РАБОТА № 3.
Составить развозочный маршрут по критерию минимального пробега автомобиля. Автомобиль отправляется из пункта А и после объезда пунктов Б, В, Г, Д, Е, Ж возвращается в пункт А.

Рис. 3.1 – Технологические требования к созданию информационного обеспечения по формированию развозочного (сборочного) маршрута.
Таблица 3.1 – Исходные данные для выполнения работы №3
| Вариант | Координаты пунктов | ||||||
| А | Б | В | Г | Д | Е | Ж | |
| 1; 1 | 3; 5 | 3; 3 | 5; 2 | 9; 7 | 7; 3 | 5; 5 | |
| 4; 1 | 3; 5 | 6; 3 | 2; 2 | 1; 7 | 7; 4 | 3; 5 | |
| 3; 5 | 1; 2 | 5; 3 | 3; 9 | 3; 3 | 7; 3 | 8; 2 | |
| 2; 2 | 1; 7 | 7; 4 | 3; 5 | 3; 9 | 1; 2 | 5; 3 | |
| 2; 4 | 1; 1 | 3; 5 | 5; 3 | 3; 9 | 1; 3 | 5; 4 | |
| 1; 7 | 5; 3 | 3; 5 | 3; 9 | 1; 2 | 5; 3 | 3; 3 | |
| 3; 3 | 5; 2 | 9; 7 | 4; 1 | 6; 3 | 1; 1 | 3; 5 | |
| 6; 3 | 2; 2 | 1; 7 | 7; 4 | 1; 1 | 4; 1 | 3; 5 | |
| 5; 3 | 3; 9 | 3; 3 | 7; 4 | 1; 1 | 3; 5 | 1; 2 | |
| 1; 4 | 7; 1 | 1; 5 | 7; 4 | 3; 5 | 2; 2 | 1; 7 | |
| 1; 8 | 3; 5 | 5; 3 | 7; 3 | 8; 2 | 2; 4 | 1; 1 | |
| 1; 3 | 3; 5 | 6; 9 | 3; 2 | 5; 9 | 5; 7 | 5; 3 | |
| 9; 7 | 7; 3 | 5; 5 | 1; 1 | 3; 5 | 3; 3 | 5; 2 | |
| 1; 7 | 7; 4 | 3; 5 | 4; 1 | 3; 5 | 6; 3 | 2; 2 | |
| 3; 3 | 7; 3 | 8; 2 | 3; 5 | 1; 2 | 5; 3 | 3; 9 | |
| 3; 9 | 1; 2 | 5; 3 | 2; 2 | 1; 7 | 7; 4 | 3; 5 | |
| 3; 9 | 1; 3 | 5; 4 | 2; 4 | 1; 1 | 3; 5 | 5; 3 | |
| 1; 2 | 5; 3 | 3; 3 | 1; 7 | 5; 3 | 3; 5 | 3; 9 | |
| 6; 3 | 1; 1 | 3; 5 | 3; 3 | 5; 2 | 9; 7 | 4; 1 | |
| 3; 7 | 7; 8 | 4; 1 | 6; 3 | 2; 2 | 1; 7 | 7; 4 |
Методические указания к заданию № 3
Данная задача носит название «задача «коммивояжера».
Она формулируется следующим образом: имеются  пунктов
пунктов 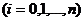 с заданными расстояниями
с заданными расстояниями  между i-м и k-м пунктами. Составить оптимальный маршрут из условия минимизации суммарного пробега для машины, выходящей из «нулевого» пункта, которая должна побывать в каждом пункте по одному и только одному разу и вернуться в «нулевой» пункт.
между i-м и k-м пунктами. Составить оптимальный маршрут из условия минимизации суммарного пробега для машины, выходящей из «нулевого» пункта, которая должна побывать в каждом пункте по одному и только одному разу и вернуться в «нулевой» пункт.
Решение. Введем n2 альтернативных переменных xik, принимающих значение 0, если переезд из i-го пункта в k-й не входит в маршрут, и 1 в противоположном случае. Условия прибытия машины в каждый пункт и выезда из каждого пункта только по одному разу могут быть выражены равенствами
 (3.1)
(3.1)
Однако необходимо обеспечить «непрерывность» маршрута, т.е. чтобы набор «звеньев» (i,k), для которых xik =1 (т.е. звеньев, входящих в маршрут) образовал единую цепочку (например, при n=7 цепочка (1.1)-(3.3)-(3.5)-(5.5)-(5.2)-(7.3)-(9.7), а не состоял бы из отдельных не связанных цепочек (например, (0,1)-(1,5)-(5,0) и (2,7)-(7,6)-(6,4)-(4,3)-(3,2)]. Это условие можно обеспечить введением дополнительных n переменных 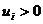
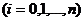 и дополнительных n2 ограничений
и дополнительных n2 ограничений
(1.7)-(7.4)-(4.1)-(3.5)-(3.5)-(6.3)-(2.2)
7*1+27-26 меньше 7-1
8 меньше 6 (3.2)
Действительно, пусть маршрут включает несколько цепочек. Тогда существует цепочка, начинающаяся и заканчивающаяся в «нулевом» пункте, но охватывающая n1 звеньев, где n1<n. Просуммировав неравенства вдоль такой цепочки (т.е. при xik=1), получим бессмысленное неравенство n1∙n ≤ n1∙(n-1) (все ui и uk при суммировании взаимно уничтожаются).
Суммарная длина пробега машины z, которую необходимо минимизировать, запишется в виде
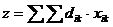
Z=52*1=52 (3.3)
В результате приходим к следующей модели частично целочисленной задачи: минимизировать z при условиях (3.1), (3.2), условиях неотрицательности 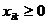
 и
и 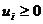
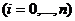 и целочисленности всех переменных xik.
и целочисленности всех переменных xik.