Шифрование по таблице
Для зашифрования слова из 5 букв на русском языке его: 1) преобразовали с помощью таблицы (рис. 1) в цепочку чисел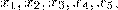 
2) выбрали (секретное) натуральное число 
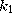и дописали сумму 
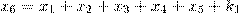к цепочке справа, 3) в расширенной цепочке 
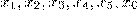числа 
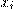заменили числами 
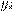по формулам: 
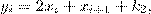, если 
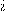нечетное; 
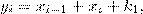, если 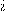четное, где 
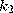еще одно (секретное) натуральное число и, наконец, 4) каждое 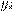заменили его остатком от деления на 31. В результате получили вот что: 28, 12, 5, 0, 11, 14. Найдите исходное сообщение.
Решение
Выпишем систему уравнений:
+.
где
.
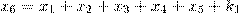Сложив каждое четное уравнение системы, получим:
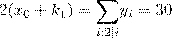
и
.
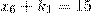Из двух последних уравнений системы, находим:
.
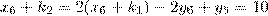Возьмем разность двух полученных уравнений, находим: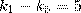 
Теперь нетрудно установить, что:
В результате имеем:
| У | И | А |
А если отнять из второго уравнения системы четвертое, можно установить, что:
,
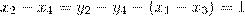то есть четные буквы находятся путем перебора вариантов для второй буквы.
Ответ: УЛИКА.
Коммуникатор
Разблокировка коммуникатора осуществляется вводом 4-значного числового кода на сенсорном экране. На клавиатуре первоначальная расстановка цифр после ввода кода меняется в зависимости от случайного простого числа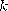 
от 7 до 2017, и на месте цифры 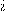отображается значение 
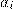равное последней цифре числа 
. Пользователь вводит цифры из левой колонки левой рукой, а остальные правой. Восстановите код блокировки, если известно, что при наборе кода пользователь вводил цифры следующим образом:
при 
: левой, правой, правой, правой;
при 
: правой, правой, левой, левой;
при 
: левой, левой, правой, правой;
при 
: правой, правой, левой, правой.
| 
| 
|
| 
| 
|
| 
| 
|
|
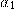
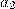
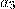
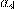
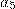
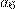
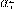
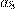
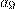
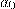
Решение
Из признаков делимости на 2 и на 5 следует, что простое число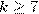 
не может оканчиваться на четную цифру и на цифру 5. Следовательно, такое простое число может оканчиваться лишь на цифры 1, 3, 7, 9. Обозначим, через 
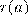– последнюю цифру числа 
, тогда ясно, что выполняется свойство: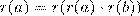 
. Поэтому раскладка клавиатуры определяются лишь указанными последними цифрами – 1, 3, 7, 9. Таким образом, возможны 4 варианта раскладки клавиатуры:
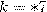
Теперь несложно понять, что в условиях задачи следует рассматривать все раскладки:
Первая цифра кода при находится в первом столбце, значит это 1, 4 или 7, при эта цифра лежит также в первом столбце – следовательно, она равна 7. Вторая цифра кода при лежит в первом столбце, значит это 7, 8 или 9. Во всех остальных раскладках она лежит в других столбцах (2 -ом или 3-ем). Как видно, таким свойством обладает только цифра 8. Аналогичным образом рассуждая, придем к тому, что единственной комбинацией, удовлетворяющей условиям задачи, будет 7832
Построение шифратора
Для записи текста используются только заглавные буквы, пробелы, точки и запятые – всего различных 36 символов. При зашифровании каждый символ заменили числом от 0 до 35 в соответствии с порядком в «расширенном» алфавите. Затем полученную последовательность чисел разбили на пары, а каждую пару заменили по правилу: пару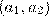 
заменили на пару 
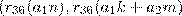, где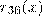 
– остаток от деления числа x на 36, а n, k и m – заранее выбранные целые числа от 0 до 35. Найдите все наборы чисел n, k и m, при которых разные пары переходят в разные (это необходимо для возможности расшифрования текста). Сформулируйте правило расшифрования для случая n = k = m = 17. Решение обоснуйте.
Решение
Условие задачи равносильно тому, что при «правильно» выбранных n, k и m система состоящая из уравнений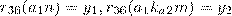 
┤ имеет единственное решение 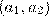при любой паре 
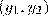. В этом случае разные пары 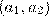будут переходить в разные 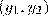, иначе получим противоречие с единственностью решения такой системы при некоторой паре 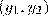. Обратно, если разные пары 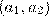переходят в разные пары 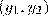, то при любой паре 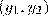такая система либо имеет единственное решение, либо не имеет решений. Однако в то же время количество различных пар 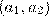равно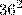 
, а значит количество соответствующих им различных пар 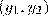по крайней мере 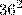, но ясно, что их число не превосходит 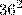, а стало быть оно в точности равно 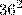. Отсюда следует, что для любой пары 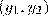рассматриваемая система имеет решение и при том только одно. Можно показать, что уравнение 
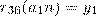имеет единственное решение 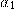при любом 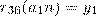тогда и только тогда, когда n и 36 взаимнопросты. Следовательно, если n и 36 взаимнопросты, то из данного уравнения значение 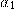находится однозначно и тогда второе уравнение системы примет вид: 
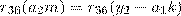. Аналогично, оно имеет единственное решение относительно 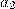при любом 
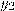тогда и только тогда, когда m и 36 взаимнопросты, при этом значение параметра k на это свойство никак не влияет. Таким образом, однозначное расшифрование возможно при выборе взаимнопростых с 36 числах n, m и произвольном k. Пусть теперь n=k=m=17. Тогда для нахождения 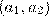нужно решить систему уравнений: 
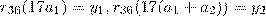. Легко видеть, что 
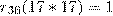. Отсюда легко проверить, что 
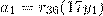и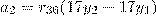 
.
Общий секрет Миллы и Стеллы
Милла и Стелла разговаривают по телефону и хотят выбрать секретное число
так, чтобы оно осталось неизвестным постороннему, возможно подслушивающему
разговор. Для этого Милла подбирает натуральное число a ≤ 256 такое, что числа
r257(ai) – различны при всех 1 ≤ i ≤ 256 и r257(a256) = 1, где r257(t) – остаток от де-
ления числа t на 257. Затем Милла загадывает натуральное число x ≤ 256, а Стелла–
натуральное число y ≤ 256. После этого Милла сообщает числа a и r257(ax) Стелле, а
Стелла ей – число r257(ay). Теперь они обе вычисляют их секретное число r257(axy).
Найдите его, если известно, что r257(ax) = 9, r257(ay) = 256.
Решение
Обозначим через r257(x) – остаток от деления на 257 числа x.
Так как r257(ax) = 9 = r257(32) =r257(((r257(at))2)= r257(a2t),
де 1 ≤ t ≤ 256, r257(at) = 3. Тогда x = 2t или x = 2t - 256 = 2t’.
Тогда r257(axy) = r257((256)x) = r257(r257((-1)x)) = r257((-1)2t) = 1.
Переписка Кати и Юры
Для шифрования передаваемых сообщений Катя и Юра используют следующий способ. Юра заранее выбрал набор коэффициентов (2, 5, 8, 16), натуральное число u и сообщил их Кате. Для шифрования сообщения (x1,x2,x3,x4), состоящего из нулей и единиц, Катя вычисляет сумму S = 2x1 + +5x2+ 8x3 + 16x4, а затем находит остаток S′ от деления произведения Su на 32 и отсылает S′ Юре. Помогите Юре расшифровать сообщение S′ = 11, то есть найти соответствующую ему строку (x+++1,x2,x3,x4), если известно, что остаток от деления числа 7u на 32 равен 1.
Решение
Обозначим через rM(b) - остаток от деления числа b на M. Запишем чему равно число S′ согласно определению деления натуральных чисел с остатком:
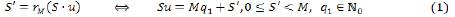
Поскольку известно, что остаток от деления 7u на M равен 1, то запишем: 
Домножим обе части (1) на 7 и подставим в полученное равенство вместо 7u равенство (2). Имеем: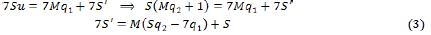 
Заметим далее, что натуральное число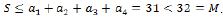 
Поэтому полученное равенство (3) есть не что иное, как деление 7S′ с остатком на M и, кроме того, rM(7S′) = S. Таким образом, найдя остаток от деления 7S′ на M, получим исходное число S.
В нашем случае,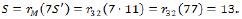 
Теперь, зная S, осталось найти (x1,x2,x3,x4). Но это делается легко. Действительно, равенство x4 = 0 очевидно, поскольку S < 16. Дальше можно перебрать все возможные восемь вариантов, либо сразу заметить, что x2 = x3 = 1, x1 = 0(что просто угадывается), либо последовательно вычитать из S числа a3,a2, a1 пока не получим нуль, полагая при этом, что соответствующий xi = 1.
Восстановление бита
Известно, что три числа a1, a2, a3 были получены следующим образом. Сначала выбрали натуральное число A и нашли числа A1= [A]16, A2= [A/2]16, A3= [A/4]16, где [X]16 – остаток от деления целой части числа X на 16 (например, [53/2]16 = 10). Затем было выбрано целое число B такое, что 0 ≤ B ≤ 15. Числа A1, A2, A3 и B записывают в двоичной системе счисления, т.е. представляют каждое из них в виде цепочки из 0 и 1 длины 4, приписывая слева необходимое число нулей. Такие цепочки условимся складывать посимвольно «в столбик» без переносов в следующий разряд согласно правилам: 1+1 = 0+0 = 0 и 1+0 = 0+1 = 1, а саму операцию посимвольного сложения обозначим символом ⊕. Например, 3 ⊕ 14 = (0, 0, 1, 1) ⊕ (1, 1, 1, 0) = (1, 1, 0, 1) = 13. Положим a1 = A1⊕B, a2 = A2⊕B, a3 = A3⊕B. Найдите все возможные значения числа a3, если известно, что a1 = 4, a2 = 10..
Ответ
13 и 5
Вскрытие RSA
Известно, что число 14197777 равно остатку от деления на 56887111 некоторого числа x, возведённого в куб. Числа x и 56887111 имеют общий делитель, отличный от 1, а число56887111 является произведением двух простых чисел. Найдите хотя бы одно такое числоx.
Решение
Пусть y=14197777, N=p·q =56887111, p,q – простые числа. По условиюНОД(x,N)=p>1, то есть x=t·p, где t – натуральное число.
Так как y=rN(x3) - остаток от деления на N числа x3, то НОД(y,N)=p.Вычисляя НОД(14197777, 56887111), находим, что p=10667, тогда y=1331·p, аq=N/p=5333. Делим обе части уравнения
1331·p= rN((t·p)3)
на p, получаем:
1331= rN(t3· p2) = r5333(t3· 106672) = r5333(t3).
Поэтому t = ³√1331 = 11 и x = t·p = 11·10667 = 117337.
Ложь гномов
Для открытия подземелья в волшебной стране надо правильно назвать три целых числа a,b,c, служащих коэффициентами квадратичной функции f(x) = ax2 +bx +c.Представителям четырёх рас были переданы следующие значения функции: троллям –значение f(21), эльфам – f(24), гномам – f(25), оркам – f(28). Когда представители рас встретились, чтобы совместно найти a,b,c, и открыть подземелье, один из представителей, чтобы сорвать мероприятие, предъявил неверное значение. Выясните, кто это был, если известно, что тролли предъявили число 273, эльфы – 357, гномы – 391, орки – 497.
Решение
Разность значений квадратичной функции должна делиться на разность значений аргументов. Проверим выполнение этого факта для различных пар значений:
- для первого и второго: 357–273=84 делится на 3;
- для третьего и четвертого: 497–391=106 не делится на 3; следовательно, значение исказили или гномы, или орки;
- для первого и третьего: 391–273=118 не делится на 4, следовательно, значение исказили тролли или гномы;
- для второго и четвертого: 497–357=140 делится на 4.
Делимость-5
Делится ли число 422008+32009+1991-1 на 385?
Решение
385=5*7*11.
Делится, т.к. число 4k-1 делится на 5 тогда и только тогда, когда k кратно 2, на 7 - тогда и только тогда, когда k кратно 3, на 11 - тогда и только тогда, когда k кратно 5; показатель степени, очевидно, четен.
Далее, число 22008+32009+1991=22008-1+32009+1992 делится на 3, поскольку 2k-1 делится на 3 при четных k и 1992 делится на 3 по известному признаку делимости.
Числа 32009 и 22008 в десятичной записи оканчиваются на 3 и 6 соответственно, поэтому 22008+32009+1991 оканчивается на 0, т.е. делится на 5.
Аффинная перестановка
Для зашифрования сообщения на русском языке его записывают в одну строку без пробелов и знаков препинания. Заглавные буквы заменяются на строчные. В получившейся цепочке буквы нумеруются слева направо 1,2,...,L. Зашифрование происходит путем перестановки букв исходной цепочки по следующему правилу. Фиксируем два натуральных числа a и b. Буква с номером n в исходной цепочке должна в зашифрованной цепочке иметь номер, равный остатку от деления числа a·n+b на L (с одним исключением: если a·n+bнацело делится на L, то остаток полагается равным L). Например, если длина цепочки L=25 и a=9,b=11, то третья буква исходной цепочки будет тринадцатой в зашифрованной цепочке (т.к. 9·13+11=38, а число 38 дает остаток 13 при делении на 25). Известно, что в результате применения этого метода зашифрования к цепочке из 43 букв
светитнезнакомаязвездасновамыоторваныотдома
была получена цепочка
таытоеонсоовзмевтрадазедвмаянтоаысзаимнонвк
При этих же значениях a, b проведено зашифрование еще некоторой цепочки из 28 букв. Получилось вот что:
Видхьврлмаояооаоддсемдроиввоеозтообнзо
Найдите значения a и b и восстановите исходное сообщение.
Решение
Для начала найдём в открытом тексте две уникальные буквы (по возможности близкие). Это например К и Я, стоящие соответственно на 12 и 16 позициях в открытом тексте. В шифрованном тексте они стоят соответственно на 43 и на 28.
Составляем систему уравнений
| { | 12a+b=43k |
| 16a+b=28+43l |
Вычитая, получаем уравнение 4a=28+43m, при m=0 находим a=7, из первого уравнения находим b=2.
Расшифровав второй текст, получим:
Морозвоеводадозоромобходитвладеньясвои
Делимость-4
Делится ли число 222007+32008-2009-1 на 1155?
Решение
Да, делится. Число вида 2k-1 делится на 3 тогда и только тогда, когда k четно, на 5 - тогда и только тогда, когда k кратно 4, на 7 - тогда и только тогда, когда kкратно 3, а на 11 - тогда и только тогда, когда k кратно 10.
Показатель степени 22007+32008-2009 делится на 4; он делится на 3, т.к.
22007+32008-2009= (22007-2006)+(32008-3)= (22007-2-2004)+(32008-3)= 2·(22006-1-1002)+(32008-3)
где 22006-1-1002 делится на 3. Поэтому в соответствии с первыми тремя критериями N делится на 3, 5 и 7. Числа 32008 и 22007 в десятичной записи оканчиваются на 1 и 8 соответственно, поэтому 22007+32008-2009 делится на 10. Таким образом, число N=222007+32008-2009-1 делится на 3·5·7·11=1155.