Колебания, возбужденные в какой-либо точке среды, распространяются в ней с конечной скоростью, зависящей от свойств среды, передаваясь от одной точки среды к другой. Процесс распространения колебаний в сплошной среде называется волновым процессом или волной. При распространении волны частицы среды не движутся вместе с волной, а колеблются около положений равновесия.
Упругими волнами называются механические возмущения, распространяющиеся в упругой среде. Упругие волны бывают продольными и поперечными. В продольных волнах частицы среды колеблются в направлении распространения волны. В поперечных- в плоскостях, перпендикулярных направлению распространения волны. Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны λ. λ = υТ, υ= λ*ν.
Бегущими волнами называются волны, которые переносят в пространстве энергию.
Уравнение колебании частиц, лежащих в плоскости х имеет вид:ξ(x,t)=A cosω(t- 
). В общем случае уравнение плоской волны имеет вид: ξ(x,t)=A cos[ω(t- 
)+φ 
]. Где А- амплитуда волны, ω- циклическая частота, φ - начальная фаза волны.
Согласованное протекание во времени и пространстве нескольких волновых процессов связано с понятием когерентности. Волны называются когерентными если разность их фаз остается постоянной во времени. Наложение в пространстве двух или нескольких когерентных волн в разных его точках получается усиление или ослабление волны в зависимости от соотношения между фазами этих волн. Это явление называется интерференцией волн. Уравнения двух волн:
ξ1 = 
cos[ωt-kr1+φ1], ξ2 =A0/r2cos[ωt-kr2+φ2].
Амплитуда результирующей волны: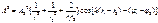 
Результат наложения двух волн зависит от Δ=r1-r2
В точках где k(r1-r2)-(φ1- φ2)= ±2mп наблюдается максимум, а где k(r1-r2)-(φ1- φ2)= ±(2m+1)п- минимум.
Стоячие волны – это волны, образующиеся при наложении двух бегущих волн, распространяющихся навстречу друг другу с одинаковыми частотами и амплитудами.
Предположим две плоских волны распространяются навстречу друг другу.
ξ1=A cos(ωt-kx).
ξ2=A cos(ωt-kx).
Сложив эти уравнения и учитывая, что к=2π получим уравнение стоячей волны: 
Вопрос №8
Постулаты Эйнштейна. Преобразования Лоренца. Релятивистская формула сложения скоростей. Сокращение длин и замедление хода времени в движущихся системах. Интервал.
Эйнштейн заложил основы СТО (специальной теории отнгосит-сти). В основе СТО лежат постулаты:
1. принцип относительности: все законы природы инвариантны по отношению к переходу из одной инерциальной системы отсчета в другую.
2. принцип инвариантности скорости света: скорость света одинакова во всех инерциальных системах отсчета.
Преобразования Галилея заменены преобразованиями Лоренца.
Преобразования Галилея:
Преобразования Лоренца:
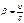
Из преобразований Лоренца вытекает, что при малых скоростях, т.е когда 
<<1, они переходят в классические преобразования Галилея. Из преобразований Лоренца следует сделать вывод, что расстояние и промежуток времени меняются при переходе из одной инерциальной системы отсчета в другую, а в рамках преобразований Галилея они считались абсолютными, не изменяющимися при переходе из одной системы в другую.
Следствия из преобразований Лоренца:
1. Длина тел в разных системах отсчета.
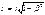
длина стержня, измеренная в системе, относительно которой он движется, оказывается меньше длины измеренной в системе относительно, которой он покоится. Линейные размеры тела уменьшаются в направлении движения.
2. длительность событий.
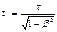
часы, движущиеся относительно инерциальной системы отсчета, идут медленнее покоящихся часов.
3. теорема сложения скоростей.
u – абсолютная скорость относительно неподвижной системы координат
u 
- относительная скорость относительно подвижной системы координат
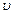- скорость переноса
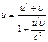
В 4-х мерном пространстве Эйнштейна, в котором каждое событие характеризуется координатами(x,y,z,t), такой величиной является интервал между двумя событиями:
