Распределение Хи-квадрат

Пусть 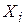– независимые нормированные нормальные случайные величины (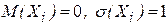, i =1,2, …., n). В этом случае сумма их квадратов 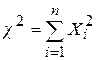имеет распределение Хи-квадрат, параметром которого служит число независимых величин – число степеней свободы.

Если величины 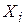связаны дополнительным условием (например, их сумма равна известному числу), то величины уже не будут независимыми, среди них независимыми будут только n– 1 величина.

В общем случае число степеней свободы r равно числу слагаемых минус число наложенных на них условий k, r =n – k.

Число степеней свободы однозначно описывает распределение Хи-квадрат,

плотность распределения Хи-квадрат: ,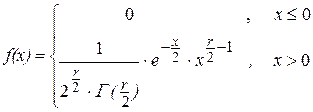

где 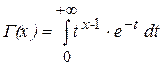– гамма-функция, при 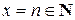Г(n- 1)= n!.

 

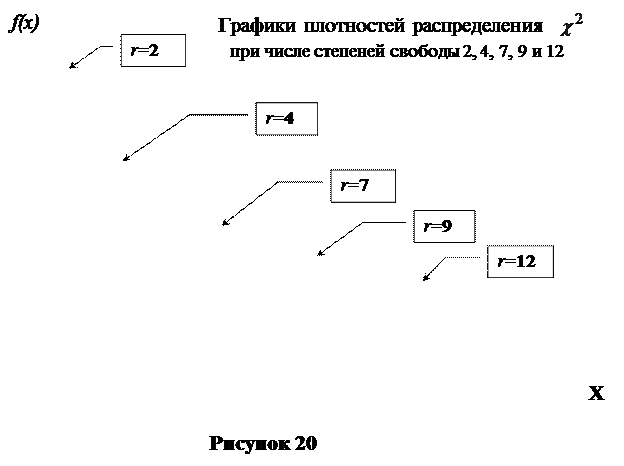
По Рис. 20 видно, что плотность распределения 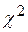при малом числе степеней свободы асимметрична, левосторонняя. При увеличении числа степеней свободы асимметрия уменьшается, распределение 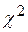медленно приближается к нормальному распределению. После r= 30 и более распределение 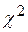можно считать нормальным.

Значения плотности распределения и функции распределения Хи-квадрат вычисляются довольно сложно, для простоты вычислений составлены таблицы, в которых по числу степеней свободы r и уровню значимости 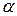указывается критическое значение (квантиль) 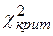, для которого выполняется 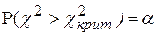( 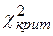– значения аргумента, при которых значение функции распределения равно уровню достоверности ).

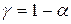Например, при 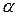=0,05 (т.е. 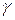=0,95 или 95%) получим зависимость 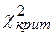от числа степеней свободы :

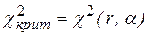r
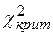
	3,8	6,0	7,8	9,5	11,1	12,6	14,1	15,5	16,9	18,3	19,7	21,0

Более полная таблица приведена в приложении 5, где взято шесть наиболее часто встречающихся значений 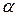(0,01; 0,025; 0,05; 0,95, 0,975; 0,89), число степеней свободы взято до 30. При увеличении числа степеней свободы распределение Хи-квадрат медленно приближается к нормальному распределению.

 

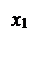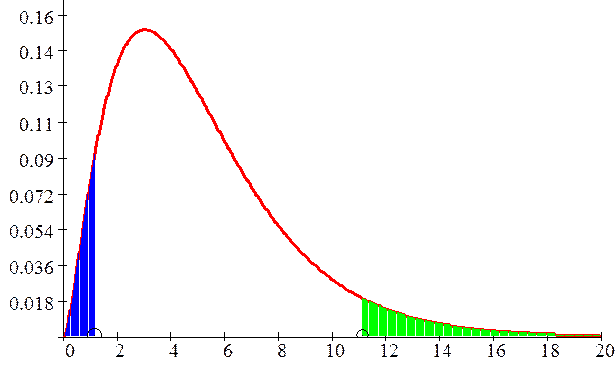
Критические точки легче воспринимаются по графику квантильной функции, обратной для функции распределения. Квантильная кривая строится так: по оси абсцисс откладывают вероятности, по оси ординат откладывают значения исследуемой величины и график показывает зависимость значений случайной величины 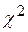от указанной вероятности.

 

Квантильные функции распределения Хи-квадрат

при числе степеней свободы r =1, 3, 5, 7, 9, 15, 20, 30

 

 

Чтобы получить критическую точку (квантиль) при известном числе степеней свободы r и вероятности р (уровне значимости 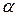=1– р) необходимо

· Отложить 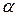на оси абсцисс;

· Найти соответствующую точку графика (восстановив перпендикуляр до пересечения с графиком);

· Спроецировать точку графика на ось ординат, получить критическую точку .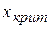

Аналогичные действия, но в обратном порядке, выполняются при нахождении вероятности принимать значения, меньшие выбранного .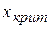

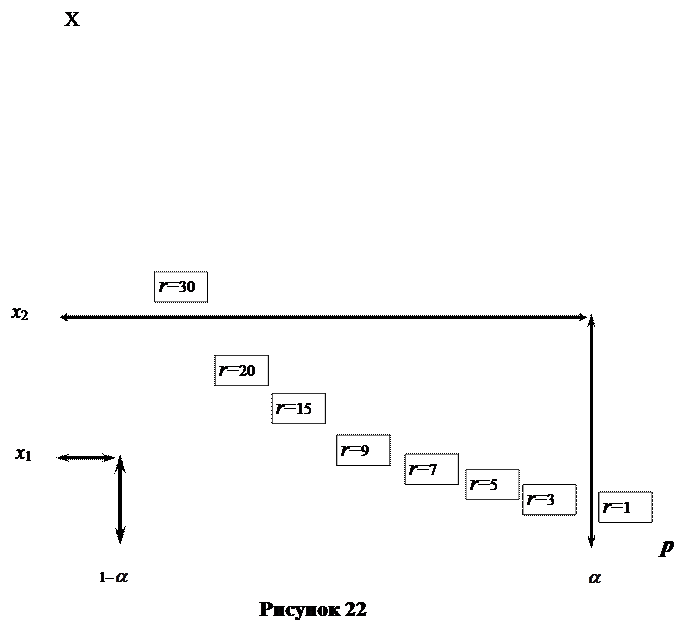
На Рис.22 показано нахождение критических точек распределения 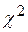при числе степеней свободы r =15 и вероятностях (уровнях значимост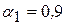и) и .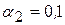

По рисунку 22 видно, что для случайной величины Х, имеющей распределение Хи-квадрат при r =15 выполнено:

а) Х принимает значения, меньше 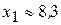, с вероятностью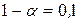

(принимает значения, больше 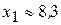, с вероятностью 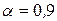или 90%); б) Х принимает значения, меньше 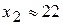, с вероятностью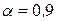

(принимает значения, больше 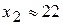, с вероятностью );

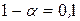в) Вероятность получить значение Х в пределах от 8 до 22 равна разности значений функции распределения в точках х =22 и х =8 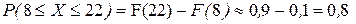т.е. составляет около 80%.

 

Аналогично можно оценить критические точки и значения функции распределения для различных уровней достоверности, не перечисленных в таблице приложения 5, но изображенные на Рис. 22.

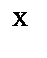
Распределение Стьюдента

Пусть имеется нормально распределённая случайная величина U с параметрами 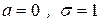(нормированная) и случайная величина V, независимая с U и имеющая распределение Хи-квадрат с r степенями свободы. В таком случае говорят, что случайная величина 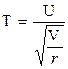имеет распределение Стьюдента, называемое t –распределением (Стьюдент – псевдоним английского учёного В. Госсета).

Плотность распределения Стьюдента ,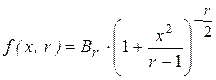

где .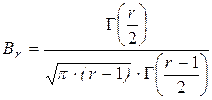

 

Распределение Стьюдента однозначно описывается числом степеней свободы r.

На Рис.23 показаны плотности распределение Стьюдента при числе степеней свободы 1, 3 и 50.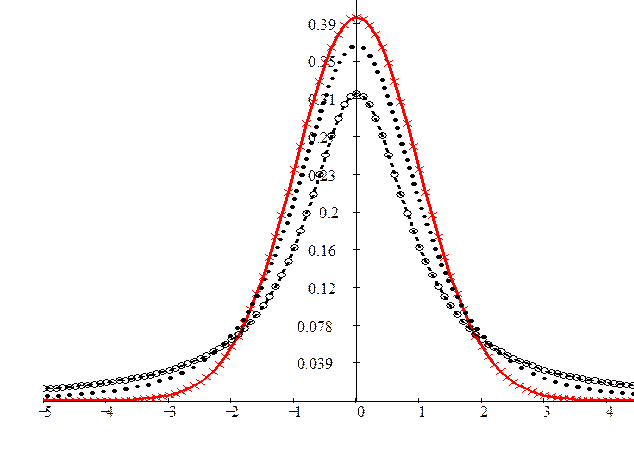

По рисунку 23 видно, что плотность распределения Стьюдента симметрична относительно оси ординат, является чётной. Для неё 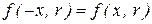, 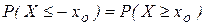. При необходимости вычислить вероятность симметричного отклонения Т от нуля используют чётность, 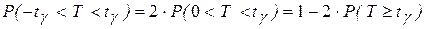, где 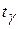– критическая точка распределения Стьюдента для двусторонней области.

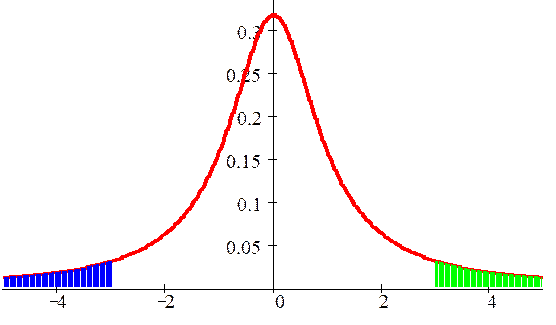
Правосторонняя и левосторонняя критические области с уровнями значимости 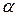и 1- 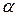имеют симметричные относительно нуля критические точки. Двусторонняя область является объединением двух односторонних областей – заштрихованная часть оси Ох на Рис. 24 (либо дополнением их объединения до числовой прямой – не заштрихованная часть оси Ох на Рис. 24). Критические точки (квантили) распределения Стьюдента можно найти по таблице приложения 7 (двусторонняя область имеет в 2 раза больший уровень значимости, чем для односторонней области). Для двусторонней критической области, для которо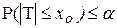й или 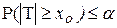, критические точки симметричны относительно начала координат. Правую критическую точку 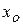двусторонней области 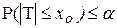(и симметричную ей точку - 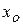) можно найти как критическую точку односторонней области, из условия .

 

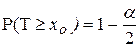Распределение Стьюдента при увеличении степеней свободы приближается к нормальному нормированному распределению с плотностью распределения 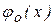. При достаточно небольшом числе степеней свободы плотность распределения Стьюдента более пологая, чем нормальная кривая.

 

Критические точки распределения Стьюдента легче воспринимаются по графику квантильной функции, обратной для функции распределения. Для неё на оси абсцисс откладывают вероятности, по оси ординат откладывают значения исследуемой величины и график показывает зависимость значений случайной величины 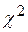от указанной вероятности.

 

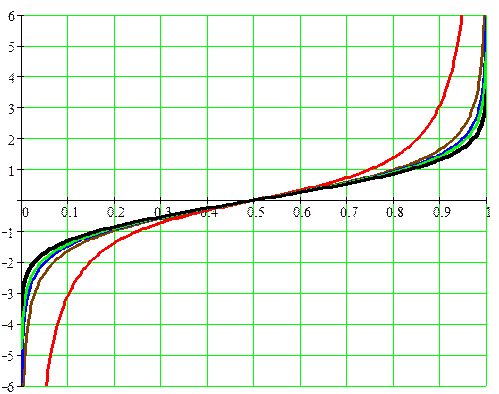
Графики квантильных функций 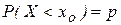проходят через точку р =0,5 при Х =0, симметричны относительно этой точки из-за симметричности плотности распределения относительно оси ординат, что изображено на Рис 25а.

Для большей точности рассмотрим поведение квантильных функций в окрестности р =1, изобразив графики зависимости 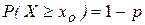при различных числах степеней свободы. С помощью таких кривых можно найти критическую точку 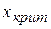правосторонней области по заданному уровню значимости 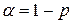(см. Рис. 25б). Часть таких значений можно найти по таблице приложения 7, зафиксировав 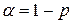в нижней строке (односторонней области) и в первом столбце взяв число степеней свободы. Правило использования графика квантильной функции приведено выше в 5.2.4.

 

Квантильные функции для распределения Стьюдента

r =30

r =20

r =15

r =9

r =7

r =5

r =3

r =1

Рисунок 25а

r =7

r =30

r =12

r =9

r =5

r =3

r =2

r =1

при числе степеней свободы r

 

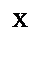
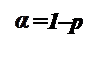
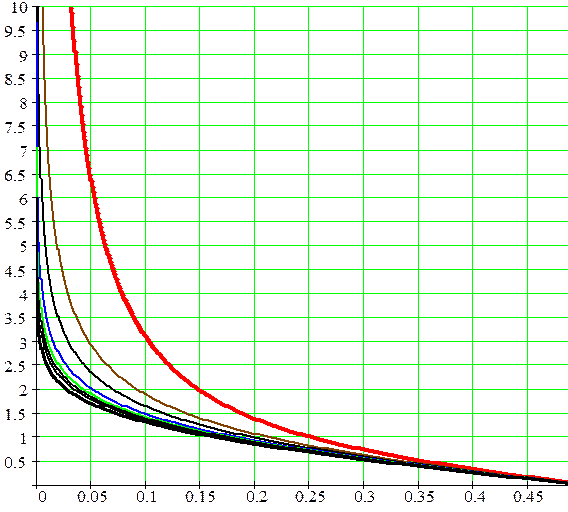
Чтобы получить критическую точку (квантиль) при известном числе степеней свободы r и вероятности =1– р (уровне значимости) необходимо

· Отложить на оси абсцисс;

· Найти соответствующую точку графика (восстановив перпендикуляр до пересечения с графиком);

· Спроецировать точку графика на ось ординат, получить 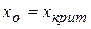– критическую точку правосторонней области .

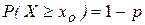· Критическая точка левосторонней области 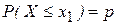находится из четности т.е. .

 

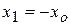Аналогичные действия, но в обратном порядке, выполняются при нахождении вероятности принимать значения, меньшие выбранного .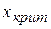

На Рис.25 показано нахождение критических точек распределения при различных числах степеней свободы r и вероятностях (уровнях значимости) 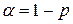. При увеличении уровня достоверности 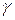(уменьшении уровня значимости 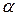) и постоянном числе степеней свободы происходит увеличение 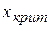(расширение двусторонней критической области). При неизменном уровне значимости и возрастании числа степеней свободы происходит уменьшение 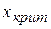(сужение двусторонней критической области).