Принцип Дирихле
Андреев А.A., Савин А.Н., Саушкин М.Н.
Введение
При решении многих задач используется логический метод рассуждения — "от противного". В данной брошюре рассмотрена одна из его форм — принцип Дирихле. Этот принцип утверждает, что если множество из N элементов разбито на пнепересекающихся частей, не имеющих общих элементов, где N>n то, по крайней мере, в одной части будет более одного элемента. Принцип назван в честь немецкого математика Дирихле (1805-1859), который успешно применял его к доказательству арифметических утверждений.
По традиции принцип Дирихле объясняют на примере "зайцев и клеток". Если мы хотим применить принцип Дирихле при решении конкретной задачи, то нам предстоит разобраться, что в ней — "клетки", а что — "зайцы". Это обычно является самым трудным этапом в доказательстве. Цель этого статьи — познакомить школьника с некоторыми изюминками решения задач на принцип Дирихле.
Статья предназначена главным образом для старшеклассников, однако школьники младших классов также несомненно найдут в ней много полезного.
Формулировка принципа Дирихле
Самая популярная формулировка принципа Дирихле звучит так:
ФОРМУЛИРОВКА 1. "Если в n клетках сидит n+1 или больше зайцев, то найдётся клетка, в которой сидят по крайней мере два зайца".
Заметим, что в роли зайцев могут выступать различные предметы и математические объекты - числа, отрезки, места в таблице и т. д.
Принцип Дирихле можно сформулировать на языке множеств и отображений.
ФОРМУЛИРОВКА 2. "При любом отображении множества P, содержащего n+1 элементов, в множество Q, содержащее n элементов, найдутся два элемента множества P, имеющие один и тот же образ".
Несмотря на совершенную очевидность этого принципа, его применение является весьма эффективным методом решения задач, дающим во многих случаях наиболее простое и изящное решение. Однако во всех этих задачах часто нелегко догадаться, что считать "зайцем", что - "клеткой", и как использовать наличие двух "зайцев", попавших в одну "клетку". С помощью принципа Дирихле обычно доказывается существование некоторого объекта, не указывая, вообще говоря, алгоритм его нахождения или построения. Это даёт так называемое неконструктивное доказательство - мы не можем сказать, в какой именно клетке сидят два зайца, а знаем только, что такая клетка есть.
Приводимые ниже теоремы и задачи показывают, что природа "зайцев" и "клеток" в различных задачах может сильно отличаться друг от друга.
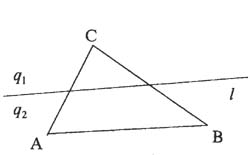
Пример 1. Доказать, что если прямая l, расположенная в плоскости треугольника ABC, не проходит ни через одну из его вершин, то она не может пересечь все три стороны треугольника.
Решение
|
Полуплоскости, на которые прямая l разбивает плоскость треугольника ABC, обозначим через q1 и q2; эти полуплоскости будем считать открытыми (то есть не содержащими точек прямой l). Вершины рассматриваемого треугольника (точки A, B, C) будут "зайцами", а полуплоскости q1 и q2 - "клетками". Каждый "заяц" попадает в какую-нибудь "клетку" (ведь прямая l не проходит ни через одну из точек A, B, C). Так как "зайцев" три, а "клеток" только две, то найдутся два "зайца", попавшиев одну "клетку"; иначе говоря, найдутся такие две вершины треугольника ABC, которые принадлежат одной полуплоскости. См рисунок.
Пусть, скажем, точки A и B находятся в одной полуплоскости, то есть лежат по одну сторону от прямой l. Тогда отрезок AB не пересекается с l. Итак, в треугольнике ABC нашлась сторона, которая не пересекается с прямой l.
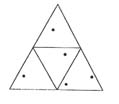
Пример 2. Внутри равностороннего треугольника со стороной 1 расположено 5 точек. Доказать, что расстояние между некоторыми двумя из них меньше 0,5.
Решение
|
Средние линии правильного треугольника со стороной 1 разбивают его на четыре правильных треугольничка со стороной 0,5. Назовём их "клетками", а точки будем считать "зайцами". По принципу Дирихле из пяти точек хотя бы две окажутся в одном из четырёх треугольничков (См. рисунок). Расстояние между этими точками меньше 0,5, поскольку точки не лежат в вершинах треугольничков. (Здесь использована известная лемма о том, что длина отрезка, расположенного внутри треугольника, меньше длины его наибольшей стороны.)
Пример 3. На краю круглого стола расположены на одинаковом расстоянии друг от друга n флагов стран, за столом сидят n послов этих стран, причём каждый посол сидит рядом с чужим флагом. Доказать, что существует такое вращение стола, после которого хотя бы два посла окажутся рядом с флагом своей страны.
Решение Существует n-1 способов вращения стола, после каждого из них взаимное расположение флагов и послов изменится. Каждому послу сопоставим вращение, после которого он окажется рядом со своим флагом. Согласно принципу Дирихле при каком-то вращении два (может, и больше) посла окажутся рядом со своим флагом. В решении задачи роль "зайцев" играют, естественно, послы, а роль "клеток" - положения стола при различных вращениях. Посол попадает в "клетку", если при соответствующем этой "клетке" вращении стола он оказывается рядом с флагом своей страны. Таким образом, "клеток" у нас n-1, а "зайцев" - n. Замечание Условие о том, что вначале ни один из послов не находится рядом со своим флагом, существенно. На самом деле первоначальное положение также является "клеткой", но эта "клетка" по условию заведомо окажется пустой. Так что можно считать, что всего "клеток" имеется n-1.
Пример 4. Доказать, что для любого действительного числа a > 0 и любого натурального N найдутся такие целые m і 0 и k > 0, что |ka-m| Ј1/N.
Решение Разобьём отрезок [0, 1] точками 1/N, 2/N,..., [(N-1)/(N)] на N отрезков (См. рисунок). Полученные отрезки будем считать "клетками", а числа 1, 2,..., N+1 примем в качестве "зайцев".
Если k - один из "зайцев", то число ka можно записать в виде ka = m + x, где m - целое, 0Ј x < 1 (т. е. в виде суммы целой и дробной части). Число x попадает в одну из "клеток"; в эту "клетку" мы и посадим "зайца" k.
Так как "зайцев" больше, чем "клеток", то найдутся два "зайца", сидящих в одной "клетке". Иначе говоря, среди чисел 1, 2,..., N+1 найдутся такие два числа k1 < k2, что
|
|
причём x1 и x2 находятся в одной "клетке", и поэтому |x2-x1| Ј 1/N.
Таким образом,
|
то есть числа k = k2 - k1 и m = m2 - m1 являются искомыми. Здесь k > 0, так как k2 > k1, и m і 0, так как k2a - k1a = (m2 + x2) - (m1 + x1) > 0, откуда m2 - m1 > x1 - x2 > -1 (ведь 0 Ј x1 < 1 и 0 Ј x2 < 1), и поскольку m1 и m2 - целые числа, m2 - m1 і 0.
Пример 5. На клетчатой бумаге отметили 5 точек, расположенных в узлах клеток. Доказать, что хотя бы один из отрезков, соединяющих эти точки, проходит через узел клетки.
Решение Введём на клетчатой бумаге систему координат с началом координат в одном из узлов, осями, направленными вдоль линий сетки, и единичным отрезком, равным стороне клетки. Тогда все отмеченные точки будут иметь целочисленные координаты. Покажем, что найдутся две точки из пяти, у которых одна и та же чётность координат x и координат y. "Зайцами" у нас будут точки, а "клетками" - пары (Ч, Ч), (Ч, Н), (Н, Ч), (Н, Н). Если, например, у точки (x, y) координата x чётна, а координата y нечётна, то мы её поместим в "клетку" (Ч, Н). Итак, 5 "зайцев" и 4 "клетки". Пусть (x1, y1) и (x2, y2) - две точки, попавшие в одну "клетку". Середина отрезка, соединяющего эти две точки, имеет координаты ([(x1+x2)/ 2], [(y1+y2)/ 2]), которые являются целыми числами в силу одинаковой чётности x1 и x2, y1 и y2. Таким образом, середина этого отрезка лежит в узле сетки, т.е. данный отрезок является искомым.
Пример 6. На длинной прямолинейной дороге с равными интервалами вырыты небольшие поперечные канавки (См. рисунок). Расстояние между центрами каждых двух соседних канавок равно Ц2 метров. Доказать, что какими бы узенькими эти канавки ни были сделаны, человек, шагающий по дороге и имеющий длину шага 1 метр, рано или поздно попадёт в одну из канавок.
Решение Представим, что мы можем "намотать" дорогу на барабан, длина окружности которого равна Ц2 метров. Тогда все канавки на этом барабане совместятся, а каждый шаг человека будет изображаться на окружности дугой длины 1 метр. Будем последовательно отмечать на окружности след человека после первого, второго, третьего и так далее шагов. Нам надо доказать, что хотя бы один из этих следов попадёт внутрь заданной на окружности дуги, изображающей канавку, какой бы малой ни была длина h этой дуги. Нетрудно понять, что если нам удастся найти такие k и m, для которых следы k-го и (k+m)-го шагов удалены друг от друга (на окружности) меньше чем на h, то требуемое утверждение докажется легко. Ведь ещё после m шагов новый след (то есть (k+2m)-й) опять сдвинется на расстояние меньшее h, затем мы рассмотрим следующие m шагов и так далее. Ясно теперь, что, сделав несколько раз по m шагов, мы неминуемо обнаружим след, попавший в канавку (потому что, перемещаясь на одно и то же расстояние, меньшее h, нельзя "перешагнуть" канавку ширины h). Итак, нужно найти два следа, находящиеся на окружности на расстоянии, меньшем h. Вот здесь-то и помогают "зайцы". Действительно, разделим окружность на дуги, каждая из которых имеет длину меньше h; эти дуги мы и назовём "клетками". Пусть их имеется p штук. Если мы возьмём число следов большее, чем p (заметим, что никакие два следа не совпадут в силу иррациональности числа Ц2), то по принципу Дирихле хотя бы в одну из клеток попадёт более одного следа ("зайца"). Расстояние между двумя следами, попавшими в одну "клетку", меньше h; этим наше утверждение и доказано.
В ряде задач применяют следующее обобщение принципа Дирихле.
ФОРМУЛИРОВКА 3. "Если nk+1 зайцев размещены в n клетках, то найдутся k+1 зайцев, которые посажены в одну клетку (n, k - натуральные числа)".
Обобщенный принцип Дирихле также достаточно очевиден: если бы в каждой клетке сидело не более k зайцев, то во всех клетках было бы не более nk зайцев, что противоречит условию. Обобщение принципа используют, когда требуется выявить несколько (три и более) объектов, обладающих некоторым свойством. Разберём несколько примеров.
Пример 7. В прямоугольнике 5×6 закрашено 19 клеток. Докажите, что в нём можно выбрать квадрат 2×2, в котором закрашено не менее трёх клеток.
Решение

|
Разделим прямоугольник на 6 частей по 5 клеток (Cм. рисунок). Согласно принципу Дирихле в одной из этих частей будет закрашено не менее 4 клеток. Тогда в квадрате 2×2, содержащемся в этой части, закрашено либо 3, либо 4 клетки. Это и будет искомый квадрат.
Пример 8. В классе 25 человек. Известно, что среди любых трёх из них есть двое друзей. Докажите, что есть ученик, у которого не менее 12 друзей.
Решение Выберем любых двух учеников класса, которые не дружат между собой. (Если таких нет, то все ученики класса дружат между собой, значит, у каждого имеется 24 друга, и задача решена.) Из оставшихся 23 учеников каждый дружит с одним из этих двух, иначе мы имели бы тройку учеников, среди которых не было бы друзей. Тогда у одного из выбранных двух учеников не менее 12 друзей. (23 "зайца" рассажены в двух "клетках".)
Пример 9. В единичный квадрат бросили 51 точку. Доказать, что какие-то три из них можно накрыть кругом радиуса 1/7.
Решение Разобьём данный квадрат на 25 одинаковых квадратиков ("клеток") со стороной 1/5. В один из них попадёт не менее трёх точек ("зайцев"). Окружность, описанная около квадратика со стороной 1/5, имеет радиус 1/5·[(Ц2)/ 2] = [1/([Ц50])] < [1/([Ц49])] = 1/7, поэтому этот квадратик можно накрыть кругом радиуса 1/7.