Глава 4. Корреляционно-регрессионный анализ.

 

§1. Корреляционная зависимость. Две основные задачи теории корреляций.

 

Во многих задачах требуется установить и оценить зависимость одной случайной величины от другой случайной величины. Мы будем рассматривать зависимость случайной величины Y от случайной величины X.

Две случайные величины X и Y могут быть связаны функциональной зависимостью, статистической зависимостью, либо быть независимыми.

Статистическая зависимость.

Статистической зависимостью называется зависимость, при которой изменение одной случайной величины влечёт изменение распределения другой случайной величины. Статистическую зависимость называют корреляционной, если изменение одной случайной величины изменяет среднее значение другой.

Пример.

Y – урожай; X – количество внесённых удобрений.

Y не является функцией от X, однако изменение X изменяет среднее значение Y, т.е. среднее значение Y является функцией от X. Y связано с X корреляционной зависимостью.

Определение. Условным средним называют среднее арифметическое значений случайной величины Y, соответствующих значению X = x.

Если каждому X соответствует одно и только одно значение , то условное среднее является функцией от x.

(1)

Функциональная зависимость называется корреляционной зависимостью Y от X.

Уравнение (1) – уравнение регрессии Y на X.

Функцию f(x) называют регрессией Y на X, а график функции f(x) называют линией регрессии Y на X.

Аналогично, 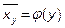- регрессия X на Y.

График функции называется линией регрессии X на Y.

1-я задача теории корреляции.

Установить вид функции регрессии (линейная, квадратичная, показательная и т.д.). Если обе функции регрессии f(x) и φ(y) линейны, то корреляцию называют линейной, в противном случае – нелинейной. При линейной корреляции обе линии регрессии линейны.

2-я задача теории корреляции.

Оценить тесноту корреляционной зависимости. Теснота корреляционной зависимости Y от X оценивается по величине рассеяния значений Y вокруг условного среднего . Большое рассеяние говорит о слабой зависимости Y от X, либо об её отсутствии. Малое рассеяние указывает на наличие достаточно сильной зависимости. Возможно даже, Y и X связаны функционально, но под воздействием второстепенных случайных факторов эта связь оказалась размытой, и поэтому при одном и том же значении X = x величина Y принимает различные значения.

 

§2. Выборочное уравнение линейной регрессии.

 

Под уравнением регрессии мы понимаем зависимость между переменной X и условным средним значением переменной Y.

(1) – уравнение регрессии

Если функция регрессии – линейная, то говорят о линейной регрессии. Модель линейной регрессии является наиболее распространённым и простым видом зависимости между экономическими показателями.

C=C₀+bI, где C – частное потребление, С₀ – автономное потребление, I – доход домохозяйств, b – предельная склонность к потреблению.

Различают теоретическое линейное уравнение регрессии и выборочное линейное уравнение регрессии.

Теоретическое линейное уравнение регрессии: Y=α+ β X+ε, где α и β - теоретические параметры (коэффициенты регрессии), X – объясняющая переменная (регрессор), Y – объясняемая переменная.

В случае, когда уравнение записывается для двух случайных величин, говорят о парной регрессии.

ε – случайное отклонение, это связано с тем, что при одном и том же значении X могут быть различные значения Y.

Основные причины присутствия в регрессионных моделях случайного отклонения ε.

1. Невключение в модель всех объясняющих переменных.

2. Возможная нелинейность модели.

3. Ошибки измерений.

4. Ограниченность статистических данных.

Для определения значений теоретических коэффициентов регрессии α и β необходимо знать и использовать все значения переменных X и Y в генеральной совокупности, что практически невозможно (дорого).

Задачи регрессионного линейного анализа состоят в том, чтобы по имеющимся статистическим данным выборки (x_i,y_i), i=1,2,…,n из генеральной совокупности всех возможных значений X и Y:

1. Получить наилучшие оценки параметров α и β.

2. Проверить статистические гипотезы о параметрах модели.

3. Проверить, достаточно ли хорошо согласуется модель со статистическими данными (адекватность модели в данном наблюдении).

Таким образом, по выборке ограниченного объёма i=1,2,…,n мы сможем построить выборочное (эмпирическое) уравнение регрессии.

Выборочное уравнение линейной регрессии.

(2) , где - расчётное значение, оценка условного математического ожидания .

Изобразим на плоскости XOY выборочные точки и прямую линию регрессии.

(x_i,y_i), i=1,2,…,n

Эта прямая не проходит через точки наблюдений. Для каждой наблюдаемой точки можно указать её отклонение от линии регрессии.

- отклонение, где y_i – значение переменной Y в i -м наблюдении, а - значение переменной Y, рассчитанное по уравнению регрессии (2) при x=x_i: .

Оценка коэффициентов регрессии методом наименьших квадратов.

Пусть по конкретной выборке (x_i,y_i), i=1,2,…,n требуется определить оценки a и b – неизвестных параметров теоретического распределения α и β. Для получения этих оценок будем использовать МНК: подбираются такие значения a и b, при которых сумма квадратов отклонений фактических значений y_i от минимальна.

,

Т.е. мы будем находить параметры a и b по:

; ; поделим 2 уравнения на n:

Мы получили линейную алгебраическую систему относительно a и b.

;

Из 1-го уравнения последней системы:

; ; ;

Выводы:

1. Оценки МНК являются функциями от выборки, что позволяет легко их рассчитывать.

2. Оценки МНК являются точечными оценками теоретических коэффициентов регрессии α и β.

3. Согласно формуле , выборочная прямая регрессии проходит через точку .

4. Выборочное уравнение регрессии построено так, что и (среднее значение отклонений равно нулю).

Действительно, из уравнения .

МНК является наиболее простым с вычислительной точки зрения, кроме того, оценки коэффициентов регрессии, найденные МНК, при выполнении условий Гаусса-Маркова обладают рядом оптимальных свойств:

1. Состоятельность.

2. Несмещённость.

3. Эффективность.

Кроме МНК существуют и другие методы для нахождения коэффициентов регрессии (метод моментов и метод наибольшего правдоподобия).

Проверка статистических гипотез по параметрам модели.

При проверке качества построенного уравнения регрессии, прежде всего, проверяется наличие линейной зависимости между Y и X. Для этого проверяется гипотеза:

H₀:b=0 (нет линейной зависимости между Y и X).

H₁: b≠0 (есть линейная зависимость).

В качестве статистического критерия проверки гипотезы применяется , где S_b – стандартная ошибка определения коэффициента b.

; , где S² – несмещённая оценка дисперсии случайных отклонений .

По выборочным данным рассчитывается статистика t_b, и сравниваем её с t_кр (находим t_кр по таблице распределения Стьюдента): , где α – уровень значимости, (n-2) – число степеней свободы.

Критическая область в данном случае является двусторонней, т.к. нам нужно именно отличие коэффициента b от нуля (он может быть больше или меньше нуля).

Если , то мы попали в критическую область, т.е. гипотеза H₀ отклоняется, и мы считаем, что существует линейная зависимость между Y и X, и коэффициент b является статистически значимым.

В противном случае гипотеза H₀ принимается, и мы приходим к выводу о том, что есть основании считать, что линейная связь между Y и X отсутствует. Аналогично, на основании статистики проверяется гипотеза о статистической значимости коэффициента a.

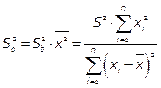
Выборочное значение статистики t_a сравнивается с t_кр, и делаем вывод о статистической значимости или незначимости коэффициента a.

Для подтверждения статистической значимости коэффициента линейного уравнения регрессии строят интервальные оценки коэффициентов α и β теоретического уравнения линейной регрессии по их точечным оценкам a и b.

;

Эти доверительные интервалы накрывают неизвестные значения параметров α и β с вероятностью γ =1- α. Если внутрь доверительного интервала попадает нуль, т.е. нижняя граница доверительного – отрицательна, а верхняя – положительна, то оцениваемый параметр принимается равным нулю, т.к. он не может быть одновременно и положительным и отрицательным.

Проверка общего качества уравнения линейной регрессии. Коэффициент детерминации R².

Общее качество уравнения регрессии оценивается по тому, как хорошо выборочное уравнение регрессии согласуется с выборочными данными, т.е. насколько широко рассеяны точки наблюдений относительно прямой линии регрессии. Суммарной мерой общего качества уравнения регрессии является коэффициент детерминации R².

- отклонение

;

Возведём обе части равенства в квадрат, и просуммируем по всему объёму выборки:

Покажем, что удвоенное произведение правой части равно нулю:

- общая сумма квадратов отклонений – мера общего разброса переменной Y относительно .

- сумма квадратов отклонений, обусловленная регрессией – мера разброса, объяснённая формулой .

- остаточная сумма квадратов отклонений – мера разброса точек наблюдений около линии регрессии, не объяснённая уравнением регрессии.

Введём величину - коэффициент детерминации, он показывает долю разброса значений переменной y, объяснённую регрессией Y на X в общей дисперсии результативного признака.

Из этой формулы видно, что чем теснее линейная связь между X и Y, тем ближе значение R² к единице; чем слабее эта связь, тем ближе R² к нулю.

Можно показать, что R² выражается через коэффициент корреляции: .

Оценивание общего качества уравнения регрессии состоит в проверке гипотезы о статистической значимости R².

H₀: R²=0

H₁: R²≠0

Критерий проверки - , n – объём выборки. Эта статистика имеет распределение Фишера. По выборочным данным рассчитываем , и сравниваем с . Если F_кр > F_в, то H₀ не отклоняется и признаётся статистическая незначимость, ненадёжность уравнения регрессии.