§1. Основные понятия.
Статистическая гипотеза – это некоторое предположение относительно генеральной совокупности, проверяемое по выборочным данным.
Примеры статистических гипотез:
1. Нормально распределённая случайная величина X имеет генеральную среднюю a, равную a0 – H0: a = a0.
2. Нормально распределённая случайная величина X имеет дисперсию σ2, равную σ2 – Н0: σ2 =  .
.
3. Выборка x =(x1, x2, …, xn) извлечена из нормально распределённой генеральной совокупности.
Различают гипотезы параметрические и непараметрические.
Гипотеза называется параметрической, если в ней содержится утверждение о параметре распределения известного вида.
Гипотеза называется непараметрической, если она выдвигает утверждение о виде неизвестного закона распределения случайной величины.
Гипотеза, которую следует проверить, называется основной или нулевой гипотезой H0. Вместе с нулевой гипотезой рассматривают конкурирующую или альтернативную гипотезу H1. Эта гипотеза является отрицанием нулевой гипотезы.

Параметрическая гипотеза называется простой, если она содержит предположение равно об одном значении параметра.
H0: λ =5 – параметр показательного распределения λ
H0: X – нормально распределённая случайная величина
a = a0, σ известна
Параметрическая гипотеза называется сложной, если она состоит из конечного или бесконечного множества простых гипотез.
H0: X – нормально распределённая случайная величина
a = a0, σ неизвестна
Статистику, значение которой находят по выборке, и по этому значению выносят решение: принять или не принять основную гипотезу, называют статистическим критерием. При этом используют правило, которое устанавливает, при каких числовых значениях статистики нулевая гипотеза принимается, а при каких – нет.
Схема проверки гипотезы.
Всё множество возможных значений статистики делится на два непересекающихся подмножества:
Область S – область отклонения основной гипотезы
Область  - область принятия основной гипотезы
- область принятия основной гипотезы
Область S называется критической. Если вычисленное по выборке значение статистики попадает в область S, то нулевая гипотеза H0 отклоняется. Если вычисленное по выборке значение статистики попадает в область  , то нулевая гипотеза H0 принимается.
, то нулевая гипотеза H0 принимается.
В итоге статистической проверки гипотезы могут иметь место ошибки двух родов:
1. Ошибка 1-го рода – будет отвергнута правильная гипотеза H0. Вероятность ошибки 1-го рода – α,  , где α – уровень значимости. Обычно в качестве α берётся 0,1; 0,05; 0,01; 0,005.
, где α – уровень значимости. Обычно в качестве α берётся 0,1; 0,05; 0,01; 0,005.
2. Ошибка 2-го рода состоит в том, что будет принята неправильная гипотеза H0. Вероятность этого события – β,  ,
,  . Число (1-β) – мощность критерия. Геометрически мощности критерия – вероятность попадания в критическую область, когда гипотеза неверна.
. Число (1-β) – мощность критерия. Геометрически мощности критерия – вероятность попадания в критическую область, когда гипотеза неверна.
Пример.
Завод выпускает лампочки нового типа и предполагаем, что средний срок службы таких ламп будет не менее 1500 часов. Для выборки из 80 ламп оказалось, что средний срок службы ламп равен 1475 часов. Среднее квадратическое отклонение σ известно и σ =100 часов. Проверить гипотезу, выдвинутую фирмой при уровне значимости α =0,1 и построить график функции 1-β=(1-β)(a). Считать, что X – срок службы – нормально распределённая случайная величина.
Решение.
Ho: a0 =1500
H1: a0 = a1 <1500
(Случай a >1500 нас не интересует, т.к. какие-либо действия следует принимать, если срок службы лампочек <1500 ч).

При такой гипотезе H1 критическая область является левосторонней.
 Вероятность ошибки I -го рода – площадь по графиком нормального распределения выборочной средней слева от левосторонней критической границы. Найдём эту границу
Вероятность ошибки I -го рода – площадь по графиком нормального распределения выборочной средней слева от левосторонней критической границы. Найдём эту границу  ;
;  . По таблице нормального распределения U2α =1,28.
. По таблице нормального распределения U2α =1,28. 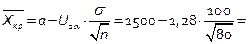
 .
.
Найденное по выборке значение статистики  , нулевая гипотеза H0 отвергается. Говорят: средний срок службы лампочек значимо меньше 1500 часов.
, нулевая гипотеза H0 отвергается. Говорят: средний срок службы лампочек значимо меньше 1500 часов.
Построим график функции 1-β=(1-β)(a).
 Предположим, что нулевая гипотеза неверна и a =1490. (1-β) – вероятность попасть в критическую область S, т.е. получить
Предположим, что нулевая гипотеза неверна и a =1490. (1-β) – вероятность попасть в критическую область S, т.е. получить 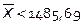 . Следовательно, (1-β) – площадь под графиком распределения выборочной средней при a =1490 левее 1485,69. Эта площадь –
. Следовательно, (1-β) – площадь под графиком распределения выборочной средней при a =1490 левее 1485,69. Эта площадь –

Возьмём другое значение a =1480. 
 (площадь под графиком левее 1485,69).
(площадь под графиком левее 1485,69).
 Если a =1430, то
Если a =1430, то  =0,5+Φ(4,98)=0,5+0,499=0,999.
=0,5+Φ(4,98)=0,5+0,499=0,999.
График функции 1-β=(1-β)(a) имеет вид (a =1500, 1-β= α =0,1):

Мы построили график функции мощности в случае левосторонней критической границы.
 Если критическая граница будет правосторонней, то график функции будет симметричным графику для левосторонней критической границы относительно вертикали a0.
Если критическая граница будет правосторонней, то график функции будет симметричным графику для левосторонней критической границы относительно вертикали a0.
В случае двусторонних критических границ график выглядит следующим образом:

Свойства мощности критерия (1-β).
Мощность зависит от расстояния между a0 и действительным значением a, среднего квадратического отклонения генеральной совокупности, размера выборки и уровня значимости.
1. Чем больше расстояние между a0 и действительным значением a, тем больше вероятность заметить неверность нулевой гипотезы.
2. Чем меньше σ – среднее квадратичекое отклонение генеральной совокупности, тем больше мощность критерия.
3. Чем больше размер выборки, тем больше мощность критерия.
4. Чем меньше уровень значимости, тем меньше мощность критерия.
§2. Гипотеза о равенстве выборочной средней и гипотетического математического ожидания нормального распределения.
Случайная величина X имеет нормальное распределение. a – неизвестно, но есть основание предполагать, что a=a0.
1. σ2 – известна.
Пусть из генеральной совокупности извлечена объёма n. Требуется проверить нулевую гипотезу
H0: a = a0
H1: a ≠ a0
В качестве статистического критерия возьмём  .
.
При использовании этой статистики область принятия гипотезы задаётся неравенством  , (*)
, (*)
область отклонения (двусторонняя критическая область) имеет вид  .
.
По выборке вычисляется  . Если это значение удовлетворяет неравенству (*), то гипотеза H0 принимается, в противном случае H0 отклоняется.
. Если это значение удовлетворяет неравенству (*), то гипотеза H0 принимается, в противном случае H0 отклоняется.
H0: a = a0
H1: a=a1>a0
В этом случае критическая область – правосторонняя:  . Область принятия гипотезы:
. Область принятия гипотезы: 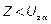 .
.
H0: a = a0
H1: a=a1<a0
В этом случае критическая область – левосторонняя: 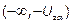 . Область принятия гипотезы:
. Область принятия гипотезы:  .
.
2. σ2 – неизвестна.
Критерий проверки гипотез представим в виде таблицы:
| H0 | Статистический критерий | H1 | Область принятия гипотезы H0 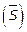
|
| a = a0 | 
| a ≠ a0 |  ; (-tα, tα) - двусторонняя критическая область ; (-tα, tα) - двусторонняя критическая область
|
| a = a1 > a0 |  ; (-∞, t2α) - правосторонняя критическая область ; (-∞, t2α) - правосторонняя критическая область
| ||
| a = a1 < a0 | 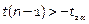 ; (-t2α,+∞) - левосторонняя критическая область ; (-t2α,+∞) - левосторонняя критическая область
|
Замечание: принятие основной гипотезы H0 не означает, что H0 является единственно подходящей, а только то, что H0 не противоречит выборочным данным, и нет оснований не принять H0.
Пример.
Фирма утверждает, что её изделие имеет срок службы 2900 часов. Для выборки из 50 изделий оказалось, что средний срок службы  часов. При исправленном среднем квадратическом отклонении S =700 часов проверить нулевую гипотезу H0 при 5%-м уровне значимости α =0,05.
часов. При исправленном среднем квадратическом отклонении S =700 часов проверить нулевую гипотезу H0 при 5%-м уровне значимости α =0,05.
Решение.
H0: a =2900
H1: a <2900
a0 =2900; n =50;  ч; S =700 ч; α =0,05.
ч; S =700 ч; α =0,05.
1) 
2) по таблице критических точек распределения Стьюдента найдём значение критической точки для односторонней (левосторонней) критической области при n-1 =50 и 2α =0,1: 

Ответ: Значение статистики, вычисленное по выборке, попадает в критическую область, поэтому гипотеза H0 не принимается.
§3. Гипотеза о равенстве дисперсий двух нормальных распределений.
Задача сравнения дисперсий возникает тогда, когда следует сравнить точность приборов, методов измерений и т.д. Предпочтительнее тот прибор или метод, который обеспечивает наименьшее рассеяние результатов измерений, т.е. наименьшую дисперсию. Пусть генеральные совокупности X и Y имеют нормальное распределение.
По независимым выборкам из этих совокупностей объёмом n1 и n2 вычислены исправленные выборочные дисперсии  и
и  . Задан уровень значимости α.
. Задан уровень значимости α.
Требуется проверить гипотезу


Статистический критерий проверки:  ,
,  .
.
Эта статистика имеет распределение Фишера со степенями свободы n1-1 и n2-1. Область принятия гипотезы определяется неравенством  .
.
Критическую точку  находят по таблице критических точек распределения Фишера по уровню значимости α и числам степеней свободы n1-1 и n2-1. Если проверяется та же нулевая гипотеза, но альтернативная гипотеза – другая.
находят по таблице критических точек распределения Фишера по уровню значимости α и числам степеней свободы n1-1 и n2-1. Если проверяется та же нулевая гипотеза, но альтернативная гипотеза – другая.


В этом случае область принятия гипотезы определяется неравенством 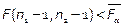 .
.
Критическая область будет двусторонней, но можно использовать только правостороннюю критическую область.
Точку  находят по уровню значимости
находят по уровню значимости  и заданным степеням свободы n1-1 и n2-1. Если гипотезу H0 принимают, то говорят, что различие исправленных выборочных дисперсий
и заданным степеням свободы n1-1 и n2-1. Если гипотезу H0 принимают, то говорят, что различие исправленных выборочных дисперсий  и
и  статистически не значимо и за оценку общей дисперсии принимают
статистически не значимо и за оценку общей дисперсии принимают  .
.
§4. Гипотеза о равенстве средних двух нормальных распределений.
Пусть имеются две генеральные совокупности X и Y, имеющие нормальное распределение и по выборкам объёма n1 и n2 рассчитали выборочные средние при заданном уровне значимости проверить нулевую гипотезу, состоящую в том, что математические ожидания рассматриваемых совокупностей равны. Критерии проверки гипотез представим в виде таблицы.
| Ho | Предположения | Статистика критерия | H1 | Область принятия гипотезы H0 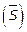
|
| ax = ay |  и и  - известны - известны
| 
| ax ≠ ay ax > ay ax < ay |  , ,  - двусторонняя критическая область - двусторонняя критическая область
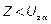 , ,  - правосторонняя критическая область - правосторонняя критическая область
 , ,  - левосторонняя критическая область - левосторонняя критическая область
|
 и и  - неизвестны, - неизвестны,

| 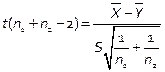 , ,
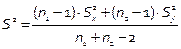 - общая оценка дисперсии - общая оценка дисперсии
| ax ≠ ay ax > ay ax < ay |  , ,  - двусторонняя критическая область - двусторонняя критическая область
 , ,  - правосторонняя критическая область - правосторонняя критическая область
 , , 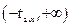 - левосторонняя критическая область - левосторонняя критическая область
|
Если H0 принимается, то говорят, что различие выборочных средних  и
и  статистически незначимо, и оценка общего математического ожидания такова:
статистически незначимо, и оценка общего математического ожидания такова:  .
.
§5. Гипотеза о вероятности появления некоторого события.
Проводится n испытаний Бернулли и считается относительная частота появления успеха. Требуется проверить гипотезу о вероятности успеха в единичном испытании.
Обозначим p0 – гипотетическое значение вероятности успеха. Если выборки – большие, т.е.  и
и  , то можно считать, что относительная частота успеха имеет значение p* с нормальным распределением со средним
, то можно считать, что относительная частота успеха имеет значение p* с нормальным распределением со средним 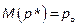 и средним квадратическим отклонением
и средним квадратическим отклонением  .
.
В качестве статистики критерия примем  .
.
H0: p = p0
H1: p = p1 ≠ p0
Область принятия Ho - двусторонняя критическая область,  .
.
H0: p = p0
H1: p = p1 > p0
Область принятия Ho - правосторонняя критическая область, 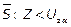 .
.
H0: p = p0
H1: p = p1 < p0
Область принятия Ho - левосторонняя критическая область,  .
.
Пример.
Торговец утверждает, что он получает заказы в среднем по крайней мере от 30% предполагаемых клиентов. Можно ли при 5%-м уровне значимости считать это утверждение неверным, если торговец получил заказы от 20 из 100 случайно отобранных потенциальных клиентов?
Решение.
H0: p0 =0,3
H1: p = p1 <0,3
n =100.  и
и  , поэтому для проверки H0 используем статистику
, поэтому для проверки H0 используем статистику  .
.
При  -
-  .
.
При α =0,05  , поэтому – U2α =-1,645.
, поэтому – U2α =-1,645.
Ответ: т.к. -2,18<-1,645, то H0 не принимается, значит, утверждение торговца не является правильным.
§6. Критерий согласия.
Не всегда есть основания высказать альтернативную гипотезу в явном виде. Часто в качестве альтернативной гипотезы имеется в виду невыполнение основной. В этом случае проверка основной гипотезы состоит в том, чтобы выяснить, согласуется ли высказанное в ней предположение с выборочными наблюдениями. Такие критерии называются критериями согласия.
Критерий согласия χ2 относительно закона распределения (критерий Пирсона).
1. H0: выборка извлечена из совокупности, имеющей распределение с функцией распределения F0(x), значения параметров которой известны.
Схема проверки гипотезы:
а) весь диапазон значений вариант выборки объёма n делится на интервалы одинаковой длины (xk-1, xk), i =1,2,…, k и подсчитывают число наблюдений mi в i -м интервале: 
б) предположив справедливость гипотезы H0 (т.е. предположение о законе распределения), подсчитывают вероятности  , i =1,2,…, k,
, i =1,2,…, k, 
в) подсчитывают ожидаемые частоты 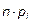 , i =1,2,…, k, при этом если для некоторых из интервалов ожидаемая частота
, i =1,2,…, k, при этом если для некоторых из интервалов ожидаемая частота 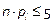 , то эти интервалы объединяют с соседними интервалами так, чтобы в итоге для каждого интервала ожидаемая частота была больше пяти; новое число интервалов обозначим
, то эти интервалы объединяют с соседними интервалами так, чтобы в итоге для каждого интервала ожидаемая частота была больше пяти; новое число интервалов обозначим 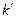
г) за меру расхождения выборочных наблюдений с гипотетическим распределением F0(x) принимается величина  (*), где
(*), где 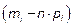 - это разность эмпирической и ожидаемой частот; эту разность возводят в квадрат, чтобы устранить возможность погашения положительных и отрицательных разностей; делением на
- это разность эмпирической и ожидаемой частот; эту разность возводят в квадрат, чтобы устранить возможность погашения положительных и отрицательных разностей; делением на 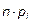 достигается уменьшение каждого слагаемого суммы, иначе сумма будет так велика, что приведёт к отклонению гипотезы H0 даже тогда, когда эта гипотеза верна
достигается уменьшение каждого слагаемого суммы, иначе сумма будет так велика, что приведёт к отклонению гипотезы H0 даже тогда, когда эта гипотеза верна
Если  , то распределение этой случайной величины (*) имеет распределение χ2 с
, то распределение этой случайной величины (*) имеет распределение χ2 с 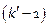 степенью свободы.
степенью свободы.
По вероятности α, где α – заданный уровень значимости, и числу степеней свободы 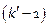 в таблице критических точек распределения χ2 находят
в таблице критических точек распределения χ2 находят  и сравнивают найденные значения с теми, которые посчитали по формуле (*). Если
и сравнивают найденные значения с теми, которые посчитали по формуле (*). Если  , то гипотеза H0 принимается.
, то гипотеза H0 принимается.
2. H0: выборка извлечена из совокупности, имеющей распределение с функцией распределения F0(x) с некоторыми, заранее не известными значениями параметра. Пусть таких параметров будет l. В этом случае выполняем точечные оценки этих параметров, а далее выполняем пункты а) - г) схемы пункта 1, но в этом случае величина (*) имеет распределение χ2 с  степенями свободы.
степенями свободы.
Пример.
Для определения средней заработной платы работников определённой отрасли было обследовано 100 человек. Результаты представлены в следующей таблице:
| Зарплата в долларах | Число человек |
| 190-192 | |
| 192-194 | |
| 194-196 | |
| 196-198 | |
| 198-200 | |
| 200-202 | |
| 202-204 | |
| 204-206 | |
| 206-208 |
Выяснить, можно ли на уровне значимости α =0,05 считать нормальным распределение средней заработной платы с параметрами a и σ?
Решение.
H0:  .
.
Прежде всего, находим оценки неизвестных параметров распределения:
 , где
, где  - середина i -го интервала
- середина i -го интервала  .
.




Введём стандартную нормальную величину  ,
,  . Далее будем считать, используя таблицу функции Лапласа:
. Далее будем считать, используя таблицу функции Лапласа:  , i =1,2,…,9.
, i =1,2,…,9.
| i | xi-1, xi | mi | Zi-1 | Zi | 
| 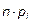
| 
| ||
| 190-192 | -2,928 | -2,275 | -0,4885-(-0,4982)=0,0097 | 0,97 | 5,08 | 0,1666 | |||
| 192-194 | -2,275 | -1,621 | -0,4474-(-0,4885)=0,0411 | 4,11 | |||||
| 194-196 | -1,621 | -0,967 | -0,3332-(-0,4474)=0,1142 | 11,42 | 0,5128 | ||||
| 196-198 | -0,967 | -0,314 | -0,1232-(-0,3332)=0,21 | 0,0476 | |||||
| 198-200 | -0,314 | 0,340 | 0,1331-(-0,1232)=0,2563 | 25,63 | 0,2192 | ||||
| 200-202 | 0,340 | 0,993 | 0,3396-0,1331=0,2065 | 20,65 | 0,1318 | ||||
| 202-204 | 0,993 | 1,647 | 0,4502-0,3396=0,1106 | 11,06 | 15,88 | 0,0009 | |||
| 204-206 | 1,647 | 2,301 | 0,4893-0,4502=0,0391 | 3,91 | |||||
| 206-208 | 2,301 | 2,954 | 0,4984-0,4893=0,0091 | 0,91 | |||||
| Итого | - | 0,9967 | - | 1,0789 |
χ2 =1,0789
При  -
-  .
.
1,0789<7,8, т.е.  , поэтому гипотеза H0 о нормальном распределении средней заработной платы принимается.
, поэтому гипотеза H0 о нормальном распределении средней заработной платы принимается.
Ответ: распределение средней заработной платы является нормальным.