Практическая работа № 2
Расчет доверительного интервала
Цель: оценить доверительные интервалы
Задание: решить задачи по варианту, оформить отчет.
Методические указания к выполнению практической работы:
Последовательность вычислений, следующая:
1. Исключить известные систематические ошибки (введением поправок).
2. Исключить " анормальные " результаты (промахи).
3. Вычислить среднеарифметическое исправленных результатов (эта величина и будет считаться наиболее достоверным результатом измерений).
4. Вычислить среднеквадратическую ошибку результатов измерений.
5. Оценить доверительные интервалы (погрешности) результатов измерений.
Среднее арифметическое. Среднеквадратическое отклонение. Среднее арифметическое выборки - выборочное среднее - лучшая оценка генерального среднего. Среднее из определений (замеров) обозначается как 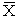 n:
n:
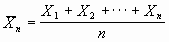 .
. 

Среднеквадратическое отклонение результатов измерения рассчитывается по формуле:
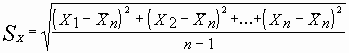
или

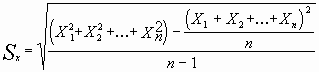 ,
,
где n - объем выборки (число замеров), Sx - среднеквадратическое отклонение, Х1, Х2,.....Хn- результаты замеров, 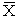 n - выборочное среднее.
n - выборочное среднее.
3. По таблице 1 для принятой 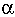 и n находят доверительные границы отклонения величины Sx (в долях Sx)
и n находят доверительные границы отклонения величины Sx (в долях Sx) 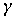
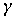 1 и
1 и 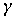 2.
2.
Таблица 1. Коэффициенты 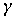 1 и
1 и 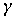 2 для оценки доверительных интервалов ошибок расчета среднеквадратического отклонения.
2 для оценки доверительных интервалов ошибок расчета среднеквадратического отклонения.
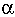 = 0.95 = 0.95
| 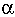 = 0.90 = 0.90
| |||
| n | 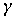 1 1
| 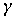 2 2
| 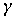 1 1
| 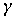 2 2
|
| 0.42 0.52 0.57 0.60 0.62 0.64 0.66 0.68 0.69 0.71 0.73 0.74 0.75 0.76 0.78 0.80 0.84 | 6.3 3.7 2.9 2.5 2.2 2.0 1.9 1.8 1.7 1.6 1.5 1.5 1.5 1.4 1.3 1.2 | 0.51 0.58 0.62 0.65 0.67 0.69 0.70 0.72 0.73 0.75 0.76 0.77 0.79 0.79 0.81 0.83 0.86 | 4.4 2.9 2.4 2.1 1.9 1.8 1.7 1.6 1.5 1.5 1.4 1.4 1.4 1.3 1.3 1.2 |
4. Находят доверительные границы отклонения Sx:
Sмин = SX 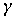 1, Sмакс= SX
1, Sмакс= SX 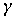 2,
2,
Полученные значения Sмин и Sмакс означают, что с вероятностью 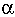 величина Sx лежит между ними. С учетом доверительных интервалов Sx далее рассчитываются доверительные интервалы погрешности измерения.
величина Sx лежит между ними. С учетом доверительных интервалов Sx далее рассчитываются доверительные интервалы погрешности измерения.
Оценка правильности результатов измерений (определений)
Доверительный интервал (Ах).
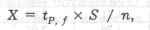
где tP, f — квантиль распределения Стьюдента при числе степеней свободы f = п - 1 и двухсторонней доверительной вероятности Р (значения tp, f см. в табл. 1.2).
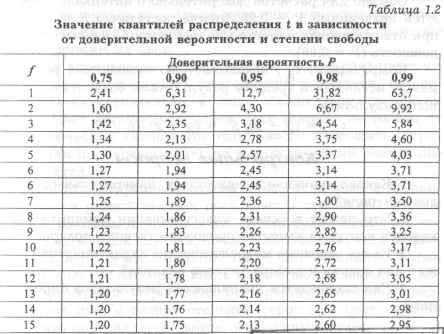 Обычно для расчетов доверительного интервала пользуются значениями Р = 0,95; иногда достаточно Р = 0,90, но при ответственных измерениях требуется более высокая надежность (Р = 0,99).
Обычно для расчетов доверительного интервала пользуются значениями Р = 0,95; иногда достаточно Р = 0,90, но при ответственных измерениях требуется более высокая надежность (Р = 0,99).
Коэффициент tp, fпоказывает, во сколько раз разность между истинным и средним результатами больше стандартного результата.

Ход работы:
Решить задачи по варианту.
| Вариант 1. Задача 1. Sx = 0.08, n = 9. Оценим границы доверительных интервалов. | Вариант 2. Задача 1. Sx = 0.07, n = 7. Оценим границы доверительных интервалов. |
| Задача 2. При замере химических результатов получили путем замеров на микрозонде 8 значений ХPlAn: 0.70,0.71, 0.68, 0.69, 0.72, 0.71, 0.67, 0.69. Необходимо определить среднее арифметическое и среднеквадратическую ошибку (S x) и доверительные интервалы для Sx. | Задача 2. При определении состава синтезированного в опыте бензола получили путем замеров на микрозонде 9 значений ХPlAn: 0.40,0.41, 0.38, 0.39, 0.42, 0.41, 0.37, 0.39, 0.40. Необходимо определить среднее арифметическое и среднеквадратическую ошибку (S x) и доверительные интервалы для Sx. |
| Задача 3. В результате определения содержания магния в сплаве получены следующие значения (в % масс): 5.88, 5.89, 5.98, 5.87, 5.90. Нужно рассчитать среднее и доверительный интервал. | Задача 3. В результате определения содержания железа в сплаве получены следующие значения (в % масс): 6.78, 6.79, 6.77, 6.85, 6.80. Нужно рассчитать среднее и доверительный интервал. |
Контрольные вопросы
1. Что называется систематической погрешностью?
2. Что называется случайной погрешностью?
3. Что называется грубой погрешностью?
4. Что называется доверительной вероятностью?
5. Приведите расчетную формулу при большом числе измерений полуширины доверительного интервала при заданном значении.
Пример:
В результате определения содержания алюминия в сплаве получены следующие значения (в % масс): 7.48, 7.49, 7.58, 7.47, 7.50. Нужно рассчитать среднее и доверительный интервал.
Решение:
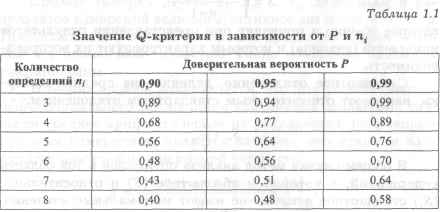
Сначала проверяем на промах крайние значения. Наибольшее значение - 7.58. По Q-критерию:
Q = (7.58 - 7.50) / (7.58 - 7.47) = 0.727. Оно больше табличного критического значения Qкритич(n = 5) = 0.64. Вывод - значение 7.58 является промахом, отбрасываем его. Убеждаемся, что остальные значения не являются промахами.
Рассчитываем среднее: 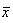 = (7.48 + 7.49 + 7.47 + 7.50) / 4 = 7.485
= (7.48 + 7.49 + 7.47 + 7.50) / 4 = 7.485
и дисперсию: V(x) = ((7.48 - 7.485)2 + (7.49 - 7.485)2+ (7.47 - 7.485)2 + (7.50- 7.485)2)/(4-1) = 0.000167.
Число степеней свободы нашей дисперсии на единицу меньше числа значений: f = 4 - 1 = 3.
Стандартное отклонение вычисляем, извлекая квадратный корень из дисперсии: S = 0.01291
Рассчитываем доверительный интервал, используя табличное значение критерия Стьюдента (t-критерия)
t(f = 3, p = 0.95) = 3.18, 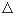 = 3.18 * 0.01291 / 2 = 0.205269.
= 3.18 * 0.01291 / 2 = 0.205269.
Округляем доверительный интервал до одной значащей цифры: 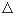 = 0.2, и до этого же знака округляем среднее:
= 0.2, и до этого же знака округляем среднее: 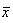 = 7.5
= 7.5
Ответ: 7.5 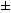 0.2
0.2