В работе рассмотрим только гипотезу о неравенстве средних значений.
Двухсторонняя область:
Нулевая гипотеза Но: mХ = mY
Конкурирующая гипотеза Н1: |mХ - mY| > 0.
Для оценки mХ и mY используем их наилучшие оценки 
и 
, а для оценки s2 используем исправленные выборочные дисперсии.
Так как генеральные совокупности X и Y имеют одинаковые дисперсии, то для оценки s2 целесообразно использовать результаты обоих выборок. Можно показать, что лучшей оценкой для s2 в данном случае является средняя взвешенная
= 
Если гипотеза Но справедлива, то случайная величина ( - ) подчиняется нормальному закону распределения с параметрами (0,s2(1/n1 + 1/n2)), т.к.
m( - )=m() – m()=0
s2( - )= s2 () + s2 ()=s2/n1 + s2/n2 =s2(1/ n1 + 1/n2)
Т.к. s2 неизвестна, то в качестве статистики для оценки дисперсии s2( - ) принимается несмещенная оценка 
=0,08*2.120=0,170
Статистика t = 
[( - )- М( - )]/ 
имеет t – распределение c число степеней свободы k = n1+ n2 -2=48.
Если гипотеза Но справедлива (средние равны), то статистику t можно записать в виде
t = ( - )/ 
= (0,688 – 0,707) / 0,170 = -0,113
По выбранной надежности g=1-a=0,95, по таблице распределения Стьюдента определить критическое значение 
, для которого
P (
> ) = a
=1,677
Т.к. 
<1,667, т.е. < , следовательно, с надежностью g=1-a=0,95 расхождение средних можно считать незначимым (случайным) и гипотеза о равенстве средних принимается.
Часть VI. Проверка гипотезы о нормальном распределении. Критерий 
.
Задача 1. Приближенная проверка гипотезы нормальности распределения с помощью асимметрии и эксцесса. Асимптотический подход.
Известны приближенные значения средних квадратических отклонений асимметрии А и эксцесса Е для случая нормального генерального распределения
s (А) = 
s (Е) = 
Используя известный результат для нормального распределения
Р (êХ-mï<l s) = 2Ф(l),
получаем
Р(ê А ï> l s(А) или ê Е ï> l s(E)) £ Р(ê А ï> l s(А) + P(ê Е ï> l s(E)) =
= 1 - 2Ф(l) + 1 - 2Ф(l) = 2(1 - 2Ф(l)) = 1- p = a
Отсюда Ф(l) = 0.5 – 0.25a
Тогда l = Ф-1 (0.5 – 0.25a) = Ф-1 (0.5 – 0.25*0,05) = Ф-1(0,4875)=2,24
Если произойдет хотя бы одно из событий êАï>ls(А) или êЕï>ls(E), то произойдет сумма этих событий с вероятностью, не превышающей a.
Критерий.
1. Назначается уровень значимости. Пусть a=0,05
2. По найденным ранее значениям А=−0,116 и Е 
−0,845 вычисляем s(А), s(Е) и l. s(А)=0,245, s(Е)=0,490, l=2,24; ls(А) = 0,549; ls(E) = 1,110.
3. Т.к. êАï<0,549 (|-0,116|<0,549), êЕï<1,10 (|-0,845|<1,110), то на уровне значимости a=0,05 гипотеза нормальности генеральной совокупности принимается.
Рассмотренный критерий можно рассматривать как предварительный, предшествующий более основательной проверке гипотезы по методу Пирсона ().
Задача 2. Проверка гипотезы о нормальном распределении по критерию .
Нулевая гипотеза Но: Генеральная совокупность имеет нормальное распределение. Т.к. параметры m и s неизвестны, то в качестве: 
0,531(исправленное С.К.О.) 
.
Зададим уровень значимости a =0,05
Выборочная статистика критерия 
вычисляется по формуле: 
; 
- абсолютная частота попадания в «i» интервал;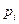 
- вероятность попадания Х (нормально распределенная случайная величина) в “i” интервал.
Правило принятия решения: Если 
, то на уровне значимости a нет основания отвергнуть гипотезу Но:
- это статистика с числом степеней свободы s = r – l - 1, где r- это число интервалов, а l – число неизвестных параметров (в нашем случае l=2), следовательно, в нашем случае s = r – 2 – 1 = r – 3 = 6 – 3 = 3.
Шаг 1: В качестве начальной таблицы возьмем таблицу группированной выборки Критерий использует тот факт, что случайная величина 
(i=1,2..k) имеет распределение близкое к нормальному закону N(0;1). Чтобы это утверждение было достаточно точным необходимо, чтобы для всех интервалов выполнялось условие 
. Если в некоторых интервалах это условие не выполняется, то их объединяем с соседними интервалами.
| № | Интервалы |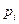
|
| n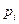
| 
|
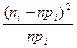
| [-1,2698; -0,5496) | 0,0681 | 6,81 | 0,005301 | ||
| [-0,5496; -0,18952) | 0,138 | 13,8 | 1,046377 | ||
| [-0,18952;0,170557) | 0,2382 | 23,82 | 1,603375 | ||
| [0,170557;0,530635) | 0,2611 | 26,11 | 0,370437 | ||
| [0,530635;0,890712) | 0,1829 | 18,29 | 0,401536 | ||
| [0,890712; 1,60868) | 0,1117 | 11,17 | 0,421567 | ||
| 
| 
| 
|
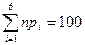
Шаг 2: Вычисляем теоретические вероятности:
· 
=0,5+Ф(-1,49)= 0,5-0,4319=0,0681
· 
=Ф(-0,82)-Ф(-1,49)= -0,2939-(-0,4319)=0,138
· 
=Ф(-0,14)-Ф(-0,82)=-0,0557-(-0,2939)=0,2382
· 
= Ф(0,54)-Ф(-0,14)=0,2054-(-0,0557)=0,2611
· 
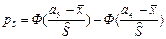= Ф(1,22)-Ф(0,54)=0,3883-0,2054=0,1829
· 
=0,5-Ф(1,22)=0,5-0,3883=0,1117
Получили, что 
=3,849, 
7,8
Следовательно,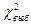 
< 
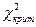(3,849 < 7,8), значит на уровне значимости a =0,05 нет основания отвергнуть гипотезу Но.
Заключение.