-0,730 0,06 0,07 [-0,5496;-0,18952)
| -0,370 0,1 0,17 [-0,18952;0,170557)
-0,009 0,3 0,47 [0,170557;0,530635)
|| 0,351 0,23 0,7 [0,530635;0,890712)
Nbsp; åni = 100 åpi* = 1 6. Статистический ряд: Zi -1,090 -0,730 -0,370 -0,009 0,351 0,711 1,071 1,431 Pi* 0,01 0,06 0,1 0,3 0,23 0,21 0,08 0,01 Определяем моду: - 0,09 7. Полигон частот: 8. Составим статистическую функцию распределения: x≤ -1,09 0,01 -1,09 < x ≤ -0,73 0,07 -0,73 < x ≤ -0,37 0,17 -0,37 < x ≤ -0,01 F*(x)= 0,47 -0,01 < x ≤ 0,35 0,7 0,35 < x ≤ 0,71 0,91 0,71 < x ≤ 1,07 0,99 1,07 < x ≤ 1,43 x> 1,43 F*(x) – приближенная функция распределения исследуемой генеральной совокупности. 9. Строим дополнительную таблицу: N Hi=Pi*/D 0,028 0,167 0,278 0,833 0,639 0,583 0,222 0,028 Строим гистограмму выборки: Часть III. Вычисление выборочных характеристик. 1. Линейное преобразование выборки. Введем новую случайную величину:. Пусть Мо= (k=4). № V № V № V № V № V -3,500 -0,401 0,327 1,028 2,056 -2,665 -0,328 0,358 1,029 2,120 -2,609 -0,322 0,381 1,062 2,122 -2,255 -0,208 0,394 1,097 2,167 -2,135 -0,179 0,436 1,110 2,191 -1,646 -0,161 0,471 1,153 2,228 -1,506 -0,115 0,495 1,297 2,333 -1,408 -0,104 0,594 1,421 2,338 -1,368 0,008 0,657 1,463 2,453 -1,263 0,014 0,677 1,490 2,453 -1,164 0,054 0,688 1,528 2,480 -0,956 0,069 0,752 1,568 2,531 -0,902 0,103 0,789 1,652 2,563 -0,854 0,136 0,817 1,829 2,592 -0,702 0,167 0,846 1,887 3,059 -0,634 0,197 0,859 1,959 3,365 -0,542 0,239 0,868 1,963 3,408 -0,487 0,256 0,887 1,994 3,413 -0,430 0,293 0,924 1,998 3,467 -0,415 0,314 1,023 2,029 4,500 Z -1,090 -0,730 -0,370 -0,009 0,351 0,711 1,071 1,431 Vi -3 -2 -1 P*i 0,03 0,04 0,1 0,3 0,23 0,21 0,08 0,01 2. Вычисление выборочного среднего. Вычисляем выборочное среднее по формуле: Вычисляем + и сравниваем с первоначальным вычислением по всей выборке. Они равны. 3. Вычисление выборочных дисперсий. Вычислим выборочные дисперсии: ; S2[V]= · Выборочная дисперсия генеральной совокупности Х: Сравниваем с числом. Они равны. · Исправленная выборочная дисперсия: · Центрированная выборочная дисперсия: – раньше была. 4. Вычисление выборочного С.К.О.: S(x)= Ŝ(x)= 5. Вычисление нормированных центральных выборочных моментов. Асимметрия A и эксцесс E эмпирического распределения вычисляются по следующим формулам: (;) Чтобы вычислить центральные эмпирические моменты 3-го и 4-го порядков, воспользуемся методом произведений. -1,090 -3 -3 -27 -0,730 -2 -12 -48 -0,370 -1 -10 -10 -0,009 -25 0,351 0,711 1,071 1,431 n=100 ∑ ∑ ∑ ∑ ∑ Контроль: ∑ ∑ ∑ ∑ ∑ +n=1450+4*386+6*238+4*68+100=4794 Совпадение сумм свидетельствуют о том, что вычисления произведены правильно. Найдем условные моменты 1го, 2го, 3го и 4го порядка: 3,86; 14,5 = Найдем центральные эмпирические моменты 3го и 4го порядка: -0,017 0,167 Следовательно: A = -0,116 E = -0,845 6. Занесем результаты в таблицу: Числовые характеристики По выборке По группированной выборке 0,243 0,243 0,282 0,282 0,279 0,279 0,281 0,281 0,25 0,25 Ŝ 0,531 0,531 0,530 0,530 − -0,116 − -0,845 Краткий анализ полученных результатов: Из таблицы нормально распределенных случайных чисел составлена выборка объема n=100. Заданы параметры нормального закона распределения m = 0,2, s = 0,5. По данным выборки найдены выборочные числовые характеристики эмпирического распределения =0,243, =0,279, S= =0,528, которые приблизительно равны параметрам нормального распределения. При этом характеристики, полученные по группированной выборке, с точностью до тысячных долей совпадают с данными, вычисленными по всей выборке, что позволяет предположить, что исследуемое распределение устойчиво к линейным преобразованиям случайной величины. Чтобы количественно оценить отличие эмпирического распределения от нормального, вводят специальные характеристики – асимметрию и эксцесс. Асимметрия задает степень асимметричности плотности вероятности относительно математического ожидания. Эксцесс задает степень пологости графика плотности. Для нормального распределения А=0 и Е=0. Т.к. A -0,116, то график отклонен влево от математического ожидания; при этом Е=-0,845, что говорит нам о том, что эмпирическое распределение имеет более низкую и «плоскую» вершину, чем нормальная кривая. Также можно сделать вывод о близости эмпирического распределения к нормальному. Глава IV. Построение доверительных интервалов. 1. Построение доверительного интервала для математического ожидания при известной дисперсии. Дано: · X N(m;s) нормальное распределение · s=0,5, n=100, =0,243 · Доверительная вероятность (надежность) задана: р= =1- =0,95 Построить доверительный интервал для математического ожидания: P{m (}= Решение: · Рассмотрим стандартную нормальную величину: =; zÎN(0;1). · Тогда, для нормально распределенной с.в. при Ф(z)= получим P{ }=2Ф()= =0,95 или Ф()=0,475. Отсюда по таблице значений функции Лапласа находим =1,96. · −0,098 0,098; 0,145 0,341. · Получили, что P{m (0,145; 0,341)}=0,95, где =0,098, то есть с надежностью =0,95 можно утверждать, что доверительный интервал (0,145; 0,341) покрывает неизвестное математическое ожидание m; точность оценки =0,098. 0,95 0,025 0,025 -0,098 0,098 Вопрос: Каким должен быть объем выборки n, чтобы? Ответ: Если, то имеет место неравенство < В ходе преобразований получаем. Объем выборки должен быть больше 100. 2. Построение доверительного интервала для математического ожидания при неизвестной дисперсии. Дано: · X N(m;s) нормальное распределение · Т.к. s неизвестная величина, то используем исправленную выборочную дисперсию Ŝ2=0,282 · n=100, =0,243 · Доверительная вероятность (надежность) задана: р= =1- =0,95 Построить доверительный интервал для математического ожидания: P{m (}= Решение: · Рассмотрим случайную величину - распределение Стьюдента, число степеней свободы k = 100-1=99. Используем t-распределенную случайную величину: ·. По таблице распределения Стьюдента =t(n-1,γ)=t(99;0,95)=1,984 · · -0,056 0,056 · 0,187 0,300 Получили, что P{m (0,187;0,300)}=0,95, где =0,056, то есть, пользуясь распределением Стьюдента, мы нашли доверительный интервал (0,187;0,300), покрывающий неизвестное математическое ожидание с надежностью 0,95. 0,05 -1,984 1,984 3. Построение доверительного интервала для дисперсии при условии, что математическое ожидание известно. Дано: · X N(m;s) нормальное распределение. · µ=0,2, n=100, =0,281. · Доверительная вероятность: =1- =0,95. Найти доверительный интервал для дисперсии: P{ (}= Решение: Рассмотрим с.в.: (n степеней свободы), где S20 – центрированная выборочная дисперсия. По таблице распределения Пирсона (распределение) найдем: = =74,22 = =129,6 0,217 0,378 P{ (}= P{ (}= Получили P{ (}= То есть, пользуясь таблицей распределения Пирсона, мы нашли доверительный интервал (, покрывающий неизвестную дисперсию с надежностью 0,95. 4. Построение доверительного интервала для дисперсии при неизвестном математическом ожидании. Дано: · X N(m;s) нормальное распределение. · n=100, Ŝ2=0,282. · Доверительная вероятность: =1- =0,95. Найти доверительный интервал для дисперсии: P{ (}= Решение: Рассмотрим с.в.: с (n-1) степенями свободы; k= n-1 = 99. По таблице распределения Пирсона найдем: = =73,36 = =128,42 0,217 0,380 P{ (}= P{ (}= Получили P{ (}= то есть, пользуясь таблицей распределения Пирсона, мы нашли доверительный интервал (, покрывающий неизвестную дисперсию с надежностью 0,95. Часть V. Проверка статистических гипотез. Критерий значимости. Задача 1. Проверка гипотезы о значении математического ожидания m (генеральной средней) при известном s. Дано: · X N(m;s) нормальное распределение · n=100, =0,243 · =0,5, -уровень значимости, =0,05 -нулевая гипотеза: - альтернативная гипотеза: Нам нужно выбрать одну из односторонних гипотез, а именно: если то имеем правостороннюю гипотезу:. Если то имеем левостороннюю гипотезу:. Т.к. =0,243, =0,2 и 0,243 > 0,2, то имеем правостороннюю гипотезу:. Решение: Статистика критерия: - стандартно распределенная случайная величина. Вычислим выборочное значение этой величины, используя условие задачи: Строим критическую область: Для двусторонней гипотезы: Правило принятия решения: Если Ф(zкрит) = (1 - a)/2, то нет основания отвергнуть гипотезу на уровне значимости a. А если то мы попадаем в критическую область и гипотезу на уровне значимости a отвергаем. Итак, Ф(zкрит) = (1 - a)/2=0,475, следовательно, zкрит=1,96. 0,868<1,96 нет основания отвергать гипотезу: на уровне значимости a=0,05. Для правосторонней гипотезы:: Правило принятия решения: Если Ф(zкрит) = (1 - 2a)/2, то нет основания отвергнуть гипотезу на уровне значимости a. А если то мы попадаем в критическую область и гипотезу на уровне значимости a отвергаем. Итак, Ф(zкрит) = (1 - 2a)/2=0,45, следовательно zкрит=1,65. 0,868<1,65 нет основания отвергнуть гипотезу: на уровне значимости a=0,05. Задача 2. Проверка гипотезы о значении математического ожидания (генеральной средней) при неизвестном s. Дано: · X N(m;s) нормальное распределение · n=100; =0,243; Ŝ2=0,282 · -уровень значимости, =0,05 -нулевая гипотеза: Альтернативные гипотезы: : (двусторонняя) : (правосторонняя) Решение: Статистика критерия: - распределение Стьюдента, число степеней свободы k = n-1=99. Вычисляем выборочное значение на основании исходных данных: Строим критическую область: Для двусторонней гипотезы: - границы критической области. Правило принятия решения: Если то нет основания отклонить гипотезу на уровне значимости a. А если то мы попадаем в критическую область и гипотезу на уровне значимости a отвергаем. Итак, =t(99, 0,05)=1,984 1,534<1,984 нет основания отвергнуть гипотезу: на уровне значимости a=0,05. Для правосторонней гипотезы: - граница правосторонней критической области. Правило принятия решения: Если то нет основания отклонить гипотезу на уровне значимости a. А если то мы попадаем в критическую область и гипотезу на уровне значимости a отвергаем. Итак, для правосторонней критической области =t(99, 0,05)=1,660 0,534<1,660 нет основания отвергнуть гипотезу: на уровне значимости a=0,05. Задача 3. Проверка гипотезы о числовом значении дисперсии генеральной совокупности при известном значении математического ожидания генеральной совокупности. Дано: · X N(m;s) нормальное распределение · n=100, D= = 0,25, =0,281 · -уровень значимости, =0,05 -нулевая гипотеза: Альтернативные гипотезы: : (двусторонняя) H1(2): (правосторонняя, т.к.) Решение: Статистика критерия: - распределение с числом степеней свободы n=100 Вычисляем выборочное значение Строим критические области: Для двусторонней гипотезы:: Правило принятия решения: Если, то нет основания отклонить гипотезу на уровне значимости a. А если,, то гипотезу отвергаем на уровне значимости a. Т.к = 112,266, (74,22; 129,6), следовательно, нет основания отклонить гипотезу на уровне значимости a. Для правосторонней гипотезы:: Правило принятия решения: Если, то нет основания отклонить гипотезу на уровне значимости a. А если,, то гипотезу отвергаем на уровне значимости a. Т.к. =112,266, =124,42, то, следовательно, нет основания отклонить гипотезу на уровне значимости a. Задача 4. Проверка гипотезы о числовом значении дисперсии генеральной совокупности при неизвестном значении математического ожидания Дано: · X N(m;s) нормальное распределение · n=100, D= =0,25, Ŝ2=0,282 · -уровень значимости, =0,05 -нулевая гипотеза: Альтернативные гипотезы: : (двусторонняя) : (правосторонняя, так как) Решение: Статистика критерия: - распределение с числом степеней свободы n=99. Вычисляем выборочное значение Строим критические области: Для двусторонней гипотезы:: Правило принятия решения: Если, то нет основания отклонить гипотезу на уровне значимости a. А если,, то гипотезу отвергаем на уровне значимости a. Т.к =111,512, (73,36; 128,42), следовательно, нет основания отклонить гипотезу на уровне значимости a. Для правосторонней гипотезы:: Правило принятия решения: Если, то нет основания отклонить гипотезу на уровне значимости a. А если,, то гипотезу отвергаем на уровне значимости a. Т.к. =111,512, =123,31, то, следовательно, нет основания отклонить гипотезу на уровне значимости a. Задача 5. Проверка гипотезы о сравнении двух средних нормальных совокупностей, дисперсии которых неизвестны и одинаковы (малые независимые выборки). Дано: Из исходной генеральной совокупности объемом 100 образуем две выборки X и Y объемами 25, пользуясь равномерным выбором четных и нечетных номеров исходной совокупности. № X Y -2,255 -2,135 -1,506 -1,408 -1,368 -1,164 -0,854 -0,902 -0,634 -0,702 -0,542 -0,487 -0,179 -0,104 0,008 0,014 0,054 0,069 0,293 0,256 0,358 0,394 0,471 0,436 0,657 0,677 0,846 0,859 0,868 0,887 1,028 1,023 1,153 1,110 1,421 1,463 1,568 1,528 1,994 1,998 2,120 2,122 2,338 2,333 2,531 2,592 3,365 3,408 3,467 3,413 Так как нет основания считать дисперсии каждой из выборок одинаковыми, то прежде, чем сравнивать их средние, необходимо по критерию Фишера - Снедекора проверить гипотезу о равенстве дисперсий.
|
|
|
|
|
|
I) Задача о сравнении двух дисперсий нормальных совокупностей.
По независимым выборкам Х и Y, объемы 25 (n1=n2), находим исправленные выборочные дисперсии 
и 
, где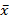 
- средняя выборочная совокупности Х, 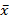=0,688
, где 
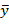- средняя выборочная совокупности Y, 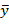=0,707
Ставится задача сравнить эти дисперсии (гипотеза об их равенстве) при некотором уровне значимости a.
Односторонняя область:
Нулевая гипотеза Но: D(X) = D(Y)
Конкурирующая гипотеза Н1: D(X) > D(Y)
Решение:
Для того, чтобы при заданном уровне значимости a проверить нулевую гипотезу, надо вычислить наблюдаемое значение критерия Fнаб.= 
и по таблице критических точек распределения Фишера-Снедекора по заданному уровню значимости a=0,05 с числом степеней свободы k1 = n1–1=24, k2 = n2–1=24 (где k1 – число степеней свободы большей исправленной дисперсии) найти по таблице F – распределения критическую точку Fкрит(a, k1, k2). Если выполняется неравенство Fнаб < Fкрит, то нет основания отвергнуть нулевую гипотезу, а если выполняется неравенство Fнаб > Fкрит, то нулевую гипотезу отвергают.
Fкрит(a, k1, k2)= Fкрит(0,05; 24, 24)=1,98
1,034239<1,98 
Fнаб<Fкрит нет основания отвергнуть нулевую гипотезу.
Двухсторонняя область:
Нулевая гипотеза Но: D(X) = D(Y)
Конкурирующая гипотеза Н1: D(X) ¹ D(Y)
Решение.
Находим из таблицы Фишера-Снедекора критическую точку Fкрит(a/2,k1,k2) по заданному уровню значимости a/2=0,025 и числу степеней свободы k1=n1–1=24, k2 =n2–1=24 (где k1 – число степеней свободы большей исправленной дисперсии). Если выполняется неравенство Fнаб < Fкрит, то нет основания отвергнуть нулевую гипотезу, а если выполняется неравенство Fнаб > Fкрит, то нулевую гипотезу отвергают.
Fкрит(a, k1, k2)= Fкрит(0,025; 24, 24)=2,27.
1,034239<2,27 Fнаб<Fкрит нет основания отвергнуть нулевую гипотезу.