При сопоставлении значений функций 
и 
для случайной величины x, распределённой нормально, при одном и том же значении аргумента, возникают ошибки 
. Эти ошибкой могут быть обусловлены либо ошибками определения величин M { x } и s2{ x }, либо тем, что закон распределения случайной величины отличен от закона Гаусса. Идея сравнения эмпирического распределения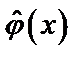 
с идеальным нормальным распределением 
, определённым величинами M { x } = 
и s 2{ x } = S 2{ x }, лежит в основе доказательства гипотезы о том, что случайная переменная подчиняется нормальному закону распределения.
Для проверки гипотезы о согласованности эмпирического выборочного распределения с гипотетическим нормальным распределением применяется статистика, которая приближённо распределена по c 2-закону Пирсона
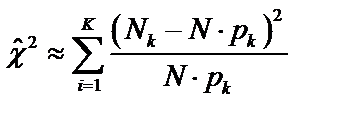
с числом степеней свободы f = K – l – 1, где K – число интервалов ряда распределения, определённое по (9), l – число параметров гипотетического распределения, которые надо определить по данным выборки (для нормального распределения l = 2). Здесь Nk – число элементов выборки, попавшее в k -ый интервал, а pk – вероятность попадания случайной величины x в k -ый интервал при условии, что x распределена нормально.
Для проверки нуль-гипотезы о соответствии выборочного распределения нормальному закону Гаусса вычисляют эмпирическое значение статистики по (15) и сравнивают его с критическим c 2КР{ q; f }, которое выбирают из таблиц c 2-распределения для числа степеней свободы f и выбранного уровня значимости q. Если выполняется условие
то гипотеза принимается, эмпирическое распределение считается нормальным.
Критерием Пирсона рекомендуется пользоваться при N > 50. При меньших объёмах выборки можно воспользоваться критерием согласия:
где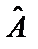 
, 
– соответственно асимметрия и эксцесс эмпирического распределения, а DA и DE – дисперсии данных величин. Величины 
, 
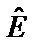, DA и DE определяются по выражениям
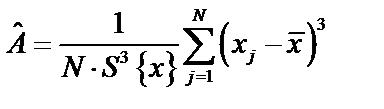
При выполнении условий (17) гипотеза о соответствии выборочного распределения нормальному закону Гаусса принимается.
2. ПРАКТИЧЕСКИЕ УПРАЖНЕНИЯ
Перед началом практических занятий по темам, затронутым в первой части методических указаний, каждому студенту (подгруппе студентов) выдаётся текстовый файл с разделителями, форма которого показана в таблице 1.
Таблица 1 - Форма файла исходных данных
| A | B | C | D | E | |
| 
| 
| 
| ||
| 
| 
| 
| ||
| 
| 
| 
| ||
| … | … | … | … | … | |
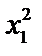
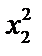
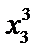
| j |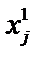 
| 
| 
| 
| |
| … | … | … | … | … | |
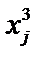
| N | 
| 
| 
| 
|
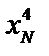
Файл представляет собой таблицу без заголовков. В первом столбце таблицы расположены номера опытов j = 1.. N. В остальных столбцах содержатся элементы выборочных статистических совокупностей четырёх случайных величин, подчиняющихся различным видам распределения. Все вычисления на практических занятиях производятся только для величины x 1. Определение расчётных параметров для остальных случайных величин производится путём копирования с заменой элементов 
(s = 2.. 4) в ячейки элементов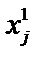 
.
Задание на практические занятия заключаются в следующем:
1. Выполнить точечную оценку параметров распределения случайной величины:
1) Определить среднее по выборке значение случайной величины 
при помощи функции СРЗНАЧ(
.. 
).
2) Определить значение выборочной дисперсии S 2{ x } при помощи функции ДИСП.В(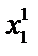
.. 
).
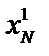3) Построить график случайной величины xj, 
.
4) При помощи функции определить значения относительных частот ν 1, ν 2, ν 3 попадания случайной величины x в интервалы M { x }± S { x }, (M { x }±2 S { x }, M { x }±3 S { x } соответственно. Для этого рекомендуется воспользоваться функцией ЧАСТОТА(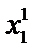
.. 
; С), показывающей количество элементов в массиве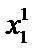 
.. 
, меньших указанной величины С.
5) Определить границы, симметричные относительно 
, доверительных интервалов наблюдения случайной величины x 1, распределенной нормально, для вероятностей P 1 = 0,68; P 2 =0, 95; P 3 = 0,99. При расчёте воспользоваться функцией НОРМОБР(P; 
, S { x }), возвращающей такое значение нормальной случайной величины X, описываемой параметрами 
и S { x }, что вероятность наблюдения x < X равна P.
6) выполнить сравнительный анализ величин, рассчитанных в п. 4) и 5).
2. Выполнить проверку гипотезы о соответствии распределения случайной величины x нормальному закону распределения по критериям согласия:
1) Рассчитать значение асимметрии 
распределения случайной величины x, воспользовавшись функцией СКОС(
.. 
).
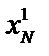2) Рассчитать значение эксцесса 
распределения случайной величины x, воспользовавшись функцией ЭКСЦЕСС(
.. 
).
3) Вычислить значения дисперсий рассеяния величин 
и 
по выражениям (20,21).
4) Сделать вывод о принятии или отклонении гипотезы о соответствии распределения случайной величины x нормальному закону.
3. Построить гистограмму случайной величины x 1:
1) Определить x min и x max (функции МИН(
.. 
) и МАКС(
.. 
)).
2) Определить количество К интервалов гистограммы по выражению (9). Для этого могут понадобиться функции ОКРУГВВЕРХ() и LOG10() приложения Microsoft Excel.
3) Определить границы интервалов гистограммы.
4) Подсчитать частоты Nk попадания случайной величины x в рассчитанные интервалы, воспользовавшись функцией ЧАСТОТА в матричном виде.
5) Построить график гистограммы по результатам работы функции ЧАСТОТА.
4. Выполнить проверку гипотезы о соответствии распределения случайной величины x нормальному закону распределения по c2-критерию:
1) Определить вероятности pk попадания случайной величины x 1 в k -ые интервалы гистограммы, воспользовавшись выражением (7) и функцией НОРМРАСП.
2) Рассчитать фактическое значение c2-критерия по выражению (15).
3) Определить критическое значение c2КР для вероятности p = 0,9. Для этоговоспользоваться функцией ХИ2ОБР[P2]).
4) сделать вывод о принятии или отклонении гипотезы о соответствии распределения случайной величины x нормальному закону.
5. Выполнить интервальное оценивание параметров генеральной совокупности случайной величины x при известных выборочных параметрах. Для определения квантилей распределения Стьюдента и Фишера воспользоваться функциями СТЬЮДРАСПОБР() и FРАСПОБР().
6. Выполнить пп. 1-5 для других случайных величин, имеющихся в файле исходных данных. Сделать выводы по результатам анализа.
ЛИТЕРАТУРНЫЕ ИСТОЧНИКИ
1. Лукьянов С.И. Основы инженерного эксперимента [Текст]: учеб.пособ. / МГТУ. - Магнитогорск, 2006. - 94с.: ил.
2. Фихтенгольц Г.М. Основы математического анализа [Электронный ресурс]: Учебник. Часть 1. 9-е изд.,стер. — СПб.: Издательство «Лань», 2008. — 448 с.: ил. (Учебники для вузов. Специальная литература). Режим доступа: https://e.lanbook.com/books/element.php?pl1_cid=25&pl1_id=410. ISBN 978-5-9511-0010-8 (Общий) ISBN 978-5-8114-0190-1 (Ч. 1).
3. Мойсюк Б.Н. / Основы теории планирования эксперимента: Учебное пособие // М.: Издательство МЭИ, 2005. – 464 с.
[P1]В бумажной версии здесь опечатка
[P2]В бумажной версии здесь опечатка