Тема. Решение задач по планам с горизонталями: определение координат точек земной поверхности, их высот; определение крутизны ската и уклона линии.
Цель: научиться решать задачи по планам с горизонталями:
- определение координат точек земной поверхности;
- определение отметок высот точек;
- определение крутизны ската и уклона линии.
Принадлежности: калькулятор, чертёжные инструменты, топографические планы и карты, образцы работ.
Литература: Киселёв М.И., Михелёв Д.Ш. «Геодезия» §§3.5 - 3.10 (стр.30 – 41), Родионов В.И.«Геодезия» §12 (стр.35-40);
Родионов В.И., Волков В.Н. «Задачник по геодезии» стр. 18-25.
Последовательность выполнения работы:
1. Определить прямоугольные координаты точки, заданной на топографической учебной карте (карту выдаёт преподаватель).
Масштаб карты 1: 50000. Квадрат координатной сетки, в котором расположена определяемая точка, отмечен с северной и восточной стороны рамки карты «галочками».
Смотреть пример на странице 8.
2. Ознакомиться с топографическим планом местности (план выдаёт преподаватель) и определить:
2.1. высоту сечения рельефа hсеч;
2.2. отметки высот точек А (НА), В (НВ), С (НС), заданных на плане.
Смотреть пример на странице 9.
3. Определить уклоны отрезков линии 1-2 и линии С-Д, заданных на топографическом плане масштаба 1: 25000.
Отрезки линий на земной поверхности обычно имеют какой-то наклон, отчего начало и конец отрезка находятся на разных высотах:
- разность этих высот – превышение;
- проекция отрезка на горизонтальную плоскость – его горизонтальное проложение.
Уклоном i линии называется отношение превышения h к горизонтальному проложению dм: i = h / dм.:
где: dм - горизонтальное проложение линии на местности в м;
|
|
h = H2 - H1 – превышение конца линии над её началом в м;
H2 и H1 – отметки высот концов отрезка линии.
На топографическом плане можно определить уклон любой линии, для этого надо найти отметки концов отрезка линии по отметкам горизонталей, а следовательно, и превышение. Горизонтальное проложение отрезка линии на местности можно определить с плана по масштабу.
Если концы отрезка линии лежат на смежных горизонталях, то превышение h будет равно высоте сечения рельефа hсеч.
По знаку уклоны могут быть положительными и отрицательными и выражаются в тысячных долях (‰).
4. Построить график заложений по углам наклона для топографического плана масштаба 1: 25000.
По уклону линии можно определить угол её наклона,
т. к. i = tg ν = h / dм .
По углу наклона ν определяется крутизна ската рельефа.
За направление ската принимают линию наибольшей крутизны, по которой свободно стекает вода.
При пользовании планом или картой углы наклона определяют с помощью графика заложений.
Последовательность построения графика:
4.1. из пункта 2 выписываем высоту сечения рельефа hсеч.;
4.2. принимаем h = hсеч.;
4.3. определяем длину отрезка линии dпл. на плане для различных углов её наклона ν не более 20º по формуле. dпл. = hсеч. / (М·tg ν ),
где:
dпл. – заложение линии на плане между двумя смежными горизонталями в мм;
ν – угол наклона в градусах;
hсеч. - высота сечения рельефа в м;
М – знаменатель масштаба плана (для масштаба 1: 25000, - на 1 мм длины отрезка линии на плане приходится 25 м этой линии на местности, значит М = 25 м/мм).
4.4. все вычисления заносим в таблицу
|
|
| Угол наклона ν | 1º | 2º | 3º | 4º | 5º | 10º | 15º | 20º |
| Заложения d, мм |
Построение:
- по горизонтальной оси графика откладываются углы наклона,
- по вертикальной оси – соответствующие этим углам заложения d (мм), выраженные в масштабе плана (карты).
5. Построить график заложений по уклонам для топографического плана масштаба 1: 25000, используя формулу: dпл. = hсеч.·10³ / (М ∙ i),
где i – уклон линии в «в тысячных», принимать от 10‰ до 100‰.
Построение выполнить аналогично построению графика заложения по углам наклона.
Примеры графиков заложений:
График заложенияГрафик заложения
по углам наклона по уклонам
6. Определить угол наклона и уклон отрезка линии СД, указанного на плане, расположенного между смежными горизонталями, пользуясь графиками заложений.
Содержание отчёта:
- тема и цель занятия;
- определение прямоугольных координат точки по учебной карте;
- определение отметок высот точек местности;
- построение графиков заложений;
- определение угла наклона и уклона отрезка линии СД;
- вывод.
Определения:
Расстояние между соседними горизонталями в плане (горизонтальное проложение) называется заложением.
Минимальным в данном месте является заложение, перпендикулярное к горизонталям, - заложение ската.
Контрольные вопросы
1. Как строится прямоугольная система координат в проекции Гаусса – Крюгера?
2. Что называется рельефом местности, и каковы его основные формы?
3. По каким признакам можно отличить возвышенность от впадины на топографических картах и планах?
|
|
4. Что называется линией ската?
5. Дайте определение уклона линии местности.
6. Назовите единицы измерения уклонов линии местности.
Примеры решения задач.
Пример № 1
Определить прямоугольные координаты точки Р, заданной на топографической карте М 1: 10000 (1см – 100м)
Рисунок показывающий расположение точи Р в квадрате километровой сетки:
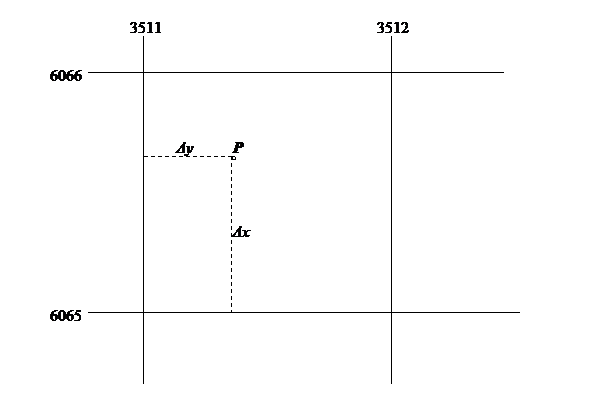Решение:
1. Заметив в каком квадрате километровой (координатной) сетки расположена определяемая точка Р, читают на выходахкилометровых линий за рамкой карты значения координат: Xю – для линии, ограничивающей квадрат с юга, и Yз – для линии, ограничивающей его с запада. В данном примере:
Xю = 6065км = 6065000м;
Yз = 3511км = 3511000м.
2. Из точки Р опускаем перпендикуляры на южную и западную стороны квадрата километровой сетки и измеряем их длину, т.е. определяем приращения координат согласно масштабу карты:
Δx = (6,5см) · (100м) = 650м;
Δy = (3,7см) · (100м) = 370м.
3. Сложив соответствующие координаты и их приращения, выраженные в метрах, находим координаты точки Р:
XР = Xю + Δx = 6065000 + 650 = 6065650м;
YР = Yз + Δy = 3511000 + 370 = 3511370м.
Пример № 2
Определить отметки высот точек А и В, отмеченных на топографическом плане.
 |
Рис. 1 План в горизонталях
Решение:
- Определяем высоты сечения рельефа плана:
hсеч. = (Н120 – Н115) / n = (120 – 115) / 5 = 1м
- Точка А лежит на горизонтали с отметкой Н117 = 117м. Высота точки, лежащей на горизонтали, равна высоте этой горизонтали,
значить НА = Н117 = 117м. - Высота точки В, расположенной между двумя горизонталями, определяется по формуле:
НВ = НМ + hсеч.·(b/a);
где НМ – высота младшей горизонтали равная НМ = 119м;
отрезки a и b - заложение ската и расстояние от точки В до младшей горизонтали, измеренное на плане линейкой в миллиметрах, равные a = 21мм; b = 10мм.
Вычисляем:
НВ = НМ + hсеч.·(b/a) = 119 + 1·(10/21) = 119,48м