Очень важным случаем движения в центрально-симметричном поле является движение в кулоновом поле

( - положительная постоянная). Мы будем рассматривать сначала кулоново притяжение, соответственно чему будем писать
- положительная постоянная). Мы будем рассматривать сначала кулоново притяжение, соответственно чему будем писать  . Из общих соображений заранее очевидно, что спектр отрицательных собственных значений энергии будет дискретным (с бесконечным числом уровней), а спектр положительных энергий – непрерывным.
. Из общих соображений заранее очевидно, что спектр отрицательных собственных значений энергии будет дискретным (с бесконечным числом уровней), а спектр положительных энергий – непрерывным.
Уравнение (1,8) для радиальных функций имеет вид
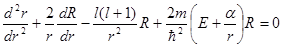 (3,1)
(3,1)
Если речь идет об относительном движении двух притягивающихся частиц, то под  надо подразумевать их приведенную массу.
надо подразумевать их приведенную массу.
В вычислениях, связанных с кулоновским полем, удобно пользоваться вместо обычных особыми единицами для измерения всех величин, которые мы будем называть кулоновскими единицами. Именно, в качестве единиц измерения массы, длины и времени выберем соответственно

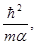

Все остальные единицы выводятся отсюда; так, единицей энергии будет
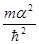 .
.
Далее будем пользоваться этими единицами.
Уравнение (3,1) в новых единицах принимает вид
 (3,2)
(3,2)
Дискретный спектр.
Введем вместо параметра  и переменной
и переменной  новые величины:
новые величины:

 (3,3)
(3,3)
При отрицательных энергиях  есть вещественное положительное число. Уравнение (3,2) после подстановки (3,3) приобретает вид
есть вещественное положительное число. Уравнение (3,2) после подстановки (3,3) приобретает вид
 (3,4)
(3,4)
(штрихи обозначают дифференцирование по  ).
).
При малых  решение, удовлетворяющее необходимым условиям конечности, пропорционально
решение, удовлетворяющее необходимым условиям конечности, пропорционально  (см. (1,15)). Для выяснения асимптотического поведения
(см. (1,15)). Для выяснения асимптотического поведения  при больших
при больших 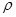 опускаем в (3,4) члены с
опускаем в (3,4) члены с  и
и  и получаем уравнение
и получаем уравнение

откуда  . Интересующее нас исчезающее на бесконечности решение, следовательно, при больших
. Интересующее нас исчезающее на бесконечности решение, следовательно, при больших  ведет себя, как
ведет себя, как  .
.
|
|
Виду этого естественно сделать подстановку
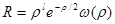 , (3,5)
, (3,5)
после чего уравнение (3,4) принимает вид
 (3,6)
(3,6)
Решение этого уравнения должно расходиться на бесконечности быстрее конечной степени 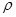 , а при
, а при  =0 должно быть конечным. Удовлетворяющее последнему условию решение есть вырожденная гипергеометрическая функция
=0 должно быть конечным. Удовлетворяющее последнему условию решение есть вырожденная гипергеометрическая функция

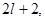
 (3,7)
(3,7)
Решение, удовлетворяющее условию на бесконечности, получится лишь при целых отрицательных (или равных нулю) значениях  , когда функция (3,7) сводится к полиному степени
, когда функция (3,7) сводится к полиному степени  . В противном случае она расходится на бесконечности, как
. В противном случае она расходится на бесконечности, как 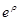 .
.
Таким образом, мы приходим к выводу, что число  должно быть целым положительным, причем при данном
должно быть целым положительным, причем при данном  должно быть
должно быть
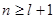 (3,8)
(3,8)
Вспоминая определение (3,3) параметра  , находим
, находим
 (3,9)
(3,9)
Этим решается задача об определении уровнем энергии дискретного спектра в кулоновском поле. Мы видим, что имеется бесконечное множество уровней между нормальным уровнем  и нулем. Интервалы между каждыми двумя последовательными уровнями уменьшаются с увеличением
и нулем. Интервалы между каждыми двумя последовательными уровнями уменьшаются с увеличением  ; уровни сгущаются по мере приближения к значению
; уровни сгущаются по мере приближения к значению 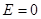 , при котором дискретный спектр смыкается с непрерывным. В обычных единицах формула (3,9) имеет следующий вид:
, при котором дискретный спектр смыкается с непрерывным. В обычных единицах формула (3,9) имеет следующий вид:
 (3,10)
(3,10)
Целое число  называется главным квантовым числом. Радиальное же квантовое число, определенное в п.1, равно
называется главным квантовым числом. Радиальное же квантовое число, определенное в п.1, равно
 .
.
При заданном значении главного квантового числа число  может принимать значения
может принимать значения
 (3,11)
(3,11)
всего  различных значений. В выражение (3,9) для энергии входит только число
различных значений. В выражение (3,9) для энергии входит только число  . Поэтому все состояния с различными
. Поэтому все состояния с различными  , но одинаковыми
, но одинаковыми  обладают одинаковой энергией. Таким образом, каждое собственное значение оказывается вырожденным не только по магнитному квантовому числу
обладают одинаковой энергией. Таким образом, каждое собственное значение оказывается вырожденным не только по магнитному квантовому числу  (как при всяком движении в центрально-симметричном поле), но и по числу
(как при всяком движении в центрально-симметричном поле), но и по числу  . Это последнее вырождение (о нем говорят, как о случайном или кулоновом) специфично именно для кулонового поля. Каждому данному значению
. Это последнее вырождение (о нем говорят, как о случайном или кулоновом) специфично именно для кулонового поля. Каждому данному значению  соответствует
соответствует  различных значений
различных значений  ; поэтому кратность вырождения
; поэтому кратность вырождения  - го уровня энергии равна
- го уровня энергии равна
|
|
 (3,12)
(3,12)
Волновые функции стационарных состояний определяются формулами (3,5), (3,7). Вырожденная гипергеометрическая функция с целыми значениями обоих параметров совпадает, с точностью до множителя, с так называемыми обобщенными полиномами Лагерра. Поэтому
 .
.
Радиальные функции должны быть нормированы условием
 .
.
Их окончательный вид следующий:
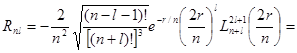
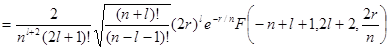 (3,13)
(3,13)
Вблизи начала координат  имеет вид
имеет вид
 (3,14)
(3,14)
На больших расстояниях
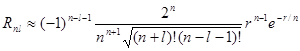 . (3,15)
. (3,15)
Волновая функция  нормального состояния затухает экспоненциально на расстояниях порядка
нормального состояния затухает экспоненциально на расстояниях порядка 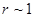 , т.е. в обычных единицах,
, т.е. в обычных единицах,  .
.
Средние значения различных степеней  вычисляются по формуле
вычисляются по формуле
 .
.
Приведем несколько первых величин  (с положительными и отрицательными
(с положительными и отрицательными  ):
):
 ,
,  ,
,
 ,
,  . (3,16)
. (3,16)
Непрерывный спектр.
Спектр положительных собственных значений непрерывен и простирается от нуля до бесконечности. Каждое из этих собственных значений вырождено с бесконечной кратностью; каждому значению  соответствует бесконечное множество состояний с
соответствует бесконечное множество состояний с  , пробегающими все целые значения от
, пробегающими все целые значения от  до
до  (и со всеми возможными, при данных
(и со всеми возможными, при данных  , значениями
, значениями  ).
).
|
|
Определяемое формулами (3,3) число  и переменная
и переменная  теперь чисто мнимы:
теперь чисто мнимы:
 ,
,  , (3,17)
, (3,17)
где  . Радиальные собственные функции непрерывного спектра имеют вид
. Радиальные собственные функции непрерывного спектра имеют вид
 (3,18)
(3,18)
где 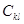 - нормировочный множитель. Они могут быть представлены в виде комплексного интеграла
- нормировочный множитель. Они могут быть представлены в виде комплексного интеграла
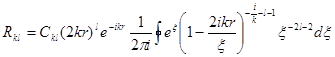 , (3,19)
, (3,19)
который берется по контуру (см. рис ниже).








Подстановкой  этот интеграл приводится к более симметричному виду
этот интеграл приводится к более симметричному виду
 (3,20)
(3,20)
(путь интегрирования обходит в положительном направлении точки  ). Из этого выражения непосредственно видно, что функции
). Из этого выражения непосредственно видно, что функции  вещественны.
вещественны.
Асимптотическое разложение вырожденной гипергеометрической функции позволяет непосредственно получить такое же разложение для волновой функции 

(3,21)
Если нормировать волновые функции «по шкале  », то нормировочный коэффициент
», то нормировочный коэффициент  равен
равен
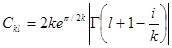 (3,22)
(3,22)
Действительно, асимптотическое выражение  при больших
при больших  (первый член разложения (3,21)) тогда имеет вид
(первый член разложения (3,21)) тогда имеет вид
 ,
,
(3,23)

в согласии с общим видом нормировочных волновых функций непрерывного спектра в центрально-симметричном поле. Выражение (3,23) отличается от общего вида наличием логарифмического члена в аргументе у синуса; поскольку, однако, 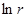 растет при увеличении
растет при увеличении  медленно по сравнению с самим
медленно по сравнению с самим  , то при вычислении нормировочного интеграла, расходящегося на бесконечности, наличие этого члена не существенно.
, то при вычислении нормировочного интеграла, расходящегося на бесконечности, наличие этого члена не существенно.
Модуль Г-функции, входящий в выражение (3,22) для нормировочного множителя, может быть выражен через элементарные функции. Воспользовавшись известными свойствами Г-функций
 ,
,  ,
,
имеем
 ,
,

и далее
 .
.
Таким образом,
 (3,24)
(3,24)
(при  произведение заменяется на 1).
произведение заменяется на 1).
Предельным переходом  можно получить радиальную функцию для особого случая равной нулю энергии. При
можно получить радиальную функцию для особого случая равной нулю энергии. При 


 ,
,
где  - функция Бесселя. Коэффициенты
- функция Бесселя. Коэффициенты  (3,24) при
(3,24) при  сводятся к
сводятся к

Отсюда находим
 (3,25)
(3,25)
Асимптотический вид этой функции при больших 
 (3,26)
(3,26)
Множитель 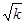 исчезает при переходе к нормировке «по шкале энергии», т.е. от функции
исчезает при переходе к нормировке «по шкале энергии», т.е. от функции  к функции
к функции  ; именно функция
; именно функция  остается конечной в пределе
остается конечной в пределе  .
.
В кулоновом поле отталкивания 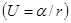 имеется только непрерывный спектр положительных собственных значений энергии. Уравнение Шредингера в этом поле может быть формально получено из уравнения для поля притяжения изменением знака у
имеется только непрерывный спектр положительных собственных значений энергии. Уравнение Шредингера в этом поле может быть формально получено из уравнения для поля притяжения изменением знака у  . Поэтому волновые функции стационарных состояний получаются непосредственно из (3,18) посредством этой же замены.
. Поэтому волновые функции стационарных состояний получаются непосредственно из (3,18) посредством этой же замены.
Нормировочный коэффициент снова определяется по асимптотическому выражению и в результате получается
 ,
,
 . (3,27)
. (3,27)
Асимптотическое выражение этой функции при больших  имеет вид
имеет вид
 ,
,
(3,28)
 .
.
Природа кулонова вырождения.
При классическом движении частицы в кулоновом поле имеет место специфический для этого поля закон сохранения; в случае поля притяжения
 (3,29)
(3,29)
В квантовой механике этой величине отвечает оператор
 (3,30)
(3,30)
коммутативный, как легко проверить, с гамильтонианом  .
.
Прямое вычисление приводит к следующим правилам коммутации для операторов  друг с другом и с оператором момента:
друг с другом и с оператором момента:
 ,
,  . (3,31)
. (3,31)
Некоммутативность операторов  друг с другом означает, что величины
друг с другом означает, что величины  не могут иметь в квантовой механике одновременно определенных значений. Каждый из этих операторов, скажем
не могут иметь в квантовой механике одновременно определенных значений. Каждый из этих операторов, скажем  , коммутативен с такой же компонентой момента
, коммутативен с такой же компонентой момента  , но некоммутативен с оператором квадрата
, но некоммутативен с оператором квадрата
момента  . Наличие новой сохраняющейся величины, не измеримой одновременно с другими сохраняющимися величинами,, приводит к дополнительному вырождению уровней, - это и есть специфическое для кулонова поля «случайное» вырождение дискретных уровней энергии.
. Наличие новой сохраняющейся величины, не измеримой одновременно с другими сохраняющимися величинами,, приводит к дополнительному вырождению уровней, - это и есть специфическое для кулонова поля «случайное» вырождение дискретных уровней энергии.
Происхождение этого вырождения можно сформулировать также и в терминах той повышенной симметрии (по сравнению с симметрией по отношению к пространственным вращениям), которой обладает кулонова задача в квантовой механике.
Для этого отмечаем, что для состояний дискретного спектра, с фиксированной отрицательной энергией, можно заменить  в правой стороне соотношения (3,31) на
в правой стороне соотношения (3,31) на  и ввести вместо
и ввести вместо  операторы
операторы  . Для них правила коммутации принимают вид
. Для них правила коммутации принимают вид
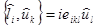 ,
,  (3,32)
(3,32)
Вместе с правилом  эти соотношения формально совпадают с правилами коммутации операторов бесконечно малых поворотов в четырехмерном евклидовом пространстве. Это и есть симметрия кулоновой задачи в квантовой механике.
эти соотношения формально совпадают с правилами коммутации операторов бесконечно малых поворотов в четырехмерном евклидовом пространстве. Это и есть симметрия кулоновой задачи в квантовой механике.
Из соотношений коммутации (3,32) можно снова получить выражение для уровней энергии в кулоновом поле. Перепишем их, введя вместо  и
и  операторы
операторы
 ,
,  . (3,33)
. (3,33)
Для них имеем
 ,
,  ,
,  (3,34)
(3,34)
Эти правила формально совпадают с правилами коммутации двух независимых векторов трехмерного импульса. Поэтому собственные значения каждого из квадратов  и
и 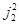 равны
равны  и
и 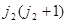 , где
, где  . С другой стороны, по определению операторов
. С другой стороны, по определению операторов  и
и  , находим, после простого вычисления:
, находим, после простого вычисления:
 ,
,

(при вычислении суммы  снова заменено
снова заменено  на
на  ). Отсюда
). Отсюда

(где  ) и затем
) и затем  .
.
Обозначив
 ,
,  , (3,35)
, (3,35)
приходим к требуемому результату  . Кратность вырождения уровней равна, как и следовало:
. Кратность вырождения уровней равна, как и следовало:  . Наконец, поскольку
. Наконец, поскольку  , то при заданном
, то при заданном  орбитальный момент пробегает значения от
орбитальный момент пробегает значения от  до
до  .
.
[1] Предполагается, что при малых  поле таково, что падения частицы не происходит.
поле таково, что падения частицы не происходит.