Построение решений обыкновенных дифференциальных уравнений
Решение дифференциального уравнения 1-го порядка
 ,
,  .
.
Простой метод Эйлера реализуется применением на каждом шаге вычислений следующих итерационных выражений:
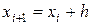 ,
,
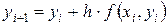 .
.
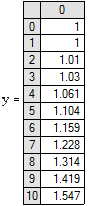
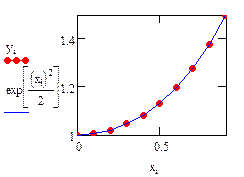
Рассмотрим реализацию метода в MathCADна примере уравнения:
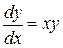 ,
, 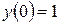 ,
, 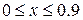 .
.
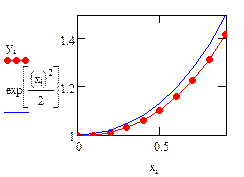
Аналитическое решение известно и имеет вид:
 .
.
Краткие сведения о составлении программ в MathCAD
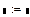 знак присваивает функции или переменной (они помещаются слева) выражение или число, которые помещаются справа. Набирается клавишей двоеточие «: » или из меню по цепочке View→ Toolbars→ Calculator.
знак присваивает функции или переменной (они помещаются слева) выражение или число, которые помещаются справа. Набирается клавишей двоеточие «: » или из меню по цепочке View→ Toolbars→ Calculator.
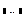 знак обозначает последовательное изменение переменной через единицу от значения слева до значения справа. Набирается клавишей точка с запятой «; ».
знак обозначает последовательное изменение переменной через единицу от значения слева до значения справа. Набирается клавишей точка с запятой «; ».
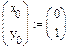 матрица вставляется командой меню Insert→ Matrix или клавишами Ctrl-M. Нижний индекс добавляется клавишей квадратная скобка «[ ».
матрица вставляется командой меню Insert→ Matrix или клавишами Ctrl-M. Нижний индекс добавляется клавишей квадратная скобка «[ ».
График вставляется командой Insert→ Graph→ X-YPlot или клавишей «@ ».
Для удобства в работе рекомендуется отключить автоматическое вычисление, убрав галочку с опции меню Tools→ Calculate→ AutomaticCalculation. Тогда расчет не будет выполняться в ходе набора программы, а запуститься только после нажатия кнопки Calculate, расположенной на панели инструментов (в виде значка  ).
).
Ниже приведена расчетная программа. Повторите её. Получите графики с тем же форматом линий. Формат линий графика можно изменить, открыв с помощью ПК мыши контекстное меню и выбрав Format… → Traces.
Программа для простого метода Эйлера
| Функция, определяющая производную
|
| Задание начальных условий
|
Следующая программа реализует модифицированный метод Эйлера. Отличие от простого метода заключается в итерационных уравнениях.
Программа для модифицированного метода Эйлера
| Функция, определяющая производную
|
| Задание начальных условий
|
Метод Рунге-Кутта 4-го порядка используется в тех случаях, когда необходима высокая точность расчетов, недостигаемая методами Эйлера.
Программа для метода Рунге-Кутта
| Функция, определяющая производную
|
| Задание коэффициентов k1, k2, k3, k4 как функций пользователя:
|
| Задание начальных условий
|
Решение дифференциальных уравнений 2-го порядка методом Рунге-Кутта.
Подход к реализации метода основан на использовании дополнительной функции  . Это позволяет перейти к системе уравнений, содержащих только первые производные. Итак, пусть требуется найти решение задачи:
. Это позволяет перейти к системе уравнений, содержащих только первые производные. Итак, пусть требуется найти решение задачи:
 ,
,  ,
, 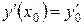 .
.
Преобразуем задачу к системе из двух уравнений:
 ,
,  ,
,
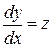 ,
,  .
.
Тогда получим следующее обобщение итерационной схемы:
 .
.  ,
,
где
 ,
, 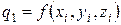 ,
,
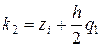 ,
,  ,
,
 ,
,  ,
,
 ,
, 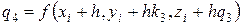 .
.
Отметим, что значения на каждом следующем шаге рассчитываются по значениям, полученным на предыдущем. Кроме того, использованы прежние правила «взвешивания» коэффициентов при усреднении.
Пример математической модели с дифференциальным уравнением 2-го порядка
Рассмотрим уравнение колебательного процесса при наличии внешнего периодического воздействия:
 ,
,
где t – время, и искомой является зависимость  ;
;
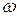 – круговая частота собственных колебаний;
– круговая частота собственных колебаний;
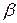 – круговая частота внешнего воздействия с амплитудой «a ».
– круговая частота внешнего воздействия с амплитудой «a ».
Если 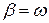 , то общее решение уравнения имеет вид (проверьте подстановкой):
, то общее решение уравнения имеет вид (проверьте подстановкой):
 ,
,
где A и 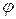 – произвольные постоянные. Частное решение выбирается заданием значений этих постоянных. Второе слагаемое решения показывает, что с течением времени амплитуда колебаний неограниченно возрастает. Это явление называется резонансом.
– произвольные постоянные. Частное решение выбирается заданием значений этих постоянных. Второе слагаемое решения показывает, что с течением времени амплитуда колебаний неограниченно возрастает. Это явление называется резонансом.
Когда  , общее решение имеет вид:
, общее решение имеет вид:
 .
.
В этом случае колебательный процесс слагается из собственных колебаний с частотой 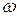 и вынужденных с частотой
и вынужденных с частотой 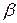 .
.
Моделирование резонансных колебаний
Методом Рунге-Кутта найдем решение задачи:
 ,
, 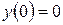 ,
,  ,
,  .
.
Согласно изложенной выше теории, аналитическое решение уравнения имеет вид:
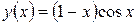 .
.
Ниже приведен алгоритм расчета и его реализация в MathCAD.
Программа расчета резонансных колебаний методом Рунге-Кутта
| Функция в системе уравнений dy/dx = z и dz/dx = f(x,y,z)
|
| Задание коэффициентов как функций пользователя:
|
| Задание начальных условий
|
Задание для самостоятельного выполнения
Найти решение уравнения вынужденных колебаний:
 ,
, 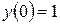 ,
, 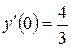 ,
, 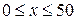 .
.
Решение представить в виде графика. Для сравнения привести и график точного решения (также как это было сделано для резонансных колебаний).
 ,
,  .
.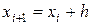 ,
,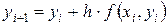 .
.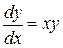 ,
, 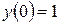 ,
, 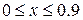 .
. .
.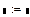 знак присваивает функции или переменной (они помещаются слева) выражение или число, которые помещаются справа. Набирается клавишей двоеточие «: » или из меню по цепочке View→ Toolbars→ Calculator.
знак присваивает функции или переменной (они помещаются слева) выражение или число, которые помещаются справа. Набирается клавишей двоеточие «: » или из меню по цепочке View→ Toolbars→ Calculator.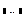 знак обозначает последовательное изменение переменной через единицу от значения слева до значения справа. Набирается клавишей точка с запятой «; ».
знак обозначает последовательное изменение переменной через единицу от значения слева до значения справа. Набирается клавишей точка с запятой «; ».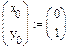 матрица вставляется командой меню Insert→ Matrix или клавишами Ctrl-M. Нижний индекс добавляется клавишей квадратная скобка «[ ».
матрица вставляется командой меню Insert→ Matrix или клавишами Ctrl-M. Нижний индекс добавляется клавишей квадратная скобка «[ ». ).
).





















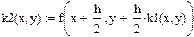

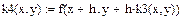







 . Это позволяет перейти к системе уравнений, содержащих только первые производные. Итак, пусть требуется найти решение задачи:
. Это позволяет перейти к системе уравнений, содержащих только первые производные. Итак, пусть требуется найти решение задачи: ,
,  ,
, 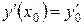 .
. ,
,  ,
,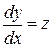 ,
,  .
. .
.  ,
, ,
, 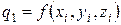 ,
,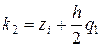 ,
,  ,
, ,
,  ,
, ,
, 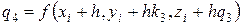 .
. ,
, ;
;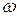 – круговая частота собственных колебаний;
– круговая частота собственных колебаний;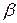 – круговая частота внешнего воздействия с амплитудой «a ».
– круговая частота внешнего воздействия с амплитудой «a ».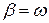 , то общее решение уравнения имеет вид (проверьте подстановкой):
, то общее решение уравнения имеет вид (проверьте подстановкой): ,
,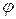 – произвольные постоянные. Частное решение выбирается заданием значений этих постоянных. Второе слагаемое решения показывает, что с течением времени амплитуда колебаний неограниченно возрастает. Это явление называется резонансом.
– произвольные постоянные. Частное решение выбирается заданием значений этих постоянных. Второе слагаемое решения показывает, что с течением времени амплитуда колебаний неограниченно возрастает. Это явление называется резонансом. , общее решение имеет вид:
, общее решение имеет вид: .
.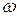 и вынужденных с частотой
и вынужденных с частотой 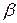 .
. ,
, 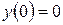 ,
,  ,
,  .
.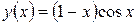 .
.

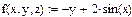
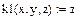








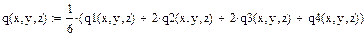


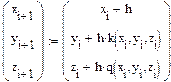

 ,
, 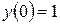 ,
, 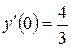 ,
, 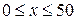 .
.