Решение уравнения Блазиуса для сжимаемого газа
Покровский А.Н. (МАТИ-РГТУ имени К.Э.Циолковского)
Настоящая работа выполнена с использованием идей Х.А.Рахматулина, учеником которого автор является. В известных работах, посвященных рассматриваемой задаче, представлено аналитическое решение уравнений пограничного слоя при линейной зависимости вязкости газа от температуры [1], а также уравнений, полученных с использованием асимптотических разложений [2] и численным методом [3]. Рассмотрим способ представления решений уравнений различных краевых задач с учётом степенной зависимости вязкости от температуры, а также проанализируем свойства полученных численным методом решений.
В случае исследования высокоскоростного газового потока при низкой температуре стенки, т.е. когда нельзя пренебречь изменением величины rm в поперечном направлении пограничного слоя (m ~ hn), система уравнений, описывающая течение в пограничном слое на поверхности плоской пластины, принимает вид [1, 4]:
(1)
(2)
с граничными условиями
f = d1, f¢ = l, g = gw при h = 0 (3)
f¢ ® 1, g ® 1 при h ® ¥,
где f – безразмерная функция тока,
h - координата подобия,
g – относительная полная энтальпия газа,
h - энтальпия газа,
ad - число Крокко,
n – показатель степени в зависимости вязкости от энтальпии.
Общее решение системы (1, 2) с граничными условиями (3) при d1 = l = 0 (неподвижная стенка без вдува) будет таким:
, (4)
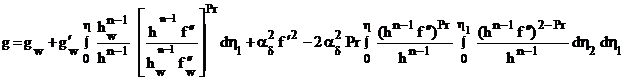Систему (1, 2) можно также решить итерационным методом, задав приближенное значение функции h и определив функцию f (4), а затем g. После этого находится новое значение h и, соответственно, f и g. Однако этот процесс является весьма трудоемким, поэтому можно поступить другим способом. Поскольку h1-n - слабо меняющаяся функция, удобнее ввести некоторое среднее её значение, отвечающее поперечному сечению пограничного слоя, т.е.
.
Это значительно облегчает отыскание коэффициентов трения Cf и теплообмена St. Действительно, рассмотрев первое приближение решения поставленной задачи, найдем
Исходя из внешнего граничного условия, получим
. (5)
Выведем далее уравнение для определения функции g в системе (1), (2). Использование предположения о постоянстве hcр позволяет представлять g при числах Рr, не сильно отличающихся от 1, в виде:
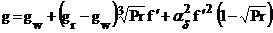, где gr - отношение полной энтальпии теплоизолированной стенки к полной энтальпии потока.
Выражение hср может быть представлено в виде
.
Проинтегрировав его, получим
.
В данной формуле неизвестны f(h k), h k и a. Они должны быть найдены в ходе решения задачи. Если Рr = 1, то последнее выражение переходит в соответствующую формулу для расчета hср, предложенную Янгом ([4], с. 342), при этом f(h k)/ h k = 0,45 и a/hk = 0,18. Подставив упомянутые значения в приведенную формулу, получим следующее выражение hср.
. (6)
Таким образом, уравнения (5) и (6) позволяют определять коэффициент трения Сf при произвольных числах М¥, gr, gw, Рr. Коэффициент теплообмена St находится исходя из соотношения 
.
Рассмотрим анализируемую задачу при наличии вдува или отсоса газа с поверхности пластины. Общее решение имеет вид
.
Ограничившись первым приближением решения данной задачи, найдем соотношение, определяющее параметр a1
которое можно представить следующим образом:
(7)
Процедура нахождения hср такая же, как было описано выше, поэтому окончательное его выражение будет таким:
. (8)
Таким образом, уравнения (7, 8) позволяют определять коэффициент трения Сf на пластине при наличии вдува или отсоса газа.
Перейдем к рассмотрению последней задачи, связанной с решением уравнений (1, 2) применительно к движущейся поверхности пластины. Одно из граничных условий при этом изменится на f¢ = l при h = 0, остальные останутся без изменения. Общее решение уравнения (1), (2) имеет вид:
Заменив функцию h на некоторое среднее её значение hср в первом приближении найдём
Это уравнение можно представить так:
,
где hср определяется так же, как и в основном варианте, формулой (8), а 
.
Таким образом, представлены необходимые формулы для расчета коэффициентов трения и теплообмена на поверхности плоской пластины при наличии вдува (отсоса) газа, а также на движущейся её поверхности с учётом зависимости m ~ hn. Предложенные формулы позволяют определять Сf и St при самых разнообразных граничных условиях.
Рассмотрим численное исследование краевой задачи (1)–(3). Воспользовавшись параметрическим методом пристрелки [5], исследуем влияние относительной скорости движения пластины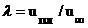 
при различных законах изменения вязкости в зависимости от энтальпии газа (m ~ hn). На рис. 1 продемонстрирована зависимость величины 
от показателя n при изменении величины h поперек пограничного слоя. Начальные параметры: М¥ = 10; Pr = 1; gw = 1. Видно, что с уменьшением n значения увеличиваются, а кривые = (l) имеют качественно такой же характер, как и при n = 1. Относительная скорость l движения пластины навстречу набегающему потоку, при которой получено автомодельное решение, незначительно снижается.
 |
Рис. 1 Влияние относительной скорости движения пластины l на
величину 
, пропорциональную коэффициенту трения сf
при различных законах изменения вязкости от температуры (n)
Влияние относительного вдува газа d на величину отражено на рис. 2 при тех же начальных параметрах. Видно, что с уменьшением n величина увеличивается при d > -0,28 и уменьшается при d < -0,28, асимптотически приближаясь к нулю. Фрагмент зависимости (l) при d < -0,1 показан на рис. 3.
Рис. 2 Влияние относительного вдува газа d на величину ,
пропорциональную коэффициенту трения сf при
различных законах изменения вязкости от температуры (n)
 |
Рис. 3 Зависимости fwn (d) при отрицательных значениях параметра вдува d
Влияние отрицательного параметра l на величину при других значениях исходных параметров d = -0,1; n = 0,7; gw = 0,8; Pr = 0,7; M¥=10 иллюстрирует рис. 4 (кривая 1). Заметим, что при l < -0,28 автомодельного решения не существует. Такой же характер имеет кривая = (d) (кривая 2, l = -0,1). Остальные параметры имели те же значения, что и при построении кривой 1. Видно, что в этом случае автомодельного решения не существует при d < -0,355.
Рис. 4 Влияние относительной скорости движения пластины l (1)
на параметр f"w при d = -0,1.
Влияние относительного вдува газа d (2) на параметр f"w
при l = -0,1; n = 0,7; qw = 0,8; Pr = 0,7; M¥ = 10
Таким образом, в данной работе представлено аналитическое решение уравнений, описывающей пограничный слой на движущейся стенке, при наличии вдува или отсоса газа. На основании численного решения найдены границы области существования автомодельного решения.
Работа выполнена при финансовой поддержке гранта Российского фонда фундаментальных исследований (проект № 07-01-00312).
ЛИТЕРАТУРА
1. Покровский А.Н. Об одном представлении решения уравнения Блазиуса и его приложениях. - Изв. АН СССР. МЖГ, 1975, № 3, с. 143-146.
2. Черный Г.Г. Пограничный слой на движущейся поверхности. Механика жидкости и газа, Избранное, К 80-летию академика РАН Г.Г.Черного, Части I и II, М., Физматлит, 2003, 752 с.
3. Casal. P. Sur l'ensemble des solutions de l'equation de la couche limite. - J. Mecanique, 1972, v. 11, № 3, с. 459-469.
4. Лойцянский Л.Г. Ламинарный пограничный слой. М. Физматлит, 1962, 480 с.
5. Ц. На Вычислительные методы решения прикладных граничных задач. М.: Мир, 1982, 296 с. ∞∞
Темы по дисциплине «Теория пограничного слоя »
Для расчетно-графических работ гр. Т30- 101М-16
1. Анализ влияния чисел Маха М; M¥ =2(d2)10 и угла полураствора
Конуса TETA= 5(d5)20 на коэффициенты трения Cf и теплообмена
St. L=20r0 , где r0 - радиус притупления носка тела (r0 =0.03м.)
Числа Рейнольдса ReL∞:104 < ReL∞ < 107. В средней точке x=10rO
построить профили скорости и температуры в пограничном слое.
2. Определение коэффициентов трения и теплообмена на крылатых
летательных аппаратах (ЛА) с учетом переходного слоя. Стреловид-
ность 700, числа Маха M¥ =2(d2)6; gw =0.8, где r0 - радиус
притупления носка тела (r0 =0.03м.) Числа Рейнольдса RеL∞
104 < ReL∞ < 107 . Углы полураствора конуса TETA= 5(d5)20.
3. Исследование влияния шероховатости поверхности на параметры
пограничного слоя. Числа Маха М; M¥ =2(d2)10 и углы полураствора
конуса TETA= 5(d5)20 на коэффициенты трения Cf и теплообмена
St. L=20r0 , где r0 - радиус притупления носка тела (r0 =0.03м.)
. Числа Рейнольдса ReL∞:104 < ReL∞ < 107. В средней точке x=10rO
построить профили скорости и температуры в пограничном слое.
4. Моделирование ближнего и дальнего следа за осесимметричными
Телами и расчет донного сопротивления при сверхзвуковых
скоростях обтекания. Числа Маха М; M¥ =2(d2)10 и углы полу-
раствора конуса TETA= 5(d5)20 на коэффициенты ламинарного и
турбулентного донного давления Cxd . L=20r0 , где r0 - радиус
притупления носка тела (r0 =0.03м.) Числа Рейнольдса ReL∞:
104 < ReL∞ < 107.
5. Исследование влияния пульсаций набегающего потока на параметры
пограничного слоя. Числа Маха М; M¥ =2(d2)10 и углы полураствора
конуса TETA= 5(d5)20 на коэффициенты трения Cf и теплообмена
St. L=20r0 , где r0 - радиус притупления носка тела (r0 =0.03м.)
. Числа Рейнольдса ReL∞:104 < ReL∞ < 107. В средней точке x=10rO
построить профили скорости и температуры в пограничном слое.
6. Определение нестационарных параметров невязкого течения в
ударном слое, нестационарных аэродинамических характеристик и
параметров нестационарного пограничного слоя на тонких
затупленных конусах, совершающих малые колебания около нулевого
угла атаки в сверхзвуковом потоке газа.. Числа Маха М; M¥ =2(d2)10
и углы полураствора конуса TETA= 5(d5)20 на коэффициенты
трения Cf и теплообме St. L=20r0 , где r0 - радиус притупления
носка тела (r0 =0.03м.). Числа Рейнольдса ReL∞:104 < ReL∞ < 107.