Краткое описание и цели
Цель: составлять и решать линейные уравнения при решении задач.
Задачи:
· составлять математические модели (уравнения)по условиям текстовых задач;
· интерпретировать результат;
· составлять выражения по условиям задач с буквенными данными;
· комментировать ход преобразований.
Образовательные стандарты
1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.
Теоретический материал для самостоятельного изучения.
Мы уже рассматривали примеры функциональных зависимостей между величинами как математические модели реальных процессов. Теперь рассмотрим текстовые задачи, математическими моделями которых являются линейные уравнения и уравнения, сводящиеся к линейным.
Решить задачу можно с помощью системы уравнений, а можно с помощью одного уравнения. Рассмотрим на примере задачи.
Задача 1.
Из города А в город В одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 15 км/ч, а вторую половину пути – со скоростью 90 км/ч, в результате чего прибыл в В одновременно с первым автомобилем. Найдите скорость первого автомобиля, если известно, что она больше 54 км/ч. Ответ дайте в км/ч.
При решения текстовых задач эффективно построение схем и составление таблиц.
Используя сравнение скоростей, указанное в задаче, и обозначая скорость первого автомобиля икс, запишем скорость второго автомобиля на протяжении всего пути:
Скорость первого автомобиля: x, скорость второго автомобиля: x – 15x – 15/
Теперь заполним вспомогательную таблицу.

Условие, что автомобили прибыли в пункт назначения одновременно, используем для составления уравнения. Выражаем время первого автомобиля, которое он затратил на весь путь, через x.
Время первого автомобиля:
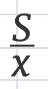
Время второго автомобиля:
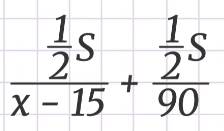
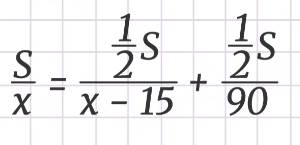
Сократим на S ≠ 0 и умножим на 2.
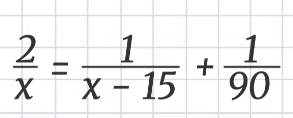
Умножим обе части на 90x(x – 15), получим:
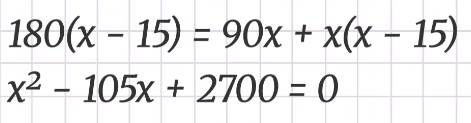
Решением уравнения будут корни:
x1 = 60, x2 = 45.
Условию уравнения удовлетворяет только x = 60
Ответ: 60 км/ч – скорость первого автомобиля.
Составим алгоритм решения текстовых задач при помощи уравнений.
Решать задачу с помощью уравнения следует в такой последовательности:
1) обозначить переменной одну из неизвестных величин;
2) другие неизвестные величины (если они есть) выразить через введенную переменную;
3) по условию задачи установить соотношение между неизвестными и известными значениями величин и составить уравнение;
4) решить полученное уравнение;
5) проанализировать решение уравнения и найти неизвестную величину, а при необходимости и значения остальных неизвестных величин;
6) записать ответ к задаче.
Дополнительный материал.
Решите задачу двумя способами.
В первый день со склада было отпущено 20% имевшихся груш. Во второй день 180% от того количества груш, которое было отпущено в первый день. В третий день ‑ оставшиеся 88 кг. Сколько кг груш было на складе первоначально?
Разберем 2 способа решения этой задачи.
Для первого способа составим вспомогательную таблицу:
Значит, первоначально было 200 кг груш.
2 способ.
Составим вспомогательную аблицу:


Ответ: 200 кг груш.
Практика
Выполнить задачи №148, № 154
