У нас имеется исходный набор простейших (базисных)вычислимых функций. Мы будем пополнять этот наборвычислимых функций. Для этого рассмотрим способыпостроения из уже имеющихся вычислимых функций новых вычислимых функций. Оператор суперпозиции S. Рассмотрим действие,которое назовем оператором суперпозиции (регулярной суперпозиции). С помощью этого действия из некоторых функций h, g1, g2,..., gm создается новая функция f. Пусть m, n – натуральные числа. Определим новую функцию f(x1,x2,...,xn) по правилу: f(x1,x2,...,xn)=h(g1(x1,x2,...,xn),g2(x1,x2,...,xn),...,gm(x1,x2,...,xn)).
Функция f является частичной функцией от n переменных. Ее значение f(x1,x2,...,xn) определено тогда и только тогда, когда определены все выражения в правой части из последнего равенства. Если функции h, g1,
g2,..., gmвычислимы, то и функция f вычислима. Алгоритм ее вычисление
описывается правой частью равенства. В случае существования значения функции f, мы за конечное число шагов получим число f(x1,x2,...,xn) действиями, соответствующими интуитивному представлению об алгоритме.
57) Определение примитивно-рекурсивной функции. Функция f называется примитивно рекурсивной, если она может быть получена из простейших функций следования, нулевой функции и функции проектирования с помощью конечного числа применений операторов суперпозиции и примитивной рекурсии. Тоже самое можно выразить в виде трех правил. 1) Простейшие функцииs(x)=x+1, on(x1,x2,...,xn)=0, In
m (x1,x2,...,xn)=xm примитивно рекурсивны. 2) Если функция f получена из примитивно рекурсивных функций с помощью оператора суперпозиции или с помощью оператора примитивной рекурсии, то функция f примитивно рекурсивна. 3) То, что функция f примитивно рекурсивна, устанавливается несколькими применениями правил 1) и 2). Всякой примитивной рекурсивной функции можно приписать n -наименьший номер шага, на котором она может быть получена. Следовательно, можно проводить доказательство различных утверждений для примитивно рекурсивных функций индукцией по шагу, на котором они получены.
58) Примеры примитивно-рекурсивных функций. Теорема 1. Следующие функции являются примитивно рекурсивными:
1. f(x)=x;
2. g(x)=x+2;
3. Постоянная унарная функция f(x)=a;
4. Нульарная функция.
Операция введения фиктивныхпеременных Пусть функция f(x1,x2,...,xn) примитивно рекурсивна. Добавим в строке
переменныхf(x1,x2,...,xn) еще одну переменную xn+1. Получим строку x =(x1,x2,...,xn,xn+1) из n+1 переменной. Для функций проектирования очевидны n равенств In+1 (x)=x1,..., In+1n (x)=xn. Введем функцию f’(x) от n+1 переменной правилом f’ (x1,x2,...,xn,xn+1)=f(In+1 (x)=x1,..., In+1n (x))= f(x1,x2,...,xn). Так как функция f примитивно рекурсивна, то и новая функция f’ примитивно рекурсивна. В дальнейшем мы будем вводить фиктивную переменную, и из примитивно рекурсивной функции от n переменных получать примитивно рекурсивную функцию от n+1 переменной. При такой операции введения фиктивного переменной вместо обозначения f’ для новой функции будем сохранять обозначение f исходной функции.Еще две примитивно рекурсивные функции Теорема 2. Функция сложения f(x,y)=x+y и функция умножения f(x,y)=xy примитивно рекурсивны.
59) Частично-рекурсивные функции. Тезис Черча. Пусть дана вычислимая функция g(x1,x2,...,xn,y) от n+1 переменной, где n0. Нам нужно найти наименьшее число y с условием g(x1,x2,...,xn,y)=0. Введем следующее ограничение. Процедура нахождения числа y должна быть алгоритмом. Поэтому должен быть представлен точный список действий для неинтеллектуального исполнителя (машины) по нахождению y,например, последовательная проверка одного за другим следующих равенств
g(x1,x2,...,xn,0)=0,
g(x1,x2,...,xn,1)=0,
.............................
g(x1,x2,...,xn,y)=0.
Что при этом произойдет? Возможно, вообще нет числа y с условием g(x1,x2,...,xn,y)=0. Тогда не произойдет остановки машины с выдачей y. Однако отсутствие y возможно по другой причине. Предположим, например, что g(x1,x2,...,xn,5)=0,, а значение g(x1,x2,...,xn,2) не определено. Пытаясь вычислить g(x1,x2,...,xn,2) машина будет работать бесконечно и никогда не перейдет к вычислению g(x1,x2,...,xn,3). Поэтому число y=5 не будет обнаружено.
60)Оператор минимизации. Определение.Пусть g - функция от n+1 переменной. Будемговорить, что функция f от n переменных получена из функции g с помощью оператора минимизации,если равенство f(x1,x2,...,xn)=y верно тогда и только тогда, когда g(x1,x2,...,xn, y) =0, а значения g(x1,x2,...,xn,0),..., g(x1,x2,...,xn,y-1)определены и не равны нулю. Если функция f получается из функции g с помощью оператора минимизации, то записываем f=M(g). Ясно, что инструкции для вычисления функции g и проверки выполнения процедуры минимизации образуют алгоритм для вычисления значений функции f. Поэтому функция f вычислима.
61) Пример применения оператора минимизации. Пример. Найти функцию f, полученную из функции o(x) применением оператора минимизации. Решение. Если функция f получена из функции g с помощью оператора минимизации, то число ее переменных меньше числа переменных функции g на единицу. В данном случае g – это функция o(x) от одной переменной. Поэтому функция f имеет 0 переменных. Для нахождения значения функции f нужно проверить условия o(0)=0, o(1)=0,..., o(y)=0 и выбрать в этих равенствах наименьшее y. Поскольку o(x)=0 для всех x, то наименьшее число y - это y=0. По определению оператора минимизации полученное y=0 и есть значение функции f. Поэтому функция f - это нульарная функция o0 со значением 0, т.е. помеченный элемент 0.
62) Машины Тьюринга Другой способ для обоснования понятия алгоритма предложили независимо друг от друга и почти одновременно с Черчем и Клини английский математик А. Тьюринг и американский математик Э. Пост. Основная идея Поста и Тьюринга заключалась в том, что алгоритмические процессы – это процессы, которые может совершать некоторая «машина». Машины, введенные Постом и Тьюрингом, имеют не очень существенное различие и обычно называются машинами Тьюринга.
63) Описание машины Тьюринга. Машина Тьюринга - это воображаемое вычислительное устройство, имеющее следующие составные части. Оно имеет ленту, разбитую на ячейки, и каретку, расположенную в каждый конкретный момент работы машины над некоторой ячейкой ленты.
Каждая ячейка содержит ровно один из символов 0 или 1. Лента представляется конечной, но дополняемой в любой момент ячейками слева и справа для записи новых символов 0 или 1. Эта ситуация может возникнуть при сдвиге каретки влево или вправо за край ленты. Тогда наращивается новая клетка с содержимым 0. Это соглашение отражает идею о сколь угодно большой, но конечной памяти. Если каретка, расположена над некоторой ячейкой с символом 0 (с символом 1), то говорим, что каретка обозревает символ 0 (обозревает символ 1).
64) Программы машины Тьюринга. Машина Тьюринга имеет программу. Это конечная последовательность инструкций q1, q2,...,qn, каждая из которых является строкой из компонент: (i, a, x, y, z), где i – номер инструкции;
a =0, или a=1;
x=0, или x=1;
у= L или y=R;
z – номер инструкции.
65) Вычисление значений функций. Рассмотрим алгоритм вычисления значений функций на машине Тьюринга. Сначала договоримся о представлении натуральных чисел на ленте: 1) натуральное число 0 будем изображать одной единицей, число 1 – двумя единицами, и т. д., натуральное число x – (x+1) - ой единицей:
2) Для изображения упорядоченной последовательности (x1, x2,..., xn) будем каждую группу единиц отделять друг от друга нулем. Пример. Так выглядит на ленте тройка чисел (3, 1, 10):
1 1 1 1 0 1 1 0 1 1 1 1 1 1 1 1 1 1 1
Пусть дана n-арная функция f(x1,x2,..., xn). Будем говорить, что машина Тьюринга M вычисляет функцию f, если выполняются следующие условия.
1. Пусть строка (x1,x2,..., xn) содержится в области определения функции f. Тогда машина M, начиная работать и обозревая левую единицу строки (x1,x2,...,xn) (остальная часть ленты пуста), на некотором шаге останавливается, обозревая левую единицу строки f(x1,x2,..., xn) (часть ленты справа от строки пуста). 2. Пусть строка (x1,x2,..., xn) не содержится в области
определения функции f. Тогда машина M работает
бесконечно.
65) Пример вычисление функции на машине Тьюринга. Построим машину Тьюринга, вычисляющую значения функции f(x,y)=x+y. Пусть на ленте находятся два числа x и y. Очевидно, что складывая эти числа мы должны устранить между ними 0 и уменьшить число единиц на два. В результате на ленте должно остаться (x+y+1) единиц, идущих последовательно друг за другом. Сначала проходим через x:(0, 1, 1, R,0). Эта инструкция повторится ровно x раз. Затем каретка окажется над нулем,разделяющим числа x и y. Этот ноль заменяем единицей с помощью инструкции: (0, 0, 1, R, 1). Теперь проходим через число y:(1, 1, 1, R, 1). Доходим до конца числа y. Каретка снова оказалась над нулем. Возвращаемся на одну ячейку назад и стираем одну, а затем еще одну единицу: (1, 0, 0, L,2), (2, 1, 0, L,3),(3, 1, 0, L,4). После стирания двух единиц можно вернуться назад и остановиться: (4, 1, 1, L, 4), (4, 0, 0, R,5).
67) Тезис Тьюринга. Теперь мы располагаем всеми необходимыми определениями для точной формулировки понятия алгоритма. Из определения машины Тьюринга легкоубедиться, что ее работа удовлетворяет всем требованиям, предъявляемым кпонятию алгоритма. Поэтому произвольная функция, вычислимая на машинеТьюринга, является вычислимой функцией. Рассмотрим обращение этогоутверждения. Тезис Тьюринга. Если функция f является вычислимой, то существует машина Тьюринга вычисляющая функцию f. Сможем ли мы доказать тезис Тьюринга? Нет, т.к. у нас нет точного определения понятия вычислимой функции. Тезис Тьюринга является результатом, возникшимиз опыта. Тезис Тьюринга - еще один вариант определения алгоритма, поскольку отождествляет интуитивное понятие вычислимой функции со строгим понятием функции, вычислимой на машине Тьюринга. Доказана равносильность тезиса Тьюринга и тезиса Черча. Это подкрепляет уверенность в том, что оба тезиса адекватно отражают понятие алгоритма. Тезисы Тьюринга и Черча можно рассматривать как теоретические границы возможностей реальных вычислительных машин.
68) Конфигурация машины Машинным словом, или конфигурацией машины M, называется слово вида AqkalB, где A и B - слова в алфавите A. Так изображается содержимое ленты и обозреваемая ячейка. При этом считаем, что машина находится в состоянии qk, а каретка обозревает на ленте символ al. Слова A и B отражают содержимое ленты до и после символа al. Группу из x символов a на ленте будем обозначать через ax.
69) Применение машины Тьюринга к словам Задача 1. Имеется машинаТьюринга с внешнималфавитом A={a0, 1} с алфавитом внутренних состояний Q={q0, q1} ипрограммой, представленной в таблице. Определить в какие словаперерабатывает программа каждое из следующихслов:
1) 1 a0 11 a0 a0 11 (4 ячейка) 2) 1 a0 111 a0 a0 11 (2 ячейка) 3) 1 a0 a0 111 (3 ячейка)
70) Машины с неограниченными регистрами. Машина с неограниченными регистрами (МНР) – это абстрактная машина, более
сходная с реальным компьютером по сравнению с машиной Тьюринга. Она имеет следующие составные части. 1) Регистры R1, R2,..., в которых содержатся соответственно натуральные числа r1, r2,.... Число регистров бесконечно, но только конечное множество регистров R1, R2,... Rk содержит числа, отличные от нуля. Все остальные регистры заполнены нулями.
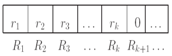Программа машины – это конечная последовательность I1, I2,..., Is. Из следующих четырех типов команд:
Z(n), S(n), T(m, n), J(m, n, q), где m, n, q \{1,2,... }. Эти команды выполняют следующие действия. Команда обнуленияZ(n) делает содержимое регистра Rn равным нулю. Команда прибавления единицы S(n) к содержимому регистра Rn прибавляет число1. Команда переадресацииT(m, n) заменяет содержимое регистра Rn на содержимое регистра Rm. Команда условного перехода J(m, n, q) сравнивает содержимое регистров Rm и Rn. При rm = rn в качестве следующей команды выполняется команда с номером q, в противном случае выполняется следующая по порядку команда программы.
Команды обнуления, прибавления единицы и переадресации называются
арифметическими командами.