Лекция 9
Индуктивность коаксиального кабеля.
По внутренней жиле коаксиального кабеля радиуса R 1 (рис. 9–3) протекает ток в одном направлении, а по наружной оболочке толщиной (R 3 – R 2)такой же ток в обратном направлении.
В каждой области элементарный магнитный поток может быть определен из соотношения:
d Ф = B·dS = m0· H·l·dr.
Запишем выражение для напряженности магнитного поля и найдем потокосцепление для каждой области внутри кабеля.
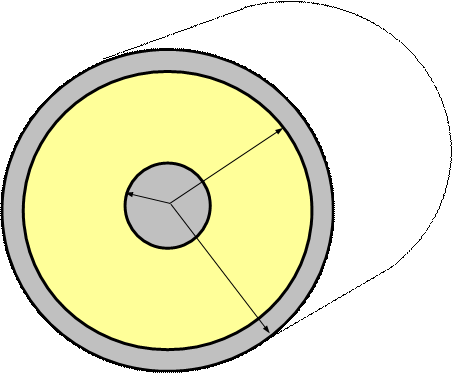
R 2
R 1
l
R 3
Рисунок 9–3
Первая область – внутри прямого проводника с током (0 £ r £ R1).
В этой области напряженность магнитного поля возрастает по линейному закону при удалении от оси кабеля:
; 
; 
; 
.
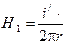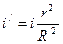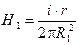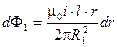Элементарный магнитный поток в первой области проходит внутри проводника, магнитная проницаемость которого обычно равна m0, и сцепляется лишь с частью всего тока внутренней жилы, определяемой отношением площади, охваченной линиями индукции соответствующего радиуса к площади сечения всей внутренней жилы. Поэтому потокосцепление внутренней жилы можем записать в виде:
.
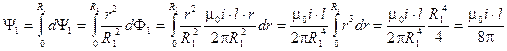Последнее соотношение определяет внутреннее потокосцепление провода кругового сечения с постоянным током, равномерно распределенным по его сечению.
Вторая область - в слое изоляции кабеля (R1 £ r £ R2)
В этой области напряженность магнитного поля убывает при удалении от оси кабеля, а элементарный магнитный поток равен элементарному потокосцеплению, так как сцепляется со всем током, проходящим по жиле кабеля, и является внешним по отношению к проводнику с током:
; 
; 
; 
.
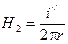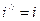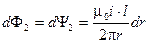Внешнее потокосцепление коаксиального кабеля, определяемое магнитным потоком в рассматриваемой области равно:
|
|
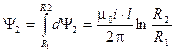
Третья область – внутри проводника (оболочки) с обратным током (R2 £ r £ R3)
В этой области напряженность магнитного поля зависит от обратного тока:
; 
; 
; 
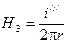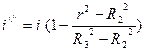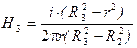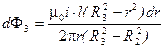
Элементарный магнитный поток сцепляется с прямым током (+ i) и с частью обратного тока (– i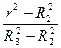 
), поэтому можем записать:
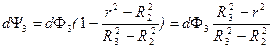
В результате интегрирования получим потокосцепление в третьей области:
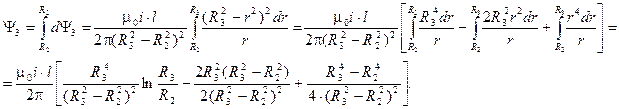
Упрощая, запишем окончательно: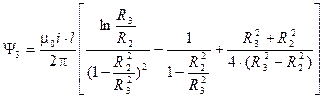 
.
Индуктивность коаксиального кабеля получим, разделив сумму всех составляющих потокосцепления на величину тока в кабеле:
.
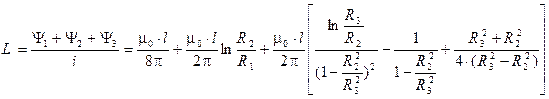Первое слагаемое в полученной сумме называется внутренней индуктивностью прямолинейного провода кругового сечения:
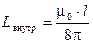
Следует подчеркнуть, что внутренняя индуктивность круглого прямолинейного провода не зависит от его радиуса, а определяется лишь длиной и магнитной проницаемостью материала проводника
Индуктивности тонких проводников с токами
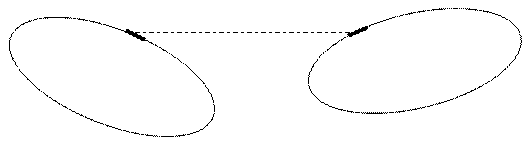
Определение взаимной индуктивности между тонкими контурами. Контур считается тонким, если поперечные размеры проводника намного меньше его длины. Рассмотрим два тонких контура (рис.9–4) и определим магнитный поток и потокосцепление второго контура от тока, протекающего в первом контуре, записав предварительно выражение для векторного магнитного потенциала, создаваемого этим током:
r
dl 1 dl 2
l 1 l 2
Рисунок 9–4
; 
.
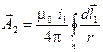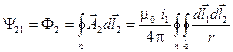Величина взаимной индуктивности между тонкими контурами определяется следующим соотношением:
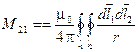
Определение индуктивности тонкого контура. В рассматриваемом случае формулу, полученную для взаимной индуктивности тонких контуров, нельзя непосредственно применить для определения собственной индуктивности, как мы это делали ранее, совмещая массивные контуры друг с другом. Попытка замены двукратного интегрирования по объему двукратным интегрированием по тонкому контуру приводит в этом случае к появлению несобственного интеграла ввиду того, что расстояния между элементами контура могут обращаться в ноль.
|
|
Разделим потокосцепление контура на внешнее и внутреннее, предполагая, что ток протекает по оси контура (рис. 9–5).
dl 1
r dl 2
Рисунок 9–5
Внешнее потокосцепление равно внешнему потоку и определяется интегралом по контуру l2:
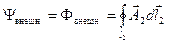, учитывая, что 
,
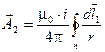запишем окончательно: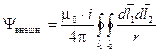 
.
Внутреннее потокосцепление тонкого контура можно принять равным внутреннему потокосцеплению спрямленного проводника такой же длины, выражение для которого мы получили, рассматривая коаксиальный кабель:
.
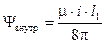Индуктивность тонкого контура определяется его суммарным потокосцеплением:
.
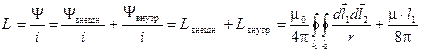В двух последних соотношениях предполагается, что магнитная проницаемость проводника может отличаться от m0.