Теория воспроизведения единиц физических величин
Задача 1
Определить электрическую емкость и заряд кабеля, радиус центральной жилы которого равенr =1,5 см, радиус оболочки R=3,0 см, относительная диэлектрическая проницаемость материала изоляции ε=3,6 а разность потенциалов между центральной жилой и оболочкой 2,5 кВ.
Решение: Емкость кабеля определяем по формуле
,
Где L-длина кабеля, R - радиус оболочки, r -радиус центральной жилы, 
-диэлектрическая проницаемость материала изоляции, 
-электрическая постоянная(абсолютная диэлектрическая проницаемость вакуума).
Переведем данные задачи в единицы СИ: 
Подсчитаем емкость единицы длины кабеля
Найдем теперь заряд, приходящийся также на единицу длины кабеля. Для этого воспользуемся формулой 
,откуда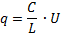 
,
где q -электрический заряд, приходящийся на единицу длины кабеля;U -разность потенциа-лов между центральной жилой и оболочкой, которая в СИ равна 
В.
Подставляем значения: 
Задача 2.
Найти относительную магнитную проницаемость железного сердечникасоленоида, если площадь поперечного сечения последнего 12 
; число витков на каждый метр длины n =400 
;ток, проходящий через соленоид 6 А; магнитный поток, пронизывающий соленоид с сердечником 
Вб.
Решение:Относительная магнитная проницаемость сердечника определяем по формуле
, (*)
где 
-магнитная постоянная в единицах СИ 
Н-напряженность магнитного поля внутри соленоида 
Из формулы(*) находим
Переведем данные задачи в единицы СИ: 
Подставляем: 
Пример обработки ряда прямых измерений
Задача
При измерении напряжения источника питания получены следующие результаты, В: 9,78; 9,65; 9,83; 9,69; 9,74; 9,80; 9,68: 9,71; 9,81. Найти результат и погрешность измерения напряжения и записать в стандартной форме, если систематическая погрешность отсутствует, а случайная распределена по нормальному закону.
Решение:
1.Находят среднее арифметическое и принимают его за результат измерения: 
2. Определяют СКО погрешности результата измерения: 
3. Определяют доверительный интервал погрешности измерения. Поскольку в рассматриваемой задаче число измерений n <20, то доверительный интервал определяется коэффициентом Стьюдента t(n,p). Задавшись вероятностью 0,95 (n =9},по табл1 находим значение коэффициента Стьюдента: t= 2,306. Границы доверительного интервала: D = ± tsx =0,0215.2,306=0,0496»0,05 В.
Записывают результат измерения согласно первой формеГОСТ 8.011-72:
9,74 В; от -0,05 до 0,05 В; Р = 0,95.
Обработка результатов косвенных измерений
При косвенных измерениях, когда измеряется не сама величина непосредственно, а другие величины, связанные определенной зависимостью с величиной, подлежащей измерению, погрешность результата зависит от погрешностей каждого из прямых измерений, входящих в косвенное измерение.
Предположим, что следует определить величину У прямыми измерениями других величин x1, x2 ….., x, с которыми она связана зависимостью y = f(x1,x2….,xm). Пусть для каждой из величин xi известен результат, систематическая погрешность Dci, CKO случайной погрешности s xi. Требуется найти результат и оценить погрешность определения.
Задача решается следующим образом.
1. Значение величины y находят, подставляя в зависимость y=f(x1, x2,…, xm) известные значения xi.
2. Систематическую погрешность измерения У определяют по формуле 
,
где частные производные 
вычисляют при 
.
3. СКО случайной погрешности для y находят по выражению: 
,
где rij - коэффициент корреляции между i -й и j -й погрешностями.
Если погрешности коррелированы ri = ± 1, выражение для sy примет вид: 
При независимых погрешностях rij =0, и выражение для СКО можно записать как: 
Задача. Определить результат и погрешность косвенного измерения мощности по результатам прямых измерений тока и сопротивления с независимыми случайными погрешностями, распределенными по нормальному закону: I =(15,0±0,02) А; P =0,99; R =(10,0±0,8) Ом; P =0,9.
Результат записать в стандартной форме для P = 0,96.
Решение:
1. Определяют результат косвенного измерения мощности по формуле Р = I2R = 5,02*10,0 = 250 Вт.
2. Определяют СКО случайной погрешности косвенного измерения. Для этого сначала находят СКО погрешности прямых измерений I и R. 
, где DI = 0,01 А - половина доверительного интервала случайной погрешности измерения тока, ZI - значение аргумента Z для функции Лапласа F(Z) при 
3. По табл. 2 для F(Z) = 0,495 находят, что ZI = 2,58. Отсюда sI = 0,01/2,58 = 0,0039 А.
Аналогично для нахождения sR определяют 
. По табл. 2 для F(Z) = 0,45 находят ZR = 1,65 и sR=DR/ZR =0,8/1,65 = 0,485 Ом.
Вычисляют частные производные: 
Окончательно определяют СКО косвенного измерения: 
4. Определяют доверительный интервал для погрешности косвенного измерения мощности с доверительной вероятностью P= 0,96. Для F(Z) = PP /2=0,96/2 = 0,48 по табл. 3 находят ZP = 2,04 и вычисляют доверительный интервал: 
.
Записывают результат в стандартной форме: Р =250±24,9 Вт, Р =0,96..
ПРИДЛОЖЕНИЕ
Коэффициент t можно определить из таблицы 1 по заданному числу наблюдений n и заданной /выбранной/ доверительной вероятности P.
Таблица 1
| n | P | ||||||
| 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 0,95 | 0,99 | |
| 1,00 | 1,38 | 2,0 | 3,1 | 6,3 | 12,7 | 63,7 | |
| 0,82 | 1,06 | 1,3 | 1,9 | 2,9 | 4,3 | 9,9 | |
| 0,77 | 0,98 | 1,3 | 1,6 | 2,4 | 3,2 | 5,8 | |
| 0,74 | 0,94 | 1,2 | 1,5 | 2,1 | 2,8 | 4,6 | |
| 0,73 | 0,92 | 1,2 | 1,5 | 2,0 | 2,6 | 4,0 | |
| 0,72 | 0,90 | 1,1 | 1,4 | 1,9 | 2,4 | 3,7 | |
| 0,71 | 0,90 | 1,1 | 1,4 | 1,9 | 2,4 | 3,5 | |
| 0,71 | 0,90 | 1,1 | 1,4 | 1,9 | 2,3 | 3,4 | |
| 0,70 | 0,88 | 1,1 | 1,4 | 1,8 | 2,3 | 3,3 | |
| 0,70 | 0,87 | 1,1 | 1,4 | 1,8 | 2,2 | 3,1 | |
| 0,69 | 0,87 | 1,1 | 1,4 | 1,8 | 2,2 | 3,0 | |
| 0,69 | 0,87 | 1,1 | 1,3 | 1,8 | 2,1 | 2,9 | |
| 0,69 | 0,86 | 1,1 | 1,3 | 1,7 | 2,1 | 2,9 | |
| 0,69 | 0,86 | 1,1 | 1,3 | 1,7 | 2,1 | 2,9 |
При нормальном законе распределения погрешностей границы доверительного интервала определяются функцией Лапласа: 
,
где Ф(z) - нормированная функция Лапласа: 
Значения Ф(z) - взяты из таблицы 2.
Таблица 2
| Z | Ф(z) | Z | Ф(z) |
| 0,0 | 0,00000 | 2,1 | 0,48214 |
| 0,1 | 0,03983 | 2,2 | 0,48610 |
| 0,2 | 0,77926 | 2,3 | 0,48928 |
| 0,3 | 0,11791 | 2,4 | 0,49180 |
| 0,4 | 0,15542 | 2,5 | 0,49379 |
| 0,5 | 0,19146 | 2,6 | 0,49534 |
| 0,6 | 0,22575 | 2,7 | 0,49653 |
| 0,7 | 0,25804 | 2,8 | 0,49744 |
| 0,8 | 0,28814 | 2,9 | 0,49813 |
| 0,9 | 0.31594 | 3,0 | 0,49865 |
| 1,0 | 0,34131 | 3,1 | 0,49903 |
| 1,1 | 0,36433 | 3,2 | 0,49931 |
| 1,2 | 0,38493 | 3,3 | 0,49952 |
| 1,3 | 0,40320 | 3,4 | 0,49966 |
| 1,4 | 0,41924 | 3.5 | 0,49977 |
| 1,5 | 0,43319 | 3,6 | 0,49984 |
| 1,6 | 0,44520 | 3,7 | 0,49989 |
| 1,7 | 0,45543 | 3,8 | 0,49993 |
| 1,8 | 0,46407 | 3,9 | 0,49995 |
| 1,9 | 0,47128 | 4,0 | 0,499968 |
| 2,0 | 0,47725 | 4,5 | 0,499999 |