Вариант 4
Задание 1.1. Построить математическую модель механической системы, состоящей из пружины с жёсткостью k, один конец которой жёстко закреплен, а на другом находится тело массой m. Тело скользит по горизонтальному стержню: коэффициент вязкого сопротивления μ. Смещение тела из положения равновесия равно x 0.
Найти:
а) амплитуду, частоту и период свободных колебаний механической системы;
б) частоту и период затухающих колебаний системы;
в) уравнение огибающей кривой колебаний;
г) смещение, скорость и ускорение тела в момент времени 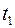 для затухающих колебаний.
для затухающих колебаний.
Построить графики смещения свободных и затухающих колебаний системы в зависимости от времени.
Дано:
k = 100 Н/м; m = 0,9 кг; 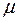 = 0,6; x0 = 0,10 м; t1 = 3,5 с.
= 0,6; x0 = 0,10 м; t1 = 3,5 с.
Решение:

Рис.1.1
Система состоит из пружины и груза, скользящего по горизонтальному стержню:
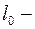 длина пружины до деформации;
длина пружины до деформации;
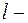 длина деформированной пружины;
длина деформированной пружины;
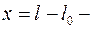 абсолютная деформация пружины или величина отклонения тела от положения равновесия.
абсолютная деформация пружины или величина отклонения тела от положения равновесия.
Рассмотрим силы, действующие на колеблющееся тело:
1) Во-первых, это сила упругости пружины, которая всегда пытается вернуть пружину в положение равновесия и для малых деформаций вычисляется по закону Гука:

Сила упругости пропорциональна величине отклонения тела от положения равновесия 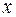 и коэффициенту жёсткости пружины
и коэффициенту жёсткости пружины  .
.
Физический смысл 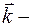 сила, необходимая для деформации пружины на 1 единицу длины.
сила, необходимая для деформации пружины на 1 единицу длины.
Знак “–“ показывает, что сила 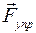 направлена в сторону, противоположную направлению отклонения.
направлена в сторону, противоположную направлению отклонения.
2) Во-вторых, это – сила вязкого трения, которая для малых скоростей движения пропорциональна коэффициенту вязкого сопротивления 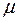 и величине скорости
и величине скорости  :
:
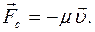
Физический смысл коэффициента вязкого сопротивления равен силе, возникающей при движении тела.
Знак “–“ показывает, что эта сила направлена в сторону, противоположную вектору скорости движения тела.
Введем систему координат с началом в точке О: ось 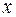 направим горизонтально вправо, ось
направим горизонтально вправо, ось 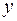 - вертикально вниз.
- вертикально вниз.
Предположим, что в текущий момент времени  координата скорости и ускорения тела положительны. По второму закону Ньютона:
координата скорости и ускорения тела положительны. По второму закону Ньютона:


где  реакция опоры;
реакция опоры;  сила тяжести груза,
сила тяжести груза,
тогда
 математическая модель в векторной форме.
математическая модель в векторной форме.
Запишем проекции
на ось 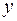 :
:
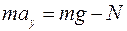 , так как движение вдоль оси
, так как движение вдоль оси 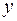 отсутствует, то
отсутствует, то
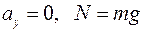 ;
;
на ось 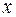 :
:
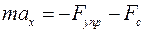 ,
,  (*)
(*)
Обозначим через  величину отклонения тела от положения равновесия в произвольный момент времени
величину отклонения тела от положения равновесия в произвольный момент времени  .
.
Выразим через 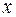 ускорение и скорость:
ускорение и скорость:
 . (**)
. (**)
Подставив (**) в уравнение (*), получим:
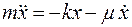 . (1)
. (1)
Добавим начальные условия:
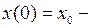 начальное смещение,
начальное смещение,
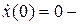 начальная скорость.
начальная скорость.
Таким образом, мы построили математическую модель рассматриваемой системы в виде задачи Коши для ОДУ 2го порядка.

Преобразуем уравнение (1), перенесём все слагаемые в левую часть и разделим на 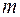 :
:

Введём обозначения:
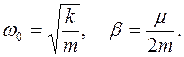
Получим уравнение:
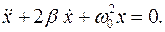 (2)
(2)
Решаем уравнение (2) для начальных условий задачи:
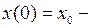 начальное смещение, (3)
начальное смещение, (3)
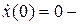 начальная скорость. (4)
начальная скорость. (4)
При отсутствии сопротивления среды 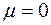 уравнение (2) принимает вид:
уравнение (2) принимает вид:
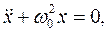 (5)
(5)
которое описывает свободные колебания механической системы.
а) Решая дифференциальное уравнение (5) с условиями (3), (4) в системе Maxima [2], получим:
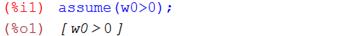
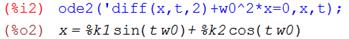
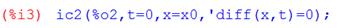
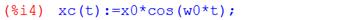
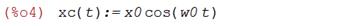
Откуда следует, что решение задачи (5), (3), (4) имеет вид:
 (6)
(6)
Выражение (6) представляет собой гармонические колебания (синусоидальную зависимость) с круговой частотой  и амплитудой
и амплитудой 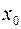 . Подставляя числовые значения исходных данных, получим:
. Подставляя числовые значения исходных данных, получим:
– амплитуда свободных колебаний механической системы 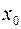 =0,10 м;
=0,10 м;
– частота свободных колебаний механической системы:


 ;
;
– период свободных колебаний механической системы:



График смещений свободных колебаний системы  представлен на Рис.1.2.
представлен на Рис.1.2.
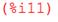

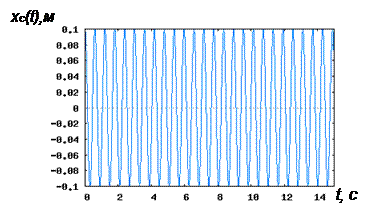
Рис.1.2
б) Решая дифференциальное уравнение (2) с условиями (3), (4) в системе Maxima, получим:


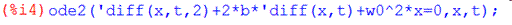

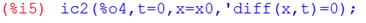
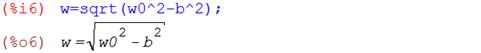
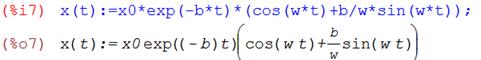
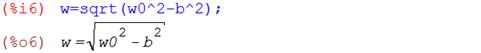
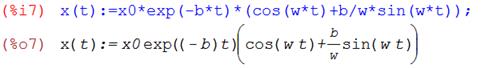
Откуда следует, что решение задачи (2), (3), (4) имеет вид:
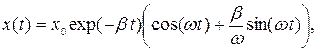 (7) где
(7) где 
– Частота затухающих колебаний системы:



– Период затухающих колебаний механической системы:
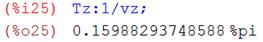

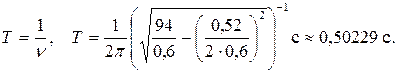
в) Множитель 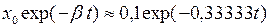 в выражении (7) представляет собой огибающую кривой колебаний.
в выражении (7) представляет собой огибающую кривой колебаний.
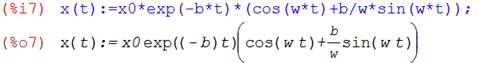

Уравнение огибающей кривой колебаний:
x1=0,1e-0,33333t.
г) Смещение, скорость и ускорение тела в момент времени  = 3,5 с для затухающих колебаний получим по выражению (7) в Maxima, выполняя дифференцирование выражения (7) (для скорости и ускорения) и подставляя числовые значения параметров:
= 3,5 с для затухающих колебаний получим по выражению (7) в Maxima, выполняя дифференцирование выражения (7) (для скорости и ускорения) и подставляя числовые значения параметров:
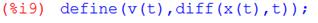
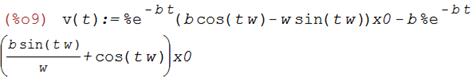
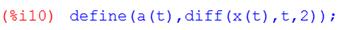



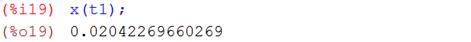

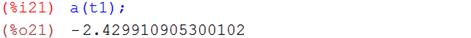
Смещение, скорость и ускорение тела в момент времени 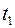 = 3,5 с для затухающих колебаний соответственно равны:
= 3,5 с для затухающих колебаний соответственно равны:
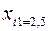 ≈ 0,02042 м;
≈ 0,02042 м; 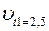 ≈ 0,24108 м/с;
≈ 0,24108 м/с; 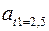 ≈-2,42991 м/с2.
≈-2,42991 м/с2.
График смещений затухающих колебаний системы x(t) представлен на Рис.1.3.
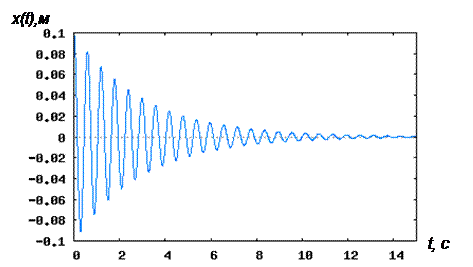
Рис.1.3
График скорости затухающих колебаний системы  изображен на Рис.1.4.
изображен на Рис.1.4.


Рис.1.4
График ускорения затухающих колебаний системы a(t) показан на Рис.1.5.
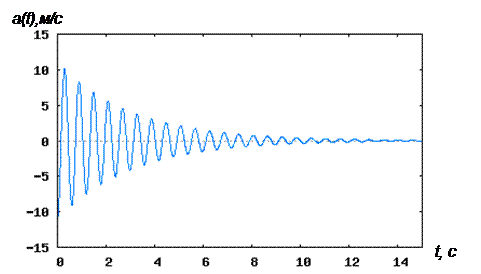
Рис.1.5
Графики смещения, скорости и ускорения затухающих колебаний системы: x(t), 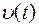 , a(t), - при
, a(t), - при  представлены на Рис.1.6.
представлены на Рис.1.6.

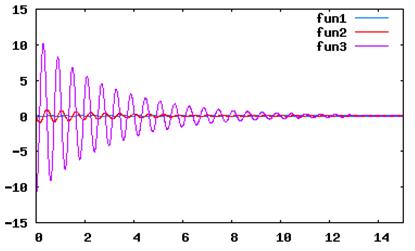
Рис.1.6
Ответ:
а) 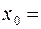 0,10 м;
0,10 м;  1,67764Гц;
1,67764Гц;  0,59608 с;
0,59608 с;
б) 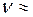 1,990891Гц;
1,990891Гц;  0,50229 с;
0,50229 с;
в) 0,1e-0,33333t;
г) 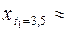 0,02042 м;
0,02042 м;  0,24108 м/с;
0,24108 м/с;  -2,42991 м/с2.
-2,42991 м/с2.
Задание 1.2. Построить математическую модель всплытия подводной лодки. Пусть лодка водоизмещением W движется горизонтально со скоростью υ на глубине H от поверхности моря. Средняя плотность лодки ρ1. В момент t0 лодка начинает всплытие. Сопротивлением воды можно пренебречь.
Определить:
1) время t 1, когда лодка всплывет на поверхность моря;
2) расстояние L, которое пройдет лодка в горизонтальном направлении до момента всплытия;
3) вертикальную скорость u лодки;
4) траекторию движения подводной лодки в координатах (l, h);
5) тип соответствующей кривой.
Плотность воды принять равной ρ0 = 10-3 кг/м3. Сделать чертеж.
Дано:
W = 1360 т, υ = 18 км/ч, Н = 280 м, ρ 1 = 0,7∙10-3 кг/м3
Решение:
Для численных расчетов переводим исходные данные в СИ:
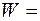 1,36∙106 кг;
1,36∙106 кг; 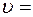 18∙1000/3600 м/с = 5 м/с.
18∙1000/3600 м/с = 5 м/с.
Модель должна позволять:
– вычислять положение лодки в любой момент времени всплытия;
– определять дальность расстояния от начала всплытия до конца всплытия;
– скорость в момент всплытия, траекторию движения;
Исходные данные:
По закону Архимеда на тело, погруженное в жидкость, действует выталкивающая сила, равная весу жидкости в объеме тела.
Горизонтальная скорость 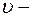 скорость подводной лодки в начале всплытия.
скорость подводной лодки в начале всплытия.
Глубина начала всплытия Н.
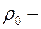 плотность воды;
плотность воды;  средняя плотность лодки.
средняя плотность лодки.
Примем следующие гипотезы:
– Объектом моделирования является подводная лодка, которую будем считать точкой массы m, сосредоточенной в центре масс.
– Движение происходит в поле сил тяжести.
– При малых скоростях силами сопротивления можно пренебречь: скорость подводной лодки примерно 1/10 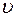 .
.
– Плотность воды не меняется в процессе всплытия в зависимости от температуры воды, тогда сила Архимеда будет величиной постоянной.
– 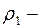 средняя плотность лодки, не содержащей балластной воды.
средняя плотность лодки, не содержащей балластной воды.
– Всплытие происходит в вертикальной плоскости, проходящей через вектор начальной скорости при отсутствии боковых течений и вертикальных течений.
Математическая постановка задачи

Рис.2.1
Используем второй закон Ньютона, если на тело массой m действует сила 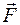 , то оно движется в направлении действия силы с ускорением
, то оно движется в направлении действия силы с ускорением 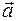 , пропорциональным силе и обратно пропорциональным массе тела, т.е.
, пропорциональным силе и обратно пропорциональным массе тела, т.е.
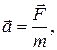
где 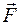 - главный вектор сил, действующих на тело.
- главный вектор сил, действующих на тело.

тогда получим математическую модель в векторной форме:
 (1)
(1)
Для перехода к скалярной форме составим проекции уравнения (1) на оси выбранных координат. Начало движения возьмем в точке О.
Обозначим через 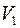 объем подводной лодки в м3. Тогда
объем подводной лодки в м3. Тогда 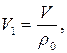
где 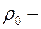 плотность воды.
плотность воды.
Масса подводной лодки во время всплытия может быть определена произведением:
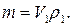
На подводную лодку вертикально вверх действует выталкивающая сила Архимеда:

где 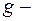 ускорение свободного падения.
ускорение свободного падения.
Также в вертикальном направлении – но уже вниз – на лодку действует сила тяжести (вес лодки):
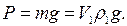
Положительная разность сил 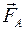 и
и 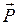 обеспечивает подъём лодки в вертикальном направлении
обеспечивает подъём лодки в вертикальном направлении 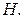
Уравнение движения лодки может быть записано в виде:
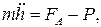 (1)
(1)
где 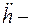 ускорение движения лодки в вертикальном направлении (отсчитывается от поверхности моря вглубь моря). То, что
ускорение движения лодки в вертикальном направлении (отсчитывается от поверхности моря вглубь моря). То, что 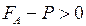 показывает, что лодка должна всплывать.
показывает, что лодка должна всплывать.
Перенесём отсчёт времени на момент начала всплытия и запишем задачу Коши для уравнения (1) в виде:
 . (2)
. (2)
Разделив обе части на  , получим:
, получим:
 (3)
(3)
 (4) (вертикальная скорость в начальный момент равна нулю).
(4) (вертикальная скорость в начальный момент равна нулю).
Таким образом, мы построили математическую модель рассматриваемой системы в виде задачи Коши для ОДУ 2го порядка.
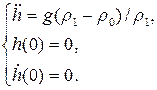
Решим задачу (3) с учётом (4) в программе Maxima [2]:
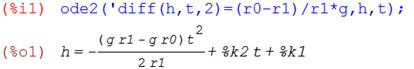
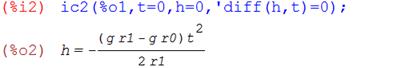

Откуда, следует, что выражение глубины погружения в зависимости от времени имеет вид:
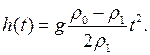 (4)
(4)
1) Момент времени, когда лодка всплывет на поверхность моря, определим по значению 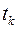 из выражения (5) при котором
из выражения (5) при котором 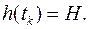 Решая уравнение,
Решая уравнение,

получим:
 (5)
(5)
Подставляя числовые значения параметров в (5), получим:
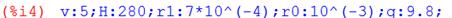


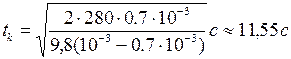 .
.
Таким образом, 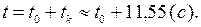
2) Координата l, характеризующая горизонтальное положение подлодки, изменяется по закону движения тела с постоянной скоростью:
 (6)
(6)
т.е. по горизонтали  лодка перемещается равномерно со скоростью
лодка перемещается равномерно со скоростью 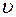 . Следовательно, зависимость от времени можно представить линейной связью:
. Следовательно, зависимость от времени можно представить линейной связью:
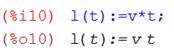
 (7)
(7)
Подставляя в (7) время всплытия, получим расстояние, которое пройдет лодка в горизонтальном направлении от начала до окончания этапа всплытия:


3) Для нахождения вертикальной скорости лодки достаточно продифференцировать по времени t выражение (4):

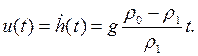 (8)
(8)

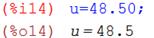
Вертикальная скорость подводной лодки: 
4) На Рис. 2.2 показан график зависимости 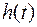 при изменении времени от 0 до 12 с:
при изменении времени от 0 до 12 с:


Рис.2.2
Из уравнения (7) выражаем время:
 (9)
(9)

Подставляя (9) в уравнение (4), находим траекторию движения подводной лодки в координатах (l, h):
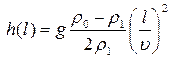 или
или  (10)
(10)
которая представляет собой параболу с вершиной в точке l = 0, h = 0.
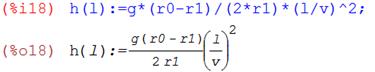

Траектория движения подводной лодки в координатах (l, h) показана на Рис.2.3 в интервале изменения l от 0 до 60.

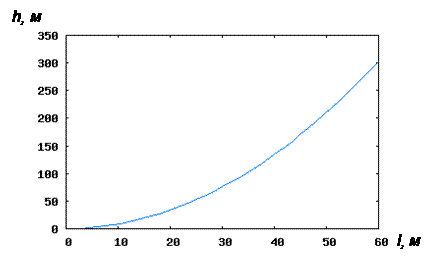
Рис.2.3
5) Подставляя числовые значения параметров в (10), получим:
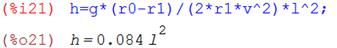

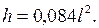 (11)
(11)
Итак, непосредственное применение закона Архимеда, определяющего величину выталкивающей силы, и закона Ньютона, связывающего силу, действующую на тело, и его ускорение, позволило легко найти траекторию движения подводной лодки.
Ответ: 1)  2)
2) 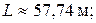 3)
3) 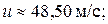 4) Рис.2.3; 5) тип кривой – парабола:
4) Рис.2.3; 5) тип кривой – парабола: 