Наряду с дифференциальной системой
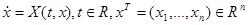

будем рассматривать множество систем


где 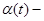 непрерывная скалярная нечётная функция, а
непрерывная скалярная нечётная функция, а 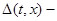 произвольная непрерывно дифференцируемая вектор-функция. Систему
произвольная непрерывно дифференцируемая вектор-функция. Систему  назовём возмущённой, а добавку
назовём возмущённой, а добавку  возмущением. Выясним вопрос об эквивалентности в смысле совпадения отражающих функций дифференциальных систем
возмущением. Выясним вопрос об эквивалентности в смысле совпадения отражающих функций дифференциальных систем  и
и  .
.
Как известно, отражающая функция системы  обязана удовлетворять следующему соотношению
обязана удовлетворять следующему соотношению


Для решения поставленной задачи нам потребуются некоторые вспомогательные утверждения. Справедлива [4]
Лемма 3.1. Для любых трёх вектор-функций

имеет место тождество


Доказательство.
Будем преобразовывать левую часть тождества 
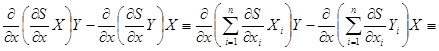




Лемма доказана.
Лемма 3.2. Пусть  есть отражающая функция системы
есть отражающая функция системы  с непрерывно дифференцируемой правой частью. Тогда для каждой непрерывно дифференцируемой вектор-функции
с непрерывно дифференцируемой правой частью. Тогда для каждой непрерывно дифференцируемой вектор-функции  функция
функция


удовлетворяет тождеству


Доказательство.
Подставив функцию  в выражение
в выражение  , придем к следующим тождествам:
, придем к следующим тождествам:

Выразим из соотношения  частную производную
частную производную  , подставим в последнее тождество и будем преобразовывать получившееся выражение:
, подставим в последнее тождество и будем преобразовывать получившееся выражение:

Применив к первым двум слагаемым последней части этой цепочки тождеств тождество 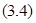 придем к следующим соотношениям:
придем к следующим соотношениям:


Выразим из соотношения  выражение, находящееся в скобках последнего тождества и подставим в последнее из получившихся тождеств:
выражение, находящееся в скобках последнего тождества и подставим в последнее из получившихся тождеств:

Учитывая определение функции  , полученное тождество можно переписать в виде
, полученное тождество можно переписать в виде

Мы пришли к соотношению

Прибавив к левой и правой частям этого соотношения выражение 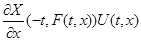 , придем к нужному нам тождеству
, придем к нужному нам тождеству 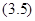 и тем самым докажем лемму.
и тем самым докажем лемму.
Лемма доказана.
Теорема 3.1. Пусть вектор-функция  является решением дифференциального уравнения в частных производных
является решением дифференциального уравнения в частных производных


Тогда возмущенная дифференциальная система  где
где 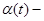 произвольная непрерывная скалярная нечетная функция, эквивалентна дифференциальной системе
произвольная непрерывная скалярная нечетная функция, эквивалентна дифференциальной системе  в смысле совпадения отражающих функций.
в смысле совпадения отражающих функций.
Доказательство. Пусть 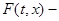 отражающая функция системы
отражающая функция системы  Следовательно, эта функция удовлетворяет дифференциальному уравнению
Следовательно, эта функция удовлетворяет дифференциальному уравнению  . Покажем, что помимо этого уравнения при условиях теоремы она удовлетворяет тождеству
. Покажем, что помимо этого уравнения при условиях теоремы она удовлетворяет тождеству


С этой целью введем функцию  по формуле
по формуле 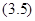 . Согласно предыдущей лемме, эта функция удовлетворяет тождеству
. Согласно предыдущей лемме, эта функция удовлетворяет тождеству  . При условиях доказываемой теоремы, с учетом соотношения
. При условиях доказываемой теоремы, с учетом соотношения 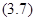 это тождество переписывается в виде
это тождество переписывается в виде

Кроме того, поскольку для всякой отражающей функции  верно тождество
верно тождество  , имеют место соотношения
, имеют место соотношения

Поставим следующую задачу Коши для функции  :
:
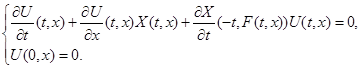
Решение этой задачи существует и единственно [6, с.66]. Таким образом, имеет место тождество  влекущее за собой тождество
влекущее за собой тождество  .
.
Теперь покажем, что отражающая функция  дифференциальной системы
дифференциальной системы  является также и отражающей функцией дифференциальной системы
является также и отражающей функцией дифференциальной системы  . Для этого нужно проверить выполнение основного соотношения
. Для этого нужно проверить выполнение основного соотношения  , которое в данном случае должно быть переписано в виде
, которое в данном случае должно быть переписано в виде


Последовательно преобразовывая левую часть последнего соотношения и учитывая нечетность функции  , приходим к следующей цепочке тождеств:
, приходим к следующей цепочке тождеств:


Оба слагаемых, стоящих в квадратных скобках, тождественно равны нулю. Первое - потому, что для отражающей функции системы  верно тождество
верно тождество  , второе - потому, что при условиях теоремы верно тождество
, второе - потому, что при условиях теоремы верно тождество  . Следовательно, тождество
. Следовательно, тождество  выполняется и функция
выполняется и функция  является отражающей функцией системы
является отражающей функцией системы  .
.
Теорема доказана.
Следствие3.1. Пусть функции  являются решениями дифференциального уравнения в частных производных
являются решениями дифференциального уравнения в частных производных  . Тогда все дифференциальные системы вида
. Тогда все дифференциальные системы вида


где  нечетные скалярные непрерывные функции, такие, что ряд
нечетные скалярные непрерывные функции, такие, что ряд  сходится к непрерывно дифференцируемой функции, эквивалентны между собой в смысле совпадения отражающих функций и все они эквивалентны дифференциальной системе
сходится к непрерывно дифференцируемой функции, эквивалентны между собой в смысле совпадения отражающих функций и все они эквивалентны дифференциальной системе  .
.
Доказательствоследствия очевидно и сводится к последовательному применению теоремы 3.1
Замечание 3.1. В [2, с.24] доказано, что правая часть стационарной дифференциальной системы, эквивалентной дифференциальнойсистеме  в смысле совпадения отражающих функций, если такая система существует, может быть найдена по формуле
в смысле совпадения отражающих функций, если такая система существует, может быть найдена по формуле  Учитывая этот факт и сформулированное выше следствие, для нас важно установить, когда вектор-функция
Учитывая этот факт и сформулированное выше следствие, для нас важно установить, когда вектор-функция 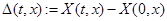 может быть представлена в виде
может быть представлена в виде


где  решения уравнения
решения уравнения  . Последующие рассмотрения направлены на решение этой задачи. Решив ее, мы сможем заменить изучение свойств решений нестационарных систем изучением свойств решений стационарных систем вида
. Последующие рассмотрения направлены на решение этой задачи. Решив ее, мы сможем заменить изучение свойств решений нестационарных систем изучением свойств решений стационарных систем вида  или, если угодно, использовать уже изученные стационарные системы для изучения нестационарных систем.
или, если угодно, использовать уже изученные стационарные системы для изучения нестационарных систем.
Стационарный интеграл
Рассмотрим систему
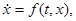
 ,
, 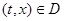

с непрерывной в области  функцией
функцией 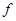 .
.
Дифференцируемая функция  , заданная в некоторой подобласти
, заданная в некоторой подобласти  области
области  , называется первым интегралом системы
, называется первым интегралом системы  в области
в области  , если для любого решения
, если для любого решения  ,
, 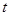
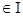 , системы
, системы  , график которого расположен в
, график которого расположен в  функция
функция  ,
, 
 , постоянна, т.е.
, постоянна, т.е.  зависит только от выбора решения
зависит только от выбора решения  и не зависит от
и не зависит от  .
.
Пусть 
 , есть некоторая функция. Производной от функции
, есть некоторая функция. Производной от функции  в силу системы
в силу системы  назовем функцию
назовем функцию 
 , определяемую равенством
, определяемую равенством

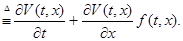
Лемма 4.1. Для любого решения  ,
, 
 , системы
, системы  , график которого расположен в
, график которого расположен в  , имеет место тождество
, имеет место тождество



 .
.
Доказательство. Действительно,

Лемма 4.2. Дифференцируемая функция  ,
,  представляет собой первый интеграл системы
представляет собой первый интеграл системы  тогда и только тогда, когда производная
тогда и только тогда, когда производная  в силу системы
в силу системы  тождественно в
тождественно в 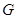 обращается в нуль.
обращается в нуль.
Необходимость. Пусть  есть первый интеграл системы
есть первый интеграл системы  . Тогда для любого решения
. Тогда для любого решения  этой системы, применяя лемму 1 будем иметь тождества
этой системы, применяя лемму 1 будем иметь тождества

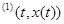


откуда при  получим равенство
получим равенство 
 справедливое при всех значениях
справедливое при всех значениях  и
и  . Необходимость доказана.
. Необходимость доказана.
Достаточность. Пусть теперь  при всех
при всех  Тогда для любого решения
Тогда для любого решения  системы
системы  на основании леммы1 будем иметь тождество
на основании леммы1 будем иметь тождество

а с ним и достаточность.
Лемма доказана.
Из определения первого интеграла следует, что постоянная на  функция также является первым интегралом системы
функция также является первым интегралом системы  . Первый интеграл
. Первый интеграл  будем называть невырожденным на
будем называть невырожденным на  , если при всех
, если при всех 
 выполняется неравенство
выполняется неравенство

Функцию 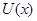 будем называть стационарным первым интегралом системы
будем называть стационарным первым интегралом системы  , если она не зависит от
, если она не зависит от 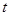 и является первым интегралом системы
и является первым интегралом системы 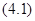 .
.
Теорема 4.1. Для того, чтобы система  с
с  раз дифференцируемой по
раз дифференцируемой по 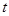 правой частью имела в
правой частью имела в  невырожденный стационарный первый интеграл, необходимо выполнение тождества
невырожденный стационарный первый интеграл, необходимо выполнение тождества



где  ,
,  компоненты вектор-функции
компоненты вектор-функции 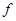 .
.
Доказательство. Пусть  стационарный первый интеграл системы
стационарный первый интеграл системы  . Тогда согласно лемме 4.2 должно выполняться тождество
. Тогда согласно лемме 4.2 должно выполняться тождество


Это означает, что при каждом фиксированном  функции
функции 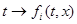 линейно зависимы на интервале их существования. Поэтому вронскиан этих функций (левая часть тождества
линейно зависимы на интервале их существования. Поэтому вронскиан этих функций (левая часть тождества  ) обязан обращаться в нуль.
) обязан обращаться в нуль.
Теорема доказана.
Выясним условия, при которых система  имеет стационарный интеграл. Будем считать, что условия теоремы 4.1 выполнены. Составим систему линейных уравнений относительно неизвестных функций
имеет стационарный интеграл. Будем считать, что условия теоремы 4.1 выполнены. Составим систему линейных уравнений относительно неизвестных функций 

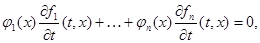
…………………………………………. 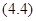

Теорема 4.2. Для того, чтобы система  с
с  раз дифференцируемой по
раз дифференцируемой по 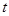 правой частью имела хотя бы один стационарный интеграл
правой частью имела хотя бы один стационарный интеграл  , необходимо и достаточно существование такого независящего от
, необходимо и достаточно существование такого независящего от  решения
решения 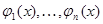 системы
системы 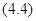 , для которого уравнение Пфаффа
, для которого уравнение Пфаффа

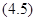
интегрируется одним соотношением  .
.
Необходимость. Пусть система  имеет стационарный интеграл
имеет стационарный интеграл  . Тогда согласно лемме 4.2 должно выполняться тождество
. Тогда согласно лемме 4.2 должно выполняться тождество  . Дифференцируя тождество
. Дифференцируя тождество 
 раз по
раз по  , убеждаемся в том, что совокупность функций
, убеждаемся в том, что совокупность функций  решение системы
решение системы 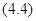 .
.
Достаточность. Пусть теперь система 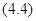 имеет не зависящее от
имеет не зависящее от  решение, для которого уравнение Пфаффа
решение, для которого уравнение Пфаффа 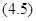 интегрируется одним соотношением
интегрируется одним соотношением  . Тогда существует [6] такая функция
. Тогда существует [6] такая функция  , для которой
, для которой


Поэтому

так как 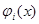 удовлетворяет первому уравнению системы
удовлетворяет первому уравнению системы 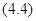 . Из тождества
. Из тождества  следует достаточность.
следует достаточность.
Теорема доказана.
Теорема 4.3. Пусть система  имеет
имеет 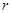 линейно независимых при каждом
линейно независимых при каждом  решений
решений
 ,
,  ,
,
для которых соответствующие уравнения Пфаффа


интегрируется с помощью соотношений 
 .
.
Тогда 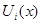 представляют собой
представляют собой  независимых стационарных интегралов системы
независимых стационарных интегралов системы  .
.
Доказательство. Согласно теореме 4.2 функции 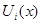 являются первыми интегралами системы
являются первыми интегралами системы  . Покажем, что они независимы. Отметим, что для каждой функции
. Покажем, что они независимы. Отметим, что для каждой функции 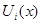 существует функция
существует функция  , для которой
, для которой



Поэтому матрица Якоби 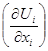 имеет вид
имеет вид

Из линейной независимости векторов  ,
,  при каждом
при каждом  следует, что при всех
следует, что при всех  ранг матрицы Якоби равен
ранг матрицы Якоби равен  . Поэтому функции
. Поэтому функции  ,
,  , являются независимыми [7, c.682].
, являются независимыми [7, c.682].
Теорема доказана.
Теорема 4.4. Пусть выполнены все условия теоремы 4.1 и существует некоторое  при котором уравнение Пфаффа
при котором уравнение Пфаффа

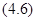
не вырождается в тождество и интегрируется одним соотношением  . Тогда функция
. Тогда функция  является независимым стационарным первым интегралом системы
является независимым стационарным первым интегралом системы  . Всякий другой стационарный первый интеграл зависит от
. Всякий другой стационарный первый интеграл зависит от  .
.
Доказательство. Так как уравнение 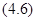 не вырождается в тождество, то для функций
не вырождается в тождество, то для функций 
 , переменного
, переменного  при фиксированном
при фиксированном  выполнены все условия примечания к теореме 1 §1 [2, с 13]. На основании этого примечания функции
выполнены все условия примечания к теореме 1 §1 [2, с 13]. На основании этого примечания функции  линейно зависимы. Соответствующие коэффициенты
линейно зависимы. Соответствующие коэффициенты  могут быть найдены путём разложения по элементам первой строки определителя
могут быть найдены путём разложения по элементам первой строки определителя

Эти коэффициенты образуют единственное с точностью до множителя решение  системы
системы 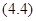 , которому соответствует уравнение Пфаффа вида
, которому соответствует уравнение Пфаффа вида  . Ссылка на теорему 4.3 завершит доказательство.
. Ссылка на теорему 4.3 завершит доказательство.