Рассмотрим систему
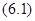
Лемма 6.1. Пусть 
периодическая дифференциальная система 
с решением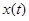 
и отражающей функцией 
эквивалентна в смысле совпадения отражающих функций некоторой дифференциальной системе с решением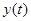 
и отражающей функцией 
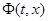, причём имеет место равенство 
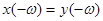, а 
и 
продолжимы на 
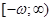. Тогда для любого натурального 
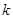имеет место равенство
Теорема 6.1. Пусть 
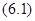периодическая дифференциальная система с решением эквивалентна в смысле совпадения отражающих функций стационарной системе
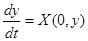
с решением 
. И пусть выполняются следующие условия:
А) верно равенство
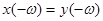
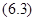
Б) ограничено на 
;
В) существует число 
, такое, что неравенство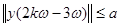 
выполняется для всякого натурального ;
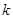Г) все решения 
системы 
, для которых верно неравенство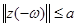 
, продолжимы на 
.
Тогда продолжимо и ограничено на .
Доказательство. Докажем сначала продолжимость решения на 
. Это решение продолжимо на , что следует из условия Г), равенства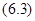 
и условия Б) (при 
): 
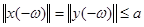. Покажем, что решение продолжимо и на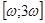 
. Заметим, что функция 
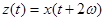является решением системы 
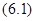и для него выполняются соотношения 
, справедливость которых следует из основного свойства отражающей функции. Тогда по условию теоремы продолжимо на , т.е. действительно продолжимо на 
. Индукцией по 
доказывается, что 
продолжимо на 
. В силу произвольности отсюда следует продолжимость на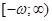 
.
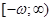Теперь докажем, что ограничено на . Из продолжимости на 
тех решений 
системы 
, для которых выполняется неравенство 
, следует существование числа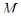 
, для которых выполняется неравенство 
для любого 
из . Из леммы 6.1 вытекает, что 
для любого натурального . Поэтому для 
справедливы соотношения 
, и, значит, в свою очередь, имеют место соотношения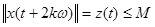 
при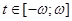 
.
Таким образом, для любого натурального имеет место неравенство, обозначающее ограниченность решения на .
Теорема доказана.
Теорема 6.2. Пусть выполнены условия А), В), и Г) теоремы 6.1, а решение 
системы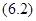 
является 
периодическим и асимптотически устойчивым (асимптотически неустойчивым). Тогда решение системы 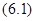также 
периодично и асимптотически устойчиво (асимптотически неустойчиво).
Доказательство. Пусть решение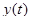 
является периодическим. Тогда верны равенства
,
т.е. 
. Это означает, что 
является неподвижной точкой отображения за период . Откуда и следует периодичность решения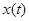 
.
Дальнейшее доказательство следует из факта совпадения отображени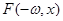й 
и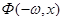 
за период для двух рассматриваемых систем.
Теорема доказана.
Заключение
При изучении поставленных вопросов важную роль играет отображение за период (отображение Пуанкаре), для отыскание которого используют вспомогательные функции, названные отображающими функциями.
Отражающей функцией названа функция, позволяющая по состоянию системы x (t) в момент времени t найти состояние этой системы x (-t) в момент времени (-t). Эта функция применена для качественного исследования неавтономных систем и, в частности, для решения вопросов существования и устойчивости периодических дифференциальных систем.
Знание отражающей функции позволяет определить отображение за период системы и, значит, найти начальные данные её периодических решений, а также проверить их на устойчивость.
Основное соотношение
позволяет найти отражающую функцию или установить её структуру. Даны необходимые и достаточные условия, того, чтобы первая компонента отражающей функции дифференциальной системы второго порядка не зависела от второй компоненты.
Частным случаем этого результата являются необходимые и достаточные условия чётности первой компоненты любого решения рассматриваемой системы. Установлен вид отражающей функции при указанном условии.