ВВЕДЕНИЕ
Актуальность. На данный момент в сфере образования происходит активное внедрение новых решений и технологий. Всё больше усилий прилагается для автоматизации процессов сдачи нормативов, проверки работ выполненных обучающимися. С этой целью вводятся различного рода системы хранения и обработки данных, виртуальные среды дистанционного обучения и контроля.
Однако у ряда подобных систем имеется существенный недостаток. Ввиду того, что система не различает людей по каким-либо факторам, процессы тестирования проверяют всех одинаково, что несет за собой ухудшение общего КПД системы, перерасход времени использования оборудования, вследствие чего замедляется сам процесс аттестации.
В данном случае помочь справиться с негативными факторами может применение теории систем массового обслуживания. Грамотное распределение очередей заявок по обслуживающим устройствам с учётом свойств той или иной заявки, с правильным распределением времени обслуживания, может сократить, как общее количество времени на обслуживание потока заявок, так и повысить качество проведение аттестации.
Разработка программных имитационных моделей различных процессов – активно разрабатываемая на данный момент тема исследований, однако стоит отметить, что число работ посвященных разработке имитационных моделей так или иначе связанных с образовательными процессами очень мало, что позволяет говорить о высокой научной значимости данного исследования.
А с учётом возможности внедрения подобной технологии в информационные системы образовательных учреждений, разработка подобного рода программного обеспечения является актуальной на сегодняшний день задачей.
Объект исследования: процесс прохождения студентами тестирования в высших учебных, либо иных учебных заведениях.
Предмет исследования: имитационные модели образовательного процесса.
Цель работы заключалась в разработке программной модели информационной системы образовательного процесса.
Основные задачи исследования:
• Анализ литературных данных о существующих подходах к моделированию сложных систем;
• Разработать программную модель информационной системы образовательного процесса;
• Произвести анализ работы программной модели.
На защиту выносятся:
• Программная имитационная модель, позволяющая проводить эксперименты с различными входными параметрами;
• Алгоритм работы программной имитационной модели информационной системы образовательного процесса.
Научная новизна работы заключается в разработке алгоритма работы программной имитационной модели и применении методики к сфере образования.
Практическая значимость:
• Программное обеспечение позволит оценить эффективность образовательных процессов в высшем учебном заведении.
• Текущий программный продукт имеет адаптивную систему, позволяющую любому python разработчику создать дополнительные модули и интегрировать их в техногенную образовательную среду.
• На основании программной модели возможно дальнейшее проведение исследований образовательных процессов с целью повышения их эффективности.
Структура и объем работы: Диссертационная работа состоит из введения, двух глав, заключения, списка литературы, включающего 20 наименований. Работа изложена на 65 страницах, содержит 37 рисунков.
МЕТОДОЛОГИЧЕСКИЕ ОСНОВЫИМИТАЦИОННОГО МОДЕЛИРОВАНИЯ
Методы моделирования систем массового обслуживания
Система массового обслуживания (СМО) – это система, занимающаяся обслуживанием заявок (требований). Чаще всего системы массового обслуживания можно встретить в производстве, бизнесе, сфере услуг. Примерами систем массового обслуживания могут служить билетные кассы, магазины, парикмахерские, кафе.
Как правило, входящий поток в теории массового обслуживания считают простейшим (Пуассоновским) потоком.
Для такого потока частота поступления заявок в систему подчиняется закону распределения Пуассона. Вероятность поступления k заявок за время t вычисляется по формуле 1.1
(1.1)
Важной характеристикой любой системы является время обслуживания заявок в системе. Время обслуживания одной заявки - случайная величина, она может быть описана законом распределения. Чаще всего время обслуживания заявок считают распределенным по экспоненциальному закону, функция распределения которого имеет вид(1.2):
(1.2)
СМО с ожиданием делятся на замкнутые и незамкнутые. К замкнутым относятся системы, в которых поток заявок возникает в самой системе, в незамкнутых системах поток заявок приходит из вне.
В качестве основных показателей эффективности работы СМО выступают вероятность того, что все каналы свободны или заняты, средняя длина очереди, коэффициенты занятости и простоя каналов обслуживания.
Рассмотрим параметр α = l/m. Если α/n < 1, то очередь не может расти безгранично.
Важнейшие характеристики работы СМО(1.3-1.12):
1.
(1.3)
2. Вероятность того, что занято ровно k обслуживающих каналов при условии, что общее число требований, находящихся на обслуживании, не превосходит числа обслуживающих аппаратов:
,при 1≤ k ≤ n (1.4)
3. Вероятность того, что в системе находится /е требований в случае, когда их число больше числа обслуживающих каналов:
при k ≥ n (1.5)
4. Вероятность того, что все обслуживающие каналы заняты:
(1.6)
5. Среднее время ожидания требованием начала обслуживания в
системе:
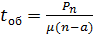(1.7)
6. Средняя длина очереди:
(1.8)
7. Среднее число свободных от обслуживания каналов:
(1.9)
8. Коэффициент простоя каналов:
(1.10)
9. Среднее число занятых обслуживанием каналов:
(1.11)
10. Коэффициент загрузки каналов:
(1.12)
Ниже приводится последовательность расчетов основных
характеристик замкнутых СМО(1.13-1.22).
1. α = l/m - показатель загрузки системы, т.е. математическое
ожидание числа требований, поступающих в систему за время, равное
средней длительности обслуживания:
. (1.13)
2. Вероятность того, что занято k обслуживающих каналов при
условии, что число заявок, находящихся в системе, не превосходит числа
обслуживающих каналов системы:
(1.14)
3. Вероятность того, что в системе находится k заявок для случая, когда
их число больше числа обслуживающих каналов:
(1.15)
4. Вероятность того, что все обслуживающие каналы свободны
откуда 
(1.16)
Величину 
можно получить также путем подстановки в равенство
значений Р1, Р2,..., 
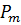, в которые входит сомножителем.
Подставляя их, получаем следующее уравнение для определения 0:
(1.17)
5.Среднее число требований, ожидающих начала обслуживания
(средняя длина очереди):
(1.18)
6. Коэффициент простоя обслуживаемого требования (объекта):
(1.19)
7. Среднее число требований, находящихся в обслуживающей системе, обслуживаемых и ожидающих обслуживания:
(1.20)
8. Среднее число свободных обслуживающих каналов:
= 
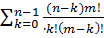(1.21)
9. Коэффициент простоя обслуживающего канала:
(1.22)