Объединенное уравнение для I и II законов термодинамики.

Правило Гесса.

Протекание химических реакций сопровождается перераспределением электронов в молекулах (атомах, ионах и т. д.), что вызывает изменение внутренней энергии и энтальпии системы. Изменение энергии может сопровождаться поглощением или выделением теплоты, а также совершением работы.

Тепловой эффект реакции отождествляется с изменением внутренней энергии для систем c V = const: Qv = ΔU и с изменением энтальпии для систем с р = const: Qp = ΔH.

Правило Гесса устанавливает, что тепловой эффект химической реакции, протекающей при постоянном объеме или постоянном давлении, не зависит от промежуточных реакций, а определяется лишь начальным и конечным состоянием реагирующих веществ.

Во всех остальных случаях правило Гесса недействительно.

Уравнение Кирхгофа.

Зависимость теплового эффекта от температуры определяется по уравнению Кирхгофа.

Изменение энтальпии реакции (или произвольного процесса) при постоянном давлении и повышении температуры на один градус равно сумме теплоемкостей продуктов реакции (процесса), умноженных на стехиометрические коэффициенты, за вычетом теплоемкостей исходных веществ, также умноженных на стехиометрические коэффициенты.

, после интегрирования: ΔH_Т = ΔH_О + (4)

Где a, b, c, d – стехиометрические коэффициенты реакции

aA + bB = cC + dD

Пример. В качестве противопригарной добавки в формовочную смесь вводится марганцевая руда. Для определения количества руды в смеси необходимо знать изменение энтальпии в результате взаимодействия закиси марганца с кварцевым песком при заливке формы металлом при 1500° К:

Решение:

Теплоемкость компонентов реакции находим из справочника

Изменение энтальпии реакции определим по формулам (2) и (4). При расчете сделаем допущение, что каждый из компонентов реакции не испытывает превращений в твердой фазе до температуры 15006 К (на самом деле.кремнезем и закись марганца испытывают ряд фазовых превращений до этих температур, но теплоты этих превращений малы и в первом приближении их можно не учитывать). В этом случае

 

После подстановки числовых значений теплоемкости и стандартных энтальпий получаем

ΔН^о_т= 1240,3—37,143 = 1203,157 кдж/моль.

 

ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ

Этот закон устанавливает определенные закономерностей превращения теплоты в работу и обратно. Являясь двумя формами передачи энергии, теплота и работа не являются равноценными: если работа может непосредственно пойти на увеличение любого вида энергии, то теплота непосредственно, без превращения ее в работу, приводит лишь к увеличению внутренней энергии системы.

Второй закон позволяет разделить все процессы на два вида:
обратимые и необратимые. Мерой необратимости процесса является энтропия – S – параметр состояния тела, полный дифференциал которой меньше, либо равен отношению бесконечно малого приращения затраченной теплоты к температуре процесса: dS =

где — приращение энтропии; — минимальная теплота, подведенная к системе; T — абсолютная температура процесса;

Для обратимого кругового процесса изменение энтропии = нулю (те. сама энтропия является постоянной величиной)

Для необратимого кругового процесса изменение этропии всегда положительно

Соответственно, dS ≥ 0 – II закон термодинамики.

При стремлении системы к равновесию

Lim S → max.

Энтропия является аддитивной величиной — энтропия сложной системы
равна сумме энтропии ее отдельных частей.

Энтропия отдельных частей системы в произвольном процессе
может как возрастать, так и уменьшаться (при возрастании энтропии системы в целом). При любом процессе, ускоряющем движение частиц, энтропия возрастает (плавление, испарение, диффузия и т. д.).

Изменение энтропии при произвольном превращении равно
разности энтропии конечного и начального состояний, т. е.

Объединенное уравнение для I и II законов термодинамики.

Решение системы уравнений (1 з-н) и (2. з-на) позволяет написать объединенное уравнение для первого и второго законов термодинамики для любого компонента системы:

dU = TdS — pdV.

Из последнего уравнения следует, что внутренняя энергия является функцией двух независимых переменных — энтропии и объема, т. е.

U = f(S, V).

Таким образом, U – внутренняя энергия – является характеристической функцией, так как с помощью ее производных можно выразить в явной форме термодинамические параметры системы. Например,

P =- ()_S и T = ()_V;

Таким образом, давление в системе можно выразить как взятую с обратным знаком скорость изменения внутренней энергии по объему при постоянной энтропии системы. Температура в системе равна скорости изменения внутренней энергии по энтропии при постоянном объеме.

Обладая запасом энергии U, система не может эту энергию полностью перевести в полезную работу.

Внутреннюю энергию системы можно представить в виде суммы:

U = F + TS,

где F – cвободная энергия, которая может быть использована для производства работы (ее также называют - св. энергия Гельмгольца, свободная энергия при постоянном объеме, изохорно-изотермический потенциал.);

TS – связанная энергия, которая безвозмездно теряется в процессе.

F – свободная энергия, тоже характеристическая функция, так как с ее помощью можно определить в явной форме ряд термодинамических параметров системы.:

dF = - SdT — pdV..

Таким образом, свободная энергия является функцией двух независимых переменных Т и V. Полный дифференциал функции F можно выразить следующим образом:

И отсюда:

Эти соотношения позволяют, например, рассчитать давление в системе, если известна величина свободной энергии и ее зависимость от объема.

Условием равновесия для изохорно-изотермического процесса является условие минимума функции F при равновесии

dF≤0

Работа при изохорно-изотермическом процессе равна разности свободных энергий:

А_V,T = F₁ – F₂, т.е.

ΔF позволяет судить о направлении процессов в незамкнутых системах, т.к. характеризует максимальную полезную работу.

Для изобарно-изотермического процесса введена функция – свободная энтальпия или термодинамический потенциал Гиббса (св. энергия Гиббса):

G = U + pV — TS = Н — TS.

Полное значение энтальпии можно представить в виде суммы
двух частей:

Н = G + TS = (Н — TS) + TS.

Первая часть характеризует ту энергию, которая может быть использована в процессе (свободная энтальпия), а вторая — энергию, которую невозможно использовать в изобарно-изотермическом процессе (связанная энтальпия).

Так же как и свободная энергия, свободная энтальпия является термодинамическим потенциалом. В дифференциальной форме уравнение свободной энтальпии имеет вид:

dG = - S dT + V dp

Таким образом, свободная энтальпия является функцией двух независимых переменных — температуры и давления.

При постоянной температуре и давлении изменение свободной энтальпии равно нулю, т.е. Т=const, P=const ΔG=0

Полный дифференциал свободной энтальпии можно представить в виде:

dG= , имея в виду предыдущее выражение, можно записать:

V=

S=

Используя эти выражения, зная экспериментальную зависимость свободной энтальпии G от температуры, можно найти значение эН для системы и ΔН для процесса:

Н=G – T

ΔН=ΔG – Эти два выражения называются уравнениями Гиббса.

При самопроизвольном течении изобарно-изотермического процесса свободная энтальпия системы снижается. Для неравновесного процесса dG ≤0 — условие минимума функции G.

Для равновесного процесса dG = 0.

Следовательно, при стремлении процесса к равновесию свободная энтальпия стремится к G_min, и при равновесии она достигает минимального значения.

Для изобарно-изотермического процесса свободная энтальпия связана с работой:

А_р,Т = А_V,Т – pΔV≤G₁ – G₂
Это означает, что термодинамическая функция G может служить критерием направленности протекания изобарно-изотермических процессов.

 

Химический потенциал

Большинство реальных процессов протекает между различными частями системы с переменным числом частиц. Изменение числа частиц в частях системы может быть вызвано различными причинами: механическими, химическими, электромагнитными и т. д.
Общее число частиц в системе при этом может изменяться (большинство химических реакций) или оставаться неизменным (плавление, испарение).

Перемещающиеся частицы несут определенную энергию, которую необходимо учитывать при расчете равновесного состояния системы.

Рассмотрим произвольную систему с переменным числом частиц, но при условии, что ∑n_i= 1 молю. В этом случае вместо числа молей n_i нужно писать мольную долю N_i. Для каждой частицы справедливы законы термодинамики. Поэтому в термодинамические уравнения необходимо ввести член, учитывающий перемещения частиц вещества:

δQ=dU+δA+∑μ_idN_i (адиабатный)

dU=TdS – pdV+∑μ_idN_i (изохорный)

dH=TdS + Vdp+∑μ_idN_i (изобарный)

dF= – SdT – pdV+∑μ_idN_i (изохорно-изотермический)

dG= – SdT + Vdp+∑μ_idN_i (изобарно-изотермический)

где μ_i – коэффициент пропорциональности:

Коэффициент μ_i называется химическим потенциалом компонента и является мерой изменения характеристических функций при перемещении частиц из одной части системы в другую. Наибольшее распространение получило выражение химического потенциала через свободную энтальпию, так как все характеристические функции, кроме AG, зависят от числа частиц в системе.

Для одной 'частицы

G = f₄ (p, Т).
Выражение химического потенциала через ΔG:

Численно μ_i равно изменению свободной энтальпии на одну частицу или на моль вещества.

В дифференциальной форме уравнение для химического потенциала имеет вид:

dμ = — s dT + v dp,

где s —энтропия одной частицы (моля);
v — парциальный объем компонента.

 

Химический потенциал позволяет определить влияние внешних факторов на процессы, протекающие в системе. Все самопроизвольные процессы идут в направлении уменьшения химического потенциала. При этом должно выполняться соотношение:

 

т. е.

∑μ_idN_i = 0,

∑N_idμ_i = 0.

Последнее выражение называется уравнением Гиббса — Дюгема. Оно особенно удобно для исследования фазовых превращений.

Химический потенциал компонента вещества в системе можно
вычислить следующим образом:

где μ_i° (N, Т) — химический потенциал чистого вещества при данной температуре, давлении и агрегатном состоянии в системе.
Или,

где μ_i ° (Т, р_о) — химический потенциал i-ro компонента в фазе при постоянной температуре и давлении р₀ = 1;

μ_i ° (Т, с₀) — химический потенциал i-ro компонента в фазе при постоянной температуре и концентрации с₀=1.

Эти уравнения химического потенциала справедливы лишь для идеальных смесей (твердых, жидких или газообразных). В идеальных растворах (и совершенных – концентрированных и разбавленных) частицы растворенного вещества и растворителя не взаимодействуют друг с другом.

ТЕПЛОВАЯ ТЕОРЕМА НЕРНСТА

Второй закон термодинамики позволяет определить вероятность произвольного процесса, проходящего в исследуемой системе.

Однако для вычисления полноты этого процесса необходимо знать абсолютные значения термодинамических величин, рассчитать которые на основании второго закона термодинамики невозможно.

Числовые значения энтропии, энтальпий, свободных энергий и констант равновесия рассчитывают с точностью до постоянной интегрирования. При этом необходимо, кроме температурных зависимостей термодинамических функций, знать их числовые значения при строго определенных условиях.

Исследования, проведенные В. Нернстом, позволили определить постоянную интегрирования. Опираясь на богатый экспериментальный материал, накопленный при изучении поведения веществ при низких температурах, В. Нернст установил, что разность свободной и внутренней энергии при понижении температуры стремится к нулю быстрее, чем по линейному закону, т. е. в уравнении ΔU — ΔF = TΔS при Т — 0 член ΔS также стремится к нулю. Это значит, что lim ΔS = 0.

Таким образом, при всех изменениях, происходящих в чистых конденсированных веществах при абсолютном нуле, изменение энтропии равно нулю. Последнее утверждение является тепловой теоремой Нернста.

М. Планк предположил, что при абсолютном нуле не только изменение энтропии равно нулю, но и сама энтропия равна нулю (постулат Планка), т. е. ΔS = 0 при Т → 0 и S = 0 при Т — 0.

Равенство энтропии нулю при Т → 0 связано с квантовой природой реальных систем. При абсолютном нуле система должна находиться в единственно возможном состоянии с минимальной энергией. Для ряда веществ (сплавы, аморфные тела, химические соединения), как показывают измерения, энтропия стремится не к нулю, а к некоторой положительной величине. Однако это указывает не на ограниченность постулата Планка, а на то, что указанные вещества не находятся в равновесных состояниях. Cсправедливость теоремы Нернста и постулата Планка принимается для всех систем.

Теорема Нернста и постулат Планка позволяют определять абсолютные значения термодинамических величин при произвольных температурах:

и т. д.

УСЛОВИЯ РАВНОВЕСИЯ ТЕРМОДИНАМИЧЕСКОЙ СИСТЕМЫ

Общие условия равновесия произвольных систем в следующих процессах:

изохорно-изоэнтропийном

изобарно-изоэнтропийном

изохорно-изотермическом

изобарно-изотермическом

При расчете равновесий чаще всего выбирают изохорно-изотермические или изобарно-изотермические процессы.

Равновесие в однородной среде.

Условия равновесия в однородной среде (которая по определению не имеет поверхности раздела) следуют из уравнений. Это равенство температур, давлений, концентраций, химических потенциалов, всех видов энергий во всех точках системы (при отсутствии внешнего поля).

Равновесие в гетерогенной системе.

Химический потенциал произвольного компонента в системе при равновесии должен быть одинаков во всех фазах независимо от числа фаз и компонентов системы. Химический потенциал какого-либо вещества в различных агрегатных состояниях также должен быть одинаков во всех фазах:

μ_i^I = μ_i^II = …= μ_i^K

Это позволяет определить химический потенциал произвольного вещества по парциальному давлению его паров:

μ_i = μ_iº(p, T) + RTlnp_i

 

Уравнение Клаузиуса — Клапейрона.

Процессы изменений фазового состояния вещества, протекающие без химического взаимодействия, называются фазовыми превращениями. Основными характеристиками фазовых превращений являются температура и давление, взаимосвязанные между собой.

Зависимость температуры превращения от давления можно определить из условия равновесия химических потенциалов при равновесии двух фаз:

μ^I(p, T) = μ^II(p, T)

Дифференцируя это уравнение, получим

dμ^I(p, T) = dμ^II(p, T)

или, учитывая, что dμ является полным дифференциалом:

Или:

это выражение называется уравнением Клаузиуса—Клапейрона. Его можно записывают через теплоту фазового превращения:

где Q_np = Т (s" — s') = TΔS — теплота фазового превращения;

v" — v' — изменение объема при фазовом превращении.

Для плавления Q = λ_пл, λ_пл = Т_пл

Для испарения Q = р_ис, p_исп = Т_исп

Из уравнения Клаузиса—Клапейрона следует, что любое превращение в системе, связанное с изменением объема или плотности, имеет температуру превращения, зависящую от давления.
При плавлении металлов и сплавов Т_пл зависит от давления в незначительной степени. Ниже показана зависимость температуры плавления свинца от внешнего давления:

Р, Мн/м2	0,1	25,0	50,0	100,0	200,0
Тпл, °К	623,51	625,62	627,36	631,44	639,54

 

В общем виде уравнение Клаузиуса—Клапейрона не решается, из-за сложной зависимости от температуры.

Однако его можно решить, сделав ряд допущений.

Рассмотрим процесс испарения или разложения конденсированного вещества (твердого или жидкого) с выделением из него газов.

Допустим: 1) объемом конденсированной фазы по сравнению
с газообразной можно пренебречь, т.е. ΔV = V_газ—V_конд = V_газ

2) газ подчиняется уравнению состояния идеальных газов, т. е. для 1 моля

V =

Учитывая допущения, общее решение уравнения Клаузиуса — Клапейрона:

ln

Рассмотрим 3 случая:

1. Энтальпия превращения не зависит от температуры. В этом случае

Или, учитывая значения R=8,314 и модуль перехода ln→lg=2,303

2. Энтальпия превращения не зависит от температуры в интервале температур T₁ — T₂.

В этом случае исследуемый участок температур разбивают на ряд интервалов с ΔH_i = const и общее уравнение интегрируют по частям. В результате получают:

lg

3. Зависимость энтальпии превращения от температуры в общем случае выражается уравнением:

ΔH = ΔH^o + αT + βT²+…

В этом случае решение следующее:

lgp =

Пример:

Плавка чистого магния сопровождается обильным паровыделением легко воспламеняющегося магния (горит в присутствии кислорода воздуха) Чтобы уменьшить испарение магния, его поверхность покрывают слоем шлака. Эффективность такой защиты сохраняется только до температуры кипения магния. Экспериментально установлена зависимость давления паров магния от температуры:

ln p_Mg =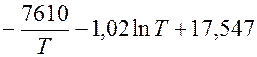

Определить температуру кипения Mg при р = 100 кн/м² (760мм рт.ст.)

Решение.

Температуру кипения Mg при р=100 кн/м² определим по экспериментальной зависимости:

ln 100 =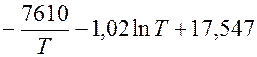

Преобразуем:

1,02 Т lnТ – 12,941Т + 7610 = 0

Т_кип = 1376ºК (1103ºС)

 

 

Правило фаз.

Рассмотрим систему из K независимых компонентов, размещенных в Ф фазах. Химический потенциал каждого компонента μ_к^ф, где нижний индекс обозначает компонент, верхний ‒ фазу.

Состояние гетерогенной системы определяется температурой, давлением и концентрацией.

Для определения концентрации каждого К-го компонента в какой-либо фазе, необходимо знать содержание (К -1) компонентов в той же фазе. Таким образом, для описания состояния системы необходимо решить Ф×(К-1) уравнений.

Однако общее число уравнений может быть сокращено, если учесть, что химический потенциал i-го компонента во всех фазах при равновесии должен быть одинаков:

Таким образом, число независимых уравнений Ф×(К-1) может быть сокращено на К×(Ф-1) уравнений.

Т.О. Число независимых уравнений для определения концентрации каждого компонента равно:

Ф(К-1) – К(Ф-1)=К-Ф.

Число независимых уравнений состояния термодинамической системы равно числу термодинамических степеней свободы с и указывает число независимых параметров, изменение которых (в определенных пределах) не изменяет числа фаз и компонентов системы.

Найденное нами число степеней свободы не учитывает влияние внешних параметров, включая р и Т. По второму постулату термодинамики внутренние параметры системы являются функцией внешних параметров и температуры. Следовательно, к числу степеней свободы необходимо добавить число неучтенных внешних параметров:

с = К - Ф + f.

Это выражение называется уравнением Гиббса—Коновалова.
В металлургии, литейном производстве, материаловедении обычно учитывают р и Т или только Т.

с = K ‒ Ф + 2,

или с = К ‒ Ф+ 1.

 

РАВНОВЕСИЕ ХИМИЧЕСКИХ РЕАКЦИЙ

Рассмотрим равновесие химической реакции догорания окиси углерода:

2СО + О₂ ↔2СО₂; ΔН° = —566 200 дж/моль.

Равновесие всей системы при Т = const, p — const определяется из условия минимума свободной энтальпии, G→min:

ΔG = ∑ΔHº – Т∑ΔS = [2Hº_CO2 – (2Hº_CO + Hº_O2)] – T[2S_CO2 – (2S_CO + S_O2)] = 0

В данной системе все вещества взаимно растворены, поэтому при расчетах необходимо учитывать энтропию смешения:

ΔSсм = –R[2 ln N_CO2 – (2 ln N_CO+ ln N₀₂)]

Ni — мольные доли компонентов в системе.
При постоянной температуре ΔH° и ΔS^o — величины постоянные. Следовательно, и сумма энтропии смешений при постоянной температуре должна быть величиной постоянной, т. е.

2 ln N_CO2 – (2 ln N_CO+ ln N₀₂)= const,

Ln = const,

=K_N = const.

Величина K_N называется константой равновесия, выраженной через мольные доли компонентов реакции. При постоянных температуре и давлении константа равновесия не зависит от количественного соотношения участвующих в реакции веществ. Если изменить концентрацию одного из компонентов реакции, то изменятся концентрации всех других веществ, но таким образом, что константа равновесия останется без изменения.

Для произвольной реакции

аА + bВ +---- ↔ сС + dD + ----

константа равновесия равна

K_N =

где v_i; — стехиометрические коэффициенты реакции;

П — знак произведения.

Знание величины константы равновесия позволяет определить
полноту протекания химических реакций.

При К > 1 — реакция смещается вправо;

K< 1 — реакция смещается влево;

К >> 1 — система состоит в основном из продуктов реакции;

К << 1 — исходная смесь практически не реагирует.

В литейных и металлургических производствах многие процессы протекают в газовой среде, где концентрацию веществ удобнее выражать через парциальные давления.

В этом случае, константу равновесия можно записать через парциальные давления при р₀ = const.:

K_p = = const

Если реакция протекает без изменения числа молей, то

∑v_iкон – ∑v_iнач = 0 и K_p = K_N.

Если концентрация выражается в объемных долях с= или в %,

при Т = const, константа равновесия, выраженная через объемную концентрацию:

K_С = = const

Для реакций, протекающих без изменения числа молей,

K_p = K_N = K_C

Пример. При изготовлении отливок методом литья по выжигаемым моделям возможна реакция

СН₄ + H₂O = 3H₂ + СО.

Определить состав газовой смеси после заливки металла в форму, если исходная смесь состояла из 1 моля метана и 0,1 моля паров воды, а Кр= 1. Считать, что других газов в форме нет.

Решение. Составим материальный баланс реакции:

Компоненты	Н2О	СН4	СО	Н2
Было до реакции Ушло в реакцию В равновесии	0,1 х 0,1 – х	1,0 х 1 – х	- - х	- - 3х
Общее число молей в реакции	1,1 – 2х

 

Следовательно, уравнение константы равновесия реакции запишется в виде:

К_р =

 

Решением этого уравнения является х = 0,0298. Таким образом, в равновесной системе будет находиться

СН₄=0,9702моля; СО=0,0298моля; Н₂О=0,0702 моля; Н₂=0,0894 моля.

 

Чтобы определить направление и полноту протекания химической реакции необходимо знать численное значение константы равновесия.

Для расчета используют уравнение изотермы химической реакции,

условно считая концентрации всех компонентов в исходном состоянии равными 1, свободная энтальпия:

ΔG_пр = – RT ln K_N.

Для систем с постоянным давлением или объемом

ΔG_пр = –RT ln К_р, ΔF_np = –RT ln K_c.

Учитывая, что ΔQ_пр = ΔH_пр – T ΔS_пр, получаем

lnK_N =

При грубых расчетах равновесия процессов в литейном производстве, металлургии и материаловедении энтальпию ΔH и энтропию ΔS обычно определяют по справочнику для стандартных условий, Т = 298,2ºК и р = const =1атм,

lgK_p =

 

По константе равновесия K_N исследуемой реакции можно определить направление процесса при любых исходных и конечных концентрациях веществ, рассчитав ΔG.

Если ΔG > 0, то это значит, что реакция идет в обратном направлении, (справа налево), т.е.в сторону образования исходных веществ.

При ΔG < 0 реакция идет в прямом направлении с образованием продуктов реакции.

 

 

Зависимость константы равновесия от температуры отражают уравнения Вант-Гоффа для изобарно-изотермического процесса:

изобара химической реакции:

Изохорма химической реакции:

Эти уравнения указывают на линейную зависимость ln константы равновесия (при ΔH = const) от 1/T, т.е. угол наклона этой прямой пропорционален тепловому эффекту реакции.

		1/T

 

 

РАСЧЕТ РАВНОВЕСИЯ С ПОМОЩЬЮ АБСОЛЮТНЫХ ЗНАЧЕНИЙ ЭНЕРГИЙ

Порядок расчета следующий:

1) по справочнику определяются теплоемкости, энергии и энтропии компонентов реакции при стандартных условиях (С^ор_298,2, ΔН^о_298,2 ΔS^o_298,2);

2) рассчитываются энергии и энтропии взаимодействия для заданных условий;

3) рассчитываются константы равновесия К_р.

Сначала проводят предварительный расчет, определяя ΔG^o_T(ΔF^o_T) или пренебрегая изменением теплоемкости во время реакции (ΔС_р = 0), или считают это изменение постоянным, не зависящим от температуры, ΔС_р =const.

Если получают ΔG^o_T(ΔF^o_T)<<0, то это означает, что реакция в данных условиях протекает практически полностью.

Если ΔG^o_T(ΔF^o_T)>>0, то реакция практически не идет.

В этих случаях надобность в точном расчете отпадает.

Расчет проводят при отсутствии фазовых превращений в изохорно-изотермической системе по выражению:

(1)

При ΔC_p = О

Если ΔC_p = const, то

Итак, приблизительный расчет выполнили, решили, что точный расчет необходим. Проводим его по уравнению (1), преобразовав в более удобную форму:

Значения двойных интегралов находят в справочниках для различных значений температур.

В справочниках приведены значения коэффициентов разложения этих двойных интегралов в ряд по методу Темкина-Шварцмана:

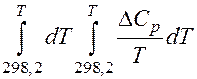= ΔaM_o+ ΔbM₁+ ΔcM₂+ ΔdM₃+ Δc΄M_-2+…

где Δa(Δb, Δc, Δc΄, Δd) =

Vj — коэффициенты уравнений теплоемкости реагирующих веществ;

Значения коэффициентов М₀, M₁, М₂, М₃, М_-2 приведены в справочниках для различных значений температур.

С учетом указанного разложения уравнение для вычисления
свободной энтальпии записывается в виде:

T(ΔaM_o+ ΔbM₁+ ΔcM₂+ ΔdM₃+ Δc΄M_-2)

Далее вычисляют K по уравнению:

lnK = и по ее величине и знаку судят о направлении и полноте реакции.

Следует знать, что связь константы равновесия со свободной энтальпией — одна из наиболее важных зависимостей в термодинамике. Небольшая ошибка в определении ΔG повлечет за собой принципиально неверное значение K.

Наиболее часто встречающееся значение свободной энтальпии равно примерно 200 кдж/моль. Таким образом, ошибка 4% в величине ΔG может привести к ошибке 100% при определении К.

Поэтому ясно, что необходима исключительная точность при вычислении свободной энтальпии, если ее используют для расчетов константы равновесия.