B - Дождь идет тогда и только тогда, когда открыта форточка.
2. ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ И ТАБЛИЦЫИСТИННОСТИ
1) Отрицание (инверсия,, «НЕ», NOT): Если высказывание A истинно, то " не А " ложно, и наоборот.
| A | A |
Таблица истинности
Таблица истинности логического выражения Х – это таблица, где в левой части записываются все возможные комбинации значений исходных данных, а в правой – значение выражения Х для каждой комбинации.
2) Конъюнкция (логическое умножение, Λ, «И», &, AND)
Высказывание " A и B " истинно тогда и только тогда, когда А и B истинны одновременно.
| А | В | А Λ В |
конъюнкция – от лат. conjunctio — соединение.
3) Дизъюнкция (логическое сложение, V, «ИЛИ», OR)
Высказывание " A и B " истинно тогда и только тогда, когда А и B истинны одновременно.
| А | В | АVВ |
дизъюнкция – от лат. disjunctio — разъединение.
4) Импликация (следование, →,«ЕСЛИ..., ТО...»)
Высказывание " A ® B " ложно только если А истинно, а В ложно.
| А | В | А →В |

5) Эквивалентность (~, «)
Высказывание " A «B " истинно тогда и только тогда, когда А и B равны.
| А | В | А «В |
6) Операция "исключающее ИЛИ"
Высказывание "A Å B" истинно тогда, когда истинно А или B, но не оба одновременно.
| А | В | АÅВ |
Логические операции имеют следующий приоритет:
1. Действия в скобках
2. Инверсия
3. Конъюнкция Λ
4. Дизъюнкция V
5. Импликация →
6. Эквивалентность «
3. ЛОГИЧЕСКИЕ ЗАКОНЫИ ПРАВИЛА ПРЕОБРАЗОВАНИЯ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ
1. Закон двойного отрицания:
(А)=А.
2. Переместительный (коммутативный) закон:
А V B = B V A;
A Λ B = B Λ A.
3. Сочетательный (ассоциативный) закон:
(A V B) V C = A V (B V C);
(A Λ B) Λ C = A Λ (B Λ C).
4. Распределительный (дистрибутивный) закон:
(A V B) Λ C = (A Λ C) V (B Λ C);
(A Λ B) V C = (A V C) Λ (B V C).
5. Закон общей инверсии (законы де Моргана):
(АVВ)= А Λ В;
(А Λ В)= А V В.
6. Закон идемпотентности (равносильный):
A V A = A;
A Λ A = A.
7. Законы исключения констант:
A V 1 = 1, A V 0 = A;
A Λ 1 = A, A Λ 0 = 0.
8. Закон противоречия:
A ΛА= 0.
9. Закон исключения третьего:
A V А = 1.
10. Закон поглощения:
A V (A Λ B) = A;
A Λ (A V B) = A.
11. Закон исключения (склеивания):
(A Λ B) V (А Λ B) = B;
(A V B) Λ (А V B) = B.
12. Закон контрапозиции (правило перевертывания):
(A V B) = (B V A).
13. Закон контрапозиции:
А→В=А→В.
14. Правила исключения импликации:
А→В=А V В.
15. Правила исключения эквиваленции:
А « В=(А→В) Λ(В→А).

Упрощение логических выражений
Шаг 1. Заменить операции Å®«на их выражения через И, ИЛИ и НЕ.
Шаг 2. Раскрыть инверсию сложных выражений по формулам де Моргана.
Шаг 3. Используя законы логики, упрощать выражение, стараясь применять закон исключения третьего.
Алгоритм построения таблицы истинности:
- Подсчитать количество переменных n в логическом выражении;
- Определить число строк в таблице, которое равно m = 2n;
- Подсчитать количество операций в логическом выражении и определить количество столбцов в таблице, которое равно количеству переменных плюс количество операций;
- Ввести названия столбцов таблицы в соответствии с последовательностью выполнения логических операций с учетом скобок и приоритетов;
- Заполнить столбцы входных переменных наборами значений;
- Провести заполнение таблицы значениями (0 и 1) истинности по столбцам, выполняя логические операции.
Например: построить таблицу истинности для логического выражения Y=(A→(B→C))~(A Λ B Λ C)
| A | B | C | B→C | A→(B→C) | (A→(B→C)) | C | A Λ B | A Λ B Λ C | Y |
4. ЛОГИЧЕСКИЕ ОСНОВЫКОМПЬЮТЕРА
Всякое устройство ЭВМ, выполняющее некоторое действие над цифровыми сигналами, можно рассматривать как функциональный преобразователь, на входы которого с помощью цифровых сигналов подаются значения аргументов функции (исходные двоичные числа), а на выходах получают значения функций, реализующих указанное действие для этих аргументов (выходные двоичные числа).
Логический элемент компьютера - это часть электронной логической схемы, которая реализует элементарную логическую функцию.
1) Логический элемент «И» (конъюнктор). Выдает на выходе значение логического произведения входных сигналов

Рис. 1
2) Логический элемент «ИЛИ» (дизъюнктор). Выдает на выходе значение логического сложения входных сигналов

Рис.2
3) Логический элемент «НЕ» (инвертор). Выдает на выходе сигнал, противоположный сигналу на входе.

Рис. 3

Пример. Определить структурную формулу по заданной функциональной схеме

Решение:
1. Переменные А и В входят в «коробочку» ИЛИ, полученная формула на выходе – (А Ú В)
2. Пройдя «коробочку» ИЛИ сигнал заходит в «коробочку» НЕ, полученная формула на выходе – не (А Ú В)
3. Переменная В тоже проходит через «коробочку» НЕ, полученная формула на выходе – не В
4. Далее на пути встречается «коробочка» И, пройдя через которую переменные приходят к виду F = не (А Ú В) и (не В)
Запишем соответствующие формулы на схеме:

ПРИМЕРЫТИПОВЫХ РЕШЕНИЙ
Задача №1
Укажите, какое логическое выражение равносильно выражению AÙ(BÚC)
1) A Ú B Ú C
2) A Ú B Ú C
3) A Ù B Ù C
4) A Ù B Ù C
Решение (использование законов де Моргана):
1. Перепишем заданное выражение и ответы в других обозначениях:
заданное выражение 
ответы: 1)  2)
2)  3)
3) 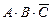 4)
4) 
2. Посмотрев на заданное выражение, видим инверсию (операцию «НЕ») для сложного выражения в скобках, которую раскрываем по формуле де Моргана,

а затем используем закон двойного отрицания по которому  :
:

3. Таким образом, правильный ответ – 3.
Задача №2
Сколько различных решений имеет уравнение
((K\/L) /\ (M\/N)) = 1,
где K, L, M, N – логические переменные?
В ответе не нужно перечислять все различные наборы значений K, L, M и N, при которых выполнено данное равенство. В качестве ответа Вам нужно указать количество таких наборов.
Решение
((K\/L) /\ (M\/N)) = 1
| K | L | M | N | K\/L | M\/N | (K\/L) /\ (M\/N) |
Ответ: 9
Задача №3
Пример 1. Для какого из указанных значений числа X истинно высказывание ((X>2) -> (X>3))
1) 1
2) 2
3) 3
4) 4
Решение.
1) Определим порядок действий: сначала вычисляются результаты отношений в скобках, затем выполняется импликация (поскольку есть «большие» скобки), затем – отрицание (операция «НЕ») для выражения в больших скобках.
2) Выполним операции для всех приведенных возможных ответов (1 обозначает истинное условие, 0 – ложное); сначала определяем результаты сравнения в двух внутренних скобках:
| X | X > 2 | X > 3 | (X > 2)→(X > 3) | ((X > 2)→(X > 3)) |
3) По таблице истинности операции «импликация» находим третий столбец (значение выражения в больших скобках), применив операцию «импликация» к значениям второго и третьего столбцов (в каждой строке):
| X | X > 2 | X > 3 | (X > 2)→(X > 3) | ((X > 2)→(X > 3)) |
4) Значение выражения равно инверсии третьего столбца (меняем 1 на 0 и наоборот):
| X | X > 2 | X > 3 | (X > 2)→(X > 3) | ((X > 2)→(X > 3)) |
5) Таким образом, ответ – 3.
Решение (вариант 2, упрощение выражения):
1) Обозначим простые высказывания буквами:
A = X > 2, B = X > 3.
2) Тогда можно записать все выражение в виде
(A → B) или  .
.
3) Выразим импликацию через «ИЛИ» и «НЕ» (см. выше):
(A → B)= (A Ú B) или  .
.
4) Раскрывая по формуле де Моргана операцию «НЕ» для всего выражения, получаем
(A Ú B)= A Ù B или 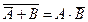 .
.
5) Таким образом, данное выражение истинно только тогда, когда A истинно (X > 2), а B – ложно (X ≤ 3), то есть для всех X, таких что 2 < X ≤ 3.
6) Из приведенных чисел только 3 удовлетворяет этому условию,
7) Таким образом, ответ – 3.
Выводы:
1) В данном случае, наверное, проще первый вариант решения (прямая подстановка всех предложенных ответов)
2) Второй вариант позволяет не только проверить заданные значения, но и получить общее решение – все множество X, для которых выражение истинно; это более красиво для человека, обладающего математическим складом ума.
Задача №4
Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
| X | Y | Z | F |
Какое выражение соответствует F?
1)X \/ Y \/ Z
2) X /\ Y /\ Z
3) X /\ Y /\ Z
4) X \/ Y \/ Z
Решение.
Рассмотрим выражение X \/ Y \/ Z:
1) X=0, Y=0, Z=0, F=0
0 \/ 0 \/0=0;
2) X=1, Y=1, Z=0, F=1
1 \/1 \/0=1;
3) X=1, Y=0, Z=0, F=1
1 \/0 \/0=1.
Ответ: 4
Задача №5
Три школьника, Миша (М), Коля (К) и Сергей (С), остававшиеся в классе на перемене, были вызваны к директору по поводу разбитого в это время окна в кабинете. На вопрос директора о том, кто это сделал, мальчики ответили следующее:
Миша: «Я не бил окно, и Коля тоже…»
Коля: «Миша не разбивал окно, это Сергей разбил футбольным мячом!»
Сергей: «Я не делал этого, стекло разбил Миша».
Стало известно, что один из ребят сказал чистую правду, второй в одной части заявления соврал, а другое его высказывание истинно, а третий оба факта исказил. Зная это, директор смог докопаться до истины.
Кто разбил стекло в классе? В ответе запишите только первую букву имени.
Решение.
| М | К | С | |
| М | |||
| К | |||
| С | |||
| истинно |
Значит, Сергей сказал правду, Коля соврал, Миша в одной части заявления соврал, а другое его высказывание истинно
Сергей: Сергей не бил, Миша бил;
Коля: Миша бил, Сергей не бил;
Миша: Коля не бил, Миша бил.
Ответ: М.
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
Задача №1
Вариант №1
Укажите, какое логическое выражение равносильно выражению (AÚBÚC)?
1) A Ú B Ú C
2) A Ù B Ù C
3) A Ú B Ú C
4) A Ù B Ù C
Вариант №2
Какое логическое выражение равносильно выражению
(A Ù B) Ù C?
1) A Ú B Ú C
2) (A Ú B) Ù C
3) (A Ú B) Ù C
4) A Ù B Ù C
Вариант №3
Укажите, какое логическое выражение равносильно выражению (А Ù B)?
1) A Ú B
2) A Ú B
3) B Ù A
4) A Ù B
Вариант №4
Какое логическое выражение равносильно выражению
(А Ú B)?
1) A Ú B
2) A Ù B
3) A Ú B
4) A Ù B
Вариант №5
Какое логическое выражение эквивалентно выражению
(A Ú B) Ù C?
1) (A Ú B) Ú C
2) A Ù B Ù C
3) (A → B)Ú C
4) (A Ú B)Ú C
Вариант №6
Какое логическое выражение эквивалентно выражению
A Ù (B Ù C)?
1) A Ù B Ù C
2) A Ú B Ú C
3) A Ù (B Ú C)
4) (A Ú B) Ù C
Вариант №7
Какое логическое выражение эквивалентно выражению
(A Ú B) Ù C?
1) (A Ú B) Ù C
2) (A Ù B) Ù C
3) (A Ù B) Ù C
4) (A Ú B) Ù C
Вариант №8
Какое логическое выражение эквивалентно выражению
(A Ú B) Ù C?
1) A Ú B Ù C
2) (A Ù B) Ù C
3) (A Ú C) Ú B
4) (A Ú C) Ù B
Вариант №9
Какое логическое выражение эквивалентно выражению
(A Ù B) Ù C?
1) (A Ù B) Ù C
2) (A Ú B) Ú C
3) (A Ù B) Ú C
4) (A Ú B) Ù C
Вариант №10
Какое логическое выражение эквивалентно выражению
(A Ú B) → C?
1) A Ù B Ù C
2) A Ú B Ú C
3) (A Ú B) Ú C
4) A Ú B Ú C
Вариант №11
Какое логическое выражение эквивалентно выражению
(A Ú B)Ù C?
1) A Ú B Ú C
2) (A Ú B)Ù C
3) (A Ú B)Ù C
4) A Ù B Ù C
Вариант №12
Какое логическое выражение эквивалентно выражению
A Ù (B Ú C)?
1) A Ù B Ù C
2) A Ú B Ú C
3) A Ù B Ù C
4) A Ú B Ú C
Вариант №13
Какое логическое выражение эквивалентно выражению
A Ù (B Ú C)?
1) A Ù B Ù C
2) (A Ù B) Ú C
3) (A Ù B) Ú C
4) A Ù B Ù C
Вариант №14
Какое логическое выражение равносильно выражению
А Ú (BÚ C)?
1) A Ù B Ù C
2) A Ù B Ú C
3) A Ù (B Ù C)
4) A Ú B Ú C
Вариант №15
Укажите, какое логическое выражение равносильно выражению
AÚ(BÙC)?
1) A Ú B Ú C
2) A Ú B Ú C
3) A Ù (B Ù C)
4) A Ú B Ú C
Вариант №16
Укажите, какое логическое выражение равносильно выражению (AÚB)ÚC?
1) (A ÙB) Ú C
2) A Ú B Ú C
3) (A Ù B) Ú C
4) A Ú B Ú C
Вариант №17
Укажите, какое логическое выражение равносильно выражению AÙ(BÚC)?
1) A Ú B Ú C
2) A Ù B Ù C
3) A Ù B Ù C
4) A ÙB Ù C
Вариант №18
Укажите, какое логическое выражение равносильно выражению (AÙBÙC):
1) A Ú B Ù C
2) A Ú B Ú C
3) A Ú B Ú C
4) A Ù B Ù C
Вариант №19
Какое логическое выражение равносильно выражению (AÙB)ÙC)?
1) A ÚB ÚC
2) (A ÚB) Ù C
3) (A Ú B) Ù C
4) A Ù B Ù C
Вариант №20
Укажите, какое логическое выражение равносильно выражению (AÚB)ÙC:
1) A Ú B Ú C
2) A Ù B Ù C
3) (A Ú B)Ù C
4) (A Ù B) Ú C
Задача №2
Вариант №1
Дано логическое выражение (M \/ L) –> (K \/ L \/ N)
Укажите значения переменных K, L, M, N, при которых логическое выражение ложно.
Ответ запишите в виде строки из четырех символов – значений переменных K, L, M и N (в указанном порядке). Так, например, строка 0101 соответствует тому, что K = 0, L = 1, M = 0, N = 1.
Вариант №2
Дано логическое выражение (K –> M) \/ (L/\M /\K)\/N
Укажите значения переменных K, L, M, N, при которых логическое выражение ложно.
Ответ запишите в виде строки из четырех символов – значений переменных K, L, M и N (в указанном порядке). Так, например, строка 0001 соответствует тому, что K = 0, L = 0, M = 0, N = 1.
Вариант №3
Каково наибольшее целое число X, при котором истинно высказывание (X < ·X) → (X < (X-1))
Вариант №4
Сколько различных решений имеет уравнение (KÙLÙM)Ú(LÙ MÙN)= где K, L, M, N – логические переменные? В ответе не нужно перечислять все различные наборы значений K, L, M и N, при которых выполнено данное равенство. В качестве ответа вам нужно указать только количество таких наборов.
Вариант №5
Укажите значения переменных K, L, M, N, при которых логическое выражение (K Ú M) → (L Ú M Ú N) ложно. Ответ запишите в виде строки из четырех символов: значений переменных K, L, M и N (в указанном порядке). Так, например, строка 1101 соответствует тому, что K=1, L=1, M=0, N=1.
Вариант №6
Каково наименьшее целое положительное число X, при котором высказывание: (4 > -(4 + X)·X)) → (30 > X·X) будет ложным.
Вариант №7
Каково наибольшее целое положительное число X, при котором истинно высказывание: ((X - 1) < X) → (40 > X·X)
Вариант №8
Укажите значения переменных K, L, M, N, при которых логическое выражение ((M Ú L) Ù K) → ((K Ù M) Ú N) ложно. Ответ запишите в виде строки из четырех символов: значений переменных K, L, M и N (в указанном порядке). Так, например, строка 1101 соответствует тому, что K=1, L=1, M=0, N=1.
Вариант №9
Каково наименьшее натуральное число X, при котором высказывание
(X·X < 9) → (X >(X + 2)) будет ложным?
Вариант №10
Укажите значения логических переменных Р, Q, S, Т, при которых логическое выражение (Р Ú Q) Ú (Q → (S Ú Т)) ложно. Ответ запишите в виде строки из четырех символов: значений переменных Р, Q, S, T (в указанном порядке).
Вариант №11
Каково наибольшее целое положительное число X, при котором высказывание: ((X + 6)·X + 9 > 0) → (X·X > 20) будет ложным?
Вариант №12
Составьте таблицу истинности для логической функции X=(А → B)Ù(C↔(BÚ A)) в которой столбец значений аргумента А представляет собой двоичную запись числа 226, столбец значений аргумента В – числа 154, столбец значений аргумента С – числа 75. Число в столбце записывается сверху вниз от старшего разряда к младшему. Переведите полученную двоичную запись значений функции X в десятичную систему счисления.
Вариант №13
Составьте таблицу истинности для логической функции X=(А → B)Ù(B↔(C → A)) в которой столбец значений аргумента А представляет собой двоичную запись числа 216, столбец значений аргумента В – числа 30, столбец значений аргумента С – числа 170. Число в столбце записывается сверху вниз от старшего разряда к младшему. Переведите полученную двоичную запись значений функции X в десятичную систему счисления.
Вариант №14
Известно, что для чисел X, Y и Z истинно высказывание (Z<XÚZ<Y)Ù(Z+1<X)Ù(Z+1<Y). Чему равно Z, если X=25 и Y=48?
Вариант №15
Укажите значения переменных K, L, M, N, при которых логическое выражение (K → M) Ù (L Ù K) Ú N ложно. Ответ запишите в виде строки из четырех символов: значений переменных K, L, M и N (в указанном порядке). Так, например, строка 1101 соответствует тому, что K=1, L=1, M=0, N=1.
Вариант №16
Укажите значения переменных K, L, M, N, при которых логическое выражение (K → M) Ù(K → M) Ù (K → (M Ù L Ù N)) истинно. Ответ запишите в виде строки из четырех символов: значений переменных K, L, M и N (в указанном порядке). Так, например, строка 1101 соответствует тому, что K=1, L=1, M=0, N=1.
Вариант №17
Сколько различных решений имеет уравнение JÙ(KÙLÙM)Ù(NÚN)=0 где J K, L, M, N – логические переменные? В ответе не нужно перечислять все различные наборы значений J K, L, M, N, при которых выполнено данное равенство. В качестве ответа вам нужно указать только количество таких наборов.
Вариант №18
Сколько различных решений имеет уравнение (KÙLÙM)Ú(LÙMÙN)=0 где K, L, M, N – логические переменные? В ответе не нужно перечислять все различные наборы значений K, L, M и N, при которых выполнено данное равенство. В качестве ответа вам нужно указать только количество таких наборов.
Вариант №19
Укажите значения переменных K, L, M, N, при которых логическое выражение (KÚM) → (LÚMÚN) ложно. Ответ запишите в виде строки из четырех символов: значений переменных K, L, M и N (в указанном порядке). Так, например, строка 1101 соответствует тому, что K=1, L=1, M=0, N=1.
Вариант №20
Каково наибольшее целое число X, при котором истинно высказывание (50<X·X) → (50>(X+1) (X+1))?
Задача №3
Вариант №1
Для какого числа X истинно высказывание ((X>3) \/(X<3)) –> (X<1)
1) 1
2) 2
3) 3
4) 4
Вариант №2
Для какого числа X истинно высказывание ((X>2) \/(X<2)) -> (X>4)
1)1
2) 2
3) 3
4) 4
Вариант №3
Для какого числа X истинно высказывание ((X>3) -> (X>4))
1)1
2) 2
3) 3
4) 4
Вариант №4
Для какого из указанных значений числа X истинно высказывание ((X < 5)→(X < 3)) Ù ((X < 2)→(X < 1))
1) 1
2) 2
3) 3
4) 4
Вариант №5
Для какого числа X истинно высказывание ((X > 3)Ú(X < 3)) →(X < 1)
1) 1
2) 2
3) 3
4) 4
Вариант №6
Для какого числа X истинно высказывание X > 1 Ù ((X < 5)→(X < 3))
1) 1
2) 2
3) 3
4) 4
Вариант №7
Для какого имени истинно высказывание: (Первая буква имени гласная → Четвертая буква имени согласная)?
1) ЕЛЕНА
2) ВАДИМ
3) АНТОН
4) ФЕДОР
Вариант №8
Для какого символьного выражения неверно высказывание: Первая буква гласная → (Третья буква согласная)?
1)abedc
2)becde
3) babas
4) abcab
Вариант №9
Для какого числа X истинно высказывание (X > 2)Ú(X > 5)→(X < 3)
1) 5
2) 2
3) 3
4) 4
Вариант №10
Для какого из значений числа Z высказывание ((Z > 2)Ú(Z > 4)) →(Z > 3) будет ложным?
1) 1
2) 2
3) 3
4) 4
Вариант №11
Для какого имени истинно высказывание: (Первая буква имени согласная → Третья буква имени гласная)?
1) ЮЛИЯ
2) ПЕТР
3) АЛЕКСЕЙ
4) КСЕНИЯ
Вариант №12
Для какого из значений числа Y высказывание (Y < 5) Ù ((Y > 1) → (Y > 5)) будет истинным?
1) 1
2) 2
3) 3
4) 4
Вариант №13
Для какого символьного выражения верно высказывание: (Первая буква согласная) Ù (Вторая буква гласная)?
1) abcde
2) bcade
3) babas
4) cabab
Вариант №14
Для какого имени истинно высказывание: (Вторая буква гласная → Первая буква гласная) Ù Последняя буква согласная?
1) ИРИНА
2) МАКСИМ
3) МАРИЯ
4) СТЕПАН
Вариант №15
Для какого имени истинно высказывание: (Первая буква согласная → Последняя буква гласная) Ù Вторая буква согласная?
1) ИРИНА
2) СТЕПАН
3) МАРИНА
4) ИВАН
Вариант №16
Для какого имени истинно высказывание: (Первая буква согласная → Вторая буква согласная) Ù Последняя буква гласная?
1) КСЕНИЯ
2) МАКСИМ
3) МАРИЯ
4) СТЕПАН
Вариант №17
Для какого имени истинно высказывание: (Вторая буква гласная → Первая буква гласная) Ù Последняя буква согласная?
1) ИРИНА
2) МАКСИМ
3) МАРИЯ
4) СТЕПАН
Вариант №18
Для какого числа X истинно высказывание ((X>2) → (X>3))?
1) 1
2) 2
3) 3
4) 4
Вариант №19
Для какого символьного выражения верно высказывание: Первая буква слова гласная → Пятая буква согласная → Вторая буква гласная?
1) АРБУЗ
2) ОТВЕТ
3) КРЕСЛО
4) ПРИВЕТ
Вариант №20
Для какого символьного выражения верно высказывание: (Первая буква слова согласная (Вторая буква слова гласная → Последняя буква гласная)
1) ГОРЕ
2) ПРИВЕТ
3) КРЕСЛО
4) ЗАКОН
Задача №4
Вариант №1
Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
| X | Y | Z | F |
Какое выражение соответствует F?
1)X \/ Y \/ Z
2) X /\ Y /\ Z
3) X /\ Y /\ Z
4) X \/ Y \/ Z
Вариант №2
Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
| X | Y | Z | F |
Какое выражение соответствует F?
1)X \/ Y \/ Z
2) X /\ Y /\ Z
3) X /\ Y /\ Z
4) X \/ Y \/ Z
Вариант №3
Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
| X | Y | Z | F |
Какое выражение соответствует F?
1)X \/ Y \/ Z
2) X /\ Y /\ Z
3) X /\ Y /\ Z
4) X \/ Y \/ Z
Вариант №4
Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
| X | Y | Z | F |
Какое выражение соответствует F?
1) X Ù Y Ù Z
2) X Ù Y Ù Z
3) X Ú Y Ú Z
4) X Ú Y Ú Z
Вариант №5
Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
| X | Y | Z | F |
Какое выражение соответствует F?
1) X Ù Y Ù Z
2) X Ù Y Ù Z
3) X Ù Y Ù Z
4) X Ú Y Ú Z
Вариант №6
Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
| X | Y | Z | F |
Какое выражение соответствует F?
1) X Ú Y Ú Z
2) X Ù Y Ù Z
3) X Ù Y Ù Z
4) X Ú Y Ú Z
Вариант №7
Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
| X | Y | Z | F |
Какое выражение соответствует F?
1) X Ú Y Ú Z
2) X Ù Y Ù Z
3) X Ù Y Ù Z
4) X Ú Y Ú Z
Вариант №8
Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
| X | Y | Z | F |
Какое выражение соответствует F?
1) X Ù Y Ù Z
2) X Ù Y Ù Z
3) X Ù Y Ù Z
4) X Ù Y Ù Z
Вариант №9
Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
| X | Y | Z | F |
Какое выражение соответствует F?
1) X Ù Y Ù Z
2) X Ú Y Ú Z
3) X Ú Y Ú Z
4) X Ú Y Ú Z
Вариант №10
Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
| X | Y | Z | F |
Какое выражение соответствует F?
1) X Ù Y Ù Z
2) X Ú Y Ú Z
3) X Ù (Y Ú Z)
4) (X Ú Y) Ù Z
Вариант №11
Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
| X | Y | Z | F |
Какое выражение соответствует F?
1) X Ú Y Ù Z
2) X Ú Y Ú Z
3) X Ù Y Ú Z
4) X Ú Y Ù Z
Вариант №12
Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
| X | Y | Z | F |
Какое выражение соответствует F?
1) (X Ù Y) Ù Z
2) (X Ú