Задания и примеры решения ИДЗ . заочники

3.1. Равновесие тяжелой нити с малой стрелой провисания под дейст­вием вертикальной кусочно-равномерной на­грузки и сосредоточенной силы

 

Нерастяжимая нить длиной L=16,2м с малой стрелой провисания находится в равнове­сии под действием вертикальной кусочно-равномерной распределенной по горизонтальной оси нагрузки и сосредото­ченной силы G=120 Н, прило­женной в точке С нити.

Величина распре­деленной нагрузки, отнесённая к единице длины горизон­тальной оси равна q₁=4 Н/м, q₂=8 Н/м, q₃=12 Н/м. Нить закреплена в опорах А и В, расстояние между которыми по горизонтали равно l= 16 м, по вертикали h =1 м. Абсциссы точек С и Д соответственно равны х₁=6 м, х₂=12 м (рис.15).

Определить уравнения формы кривой равновесия нити и закон изменения натяже­ния вдоль нее. Построить кривую равновесия нити и график изменения натяже­ния в точках нити. Определить реакции в опорах. А и В.

 

Решение.

Для решения задачи применим метод припасовы­вания решений. Разобьем всю длину нити на три участка АС, СД и ДВ, на каждый из которых действует равно­мерно рас­пределенная по горизонтали вертикальная на­грузка. Поэтому каждый уча­сток нити совпа­дает с отрезком соответствующей параболы, уравнения которых запи­шем в форме

 

; (77)

; (78) , (79)

где первое уравнение относится к участку АС, второе – к участку СД, третье уравне­ние – к участку ДВ; считается, что каждому участку соответствует своя горизонталь­ная составляющая Н_k натяжения нити Т.

Уравнения содержат девять неизвестных , , , С₁, С₂, С₃ и Н₁, Н₂,Н₃, для оп­ределения которых нужно составить еще девять уравнений.

Два уравнения получим, используя граничные условия в опорах А и В. В точке А при x=0 y=0. Подставим эти условия в уравнение (77), которому принадлежит точка А и получим: С₁=0. (80)

В точке В при x= l y= h. Эти граничные условия подставим в уравнение (79):

. (81)

Учитывая, что первая и вторая параболы имеют общую точку С, имеем усло­вие: при х=х₁ у_с⁽¹⁾ = у_с⁽²⁾. Подставим х=х₁ в уравнения (77) и (78) и приравняем их.

. (82)

Второй и третий участки имеют общую точку Д. Подставим значение абсциссы х=х₂ в уравнения (78) и (79) и приравняем их:

. (83)

В точке D вторая и третья параболы имеют общую касательную и, следова­тельно, производные, вычисленные в этой точке, т.е. при х=х₂, должны быть равны между собой. Дифференцируем по х уравнения (78) и (79):

; . (84)

Подставляя в уравнение (84) х=х₂ и приравнивая их, получим пятое равенство:

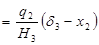. (85)

Еще два равенства получим, состав­ляя условие равновесия точки С нити (рис.16), где приложены три силы: сосредото­ченная сила ; реакция (- ), равная натяже­нию левой части нити (77) и реакция , равная натяжению нити на участке параболы (78).

 

Условие равновесия имеет вид

 

; .

 

 

Спроецируем векторную сумму на оси коорди­нат Ах и Ау:

(86)

(87)

Заметим, что слагаемые в уравнении (86) равны горизонтальным составляю­щим натяжения, т.е.

; , (88)

Поэтому из уравнения (86) получаем

. (89)

 

Из формул (88) выразим натяжения:

; .

Внесем эти значения для Т₁ и Т₂ в уравнение (87):

. (90)

где ; .

Подставим значения 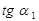и в уравнение (90):

. (91)

Еще одно уравнение получим, рассматривая равновесие точки Д нити (рис.17), где со­гласно условию (85) α₃=α₂=α.

Составляя уравнение равнове­сия сил, прило­женных в точке Д в про­екции на горизонталь­ную ось х, получим:

 

,

где и .

 

Откуда имеем . (92)

 

Решая совместно уравнения (81) - (92), выразим неизвестные параметры че­рез Н.

Умножим уравнение (91) на х₁ и вычтем его из уравнения (82), умноженного на Н, получим

.

Откуда после сложения и приведения подобных выразим

.

Подставим числовые значения

. (93)

Умножим равенство (85) на х₂ и вычтем его из (83), учитывая равенства (90) и (93), .

Выразим отсюда постоянную интегрирования С₃

.

и подставим числовые значения

. (94)

Теперь разрешим уравнение (81) относительно

. (95)

Учитывая выражение (94) для С₃, получим

. (96)

Вычислим значение абсциссы вершины третьей параболы по формуле (95)

. (97)

Абсциссу вершины второй параболы выразим из равенства (85)

, (98)

или, учитывая равенство (97) для :

. (99)

Подставляя в (98) числовые значения, выразим через Н:

. (100)

Из выражения (90) определим

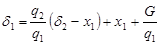. (101)

Подставим выражение (99) для , получим

Вычислим , подставляя числовые значения в выражение (101)

. (102)

Для определения последней неизвестной Н вычислим длину L нити как сумму длин участков парабол: .

Воспользуемся выражением для дифференциала дуги ds нити с малой стрелой про­висания

. (103)

Дифференцируя уравнение (77) по х, находим .

Подставим производную в формулу дифференциала дуги (103)

.

Интегрируя в пределах от 0 до х₁ найдем длину L₁ части параболы, соответствую­щей участку АС нити:

,

. (104)

Внесем значение производной уравнения параболы второго участка из первого ра­венства (84) в выражение дифференциала (103)

и проинтегрируем его в пределах длины второго участка нити от х₁ до х₂

.

Находим длину L₂ ветви второй параболы, соответствующей отрезку нити СД

. (105)

Внесем значение производной из второго равенства (84) в выражение (103) и про­интегрируем его в пределах третьего участка от х₂ до l

.

Находим длину L₃ части третьей параболы, соответствующей участку нити ДВ:

. (106)

Сложим выражения (105) – (107). Получим длину L параболической нити при ма­лой стреле провисания

. (107)

Если подставить в уравнение (107) значения и , выраженные через Н, то оно будет содержать только одну неизвестную величину Н.

Для удобства вычисления преобразуем уравнение (5.32), возводя в куб круглые скобки и группируя слагаемые

.

Подставляя числовые значения и выражения (97), (100) и (102) для , и , окончательно получаем квадратное уравнение относительно Н.

.

Решая квадратное уравнение и взяв перед корнем знак плюс, находим горизон­тальную составляющую натяжения нити

(Н). (108)

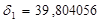По формулам (93), (94), (97), (100), (102) вычислим

м; м;

м; м; м.

Подставляя в уравнения (77), (78), (79) вычисленные значения параметров, соста­вим уравнения, определяющие форму кривой равновесия нити

,

, (109)

.

Для проверки результатов расчета определим ординаты общих точек С и Д сосед­них ветвей парабол.

Подставим значение абсциссы точки С х=х₁ в первые два уравнения (109).

(м),

(м).

Внесем значение абсциссы точки Д х=х₂ во второе и третье уравнения (109):

(м),

(м).

Как видим, значения ординат точек С и Д, вычисленные слева и справа, совпа­дают с точностью до четвертого знака после запятой.

Найдем для каждого участка нити значение параметра а_k

(м),

(м), (110)

(м).

Вычислим теперь стрелки провисания каждой параболы, подставляя в уравне­ния (77), (78) и (79) соответствующие значения координат

(м),

(м), (111)

(м).

Так как каждый участок нити совпадает только с частью параболы, то вычислен­ные значения f_k являются по существу не стрелками нити, а просто значе­ниями соответствующих ординат парабол при .

Натяжение нити на каждом из участков определяем по формуле (43), подстав­ляя значения соответствующих участку параметров

;

; (112)

.

Натяжение нити в точке С приложения сосредоточенной силы, вычис­ленные слева и справа будут различны.

(Н),

(Н)

Для проверки вычислим натяжение нити в точке Д, принадлежащей второй и третьей параболе.

(Н),

(Н).

Как видим, расчеты совпали с точностью до третьего знака после запятой.

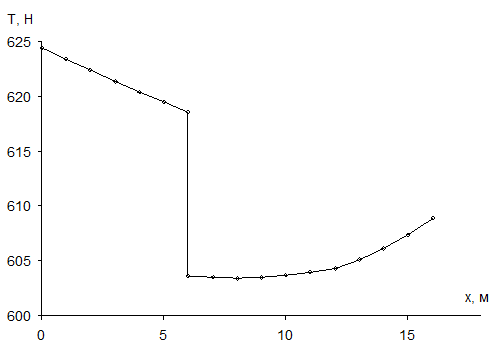
Для построения кривой равновесия нити и графика изменения натяжения вдоль нити за­готовим таблицу 3, используя уравнения (109) и (112).

По точкам строим кривую равновесия нити (рис.18) и график изменения натяже­ния вдоль нити (рис.19).

Реакции в опорах А и В численно равны натяжению нити в этих точках.

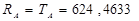Н; Н.

Таблица 3.

№ уч.	х	у	Т	№ уч.	х	у	Т
I участок АС			624,4633			1,4797	603,5235
	0,2605	623,4213		1,4585	603,6930
	0,5144	622,4058		1,4241	603,9685
	0,7616	621,4168		1,3764	604,3501
	1,0023	620,4543	III участок ДВ		1,3763	604,3502
	1,2363	619,5183		1,3121	605,1217
	1,4637	618,6088		1,2279	606,1315
II участок СД		1,4637	603,6514		1,1239	607,3800
	1,4823	603,5027			608,8672
	1,4876	603,4601

 

 

 

Рис.18. Кривая равновесия нити

 

 

4. РАВНОВЕСИЕ НИТИ НА ПОВЕРХНОСТИ

4.1. Равновесие невесомой нити на шероховатой цилиндрической поверхно­сти.

 

Однородная нерастяжимая нить, весом которой можно пренебречь, огибает шерохова­тые поверхности цилиндров 1 и 2. Коэффициент трения нити на поверхности k=0,3.

Рис. 20.

К концу Е нити прикреплен груз 3 ве­сом Р, находящийся на шероховатой плоско­сти, наклоненной под углом α=30◦ к горизонтали. Коэффициент трения груза на плоскости f=0,2. Натяжение конца А нити равно . Определить вес Р груза 3, необходи­мый для равновесия системы. Свободные участки нити считать прямо­линейными.

 

Решение.

Разобьем длину нити на пять участков: участок АВ на шероховатой поверхно­сти цилиндра 1, свободный участок ВС, участок CD шероховатой поверхности цилин­дра 2, свободный участок DE и груз 3.

Примем, что натяжение в точке А нити больше, чем натяжение в точке Е, Т_А>Т_Е.

1. Рассмотрим равновесие нити шероховатой поверхности 1 (рис. 21). Начало от­счета дуговой координаты совместим с точкой А. За положительное направление от­счета дуговой координаты примем направление против хода часовой стрелки.

 

 

Рис. 21.

 

Выберем произвольно точку М и покажем действующие на нить силы, отнесен­ные к единице длины. Касательную ось направим в сторону меньшего натяжения, счи­тая, что натяжение нити в точке В меньше, чем в точке А. Силу трения напра­вим по касательной в сторону уменьшения натяжения, то есть также к точке В. Нормальное давление направим по общей нормали, в противоположную сторону.

Составим дифференциальные уравнения равновесия нити в проекциях на оси есте­ственного трехгранника. Нить расположена по геодезической кривой цилиндра, поэтому угол геодезического отклонения равен нулю, а радиус кривизны нити ра­вен радиусу цилиндра ρ=R.

(113)

Выразим из второго уравнения системы нормальное давление:

и выразив силу трения

подставим ее выражение в первое уравнение системы:

Заменим ds=Rdφ и получим:

Умножая на Rdφ и деля на Т, получим:

.

Проинтегрируем неравенство:

(114)

Для определения постоянной интегрирования С₁, рассмотрим граничные усло­вия в точке А: , . Подставляя граничные условия в неравенство (114) и заме­няя его равенством, получим:

,

то есть

С₁= .

 

Подставляя значение С₁ в неравенство (114), учтя, что разность логарифмов равна ло­гарифму соотношения и потенцируя полученное неравенство, находим натяжение в любой точке нити на участке АВ:

,

,

,

,

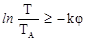(115)

Найдем натяжение в точке В, для которой ,

(116)

Подставив численные значения, получим условие для натяжения в точке В:

Н. (117)

2. Рассмотрим равновесие вертикального участка ВС нити (рис.22).

Примем точку В за начало декартовой системы координат и направим ось Вх вер­тикально вверх.

 

Рис. 22

 

Составим дифференциальное уравнение равновесия нити:

(118)

Так как нить прямолинейна, то есть ds=dx, то дифференциальное уравнение при­нимает вид:

(119)

Для определения постоянной интегрирования С₂ рассмотрим граничные усло­вия в точке В: , . Подставим граничные условия в уравнение (119) и опреде­лим .

Подставляя значение С₂ в равенство (114), получим натяжение в любой точке нити на участке ВС:

(120)

Таким образом, натяжение невесомой прямолинейной нити одинаково в каж­дой точке нити, следовательно . Учитывая условие (117), получим натяжение в точке С нити:

Н. (121)

3. Рассмотрим равновесие нити шероховатой поверхности цилиндра 2 (рис. 23).

Начало отсчета дуговой координаты совместим с точкой С. За положительное на­правление отсчета дуговой координаты примем направление по ходу часовой стрелки.

Выберем произвольно точку М и покажем действующие на нить силы, отнесен­ные к единице длины. Касательную ось направим в сторону меньшего натяже­ния, к точке D, так как приняли, что Т_А>Т_Е. Силу трения направим по каса­тельной в сторону уменьшения натяжения, то есть также к точке D. Нормальное дав­ление направим по общей нормали, в противоположную сторону.

 

 

Составим дифференциальные уравнения равновесия нити в проекциях на оси есте­ственного трехгранника. Нить расположена по геодезической кривой цилиндра, поэтому угол геодезического отклонения равен нулю, а радиус кривизны нити ра­вен радиусу цилиндра ρ=R.

(122)

Выразим из второго уравнения системы нормальное давление:

и выразив силу трения

подставим ее выражение в первое уравнение системы:

Заменим ds=Rdφ и получим:

Умножая на Rdφ и деля на Т, получим:

.

(123)

Для определения постоянной интегрирования С₃, рассмотрим граничные усло­вия в точке С: , . Подставляя граничные условия в неравенство (123) и заме­няя его равенством, получим:

, С₃= .

Подставляя значение С₃ в неравенство (123), находим натяжение в любой точке нити на участке СD:

,

,

,

,

(124)

Получим условие для натяжения в точке D, для которой , :

(125)

Подставив численные значения α=30^◦ и условие для натяжения в точке C (121), най­дем натяжение в точке D:

Н. (126)

 

4. Рассмотрим равновесие отрезка DE нити (рис.24).

Примем точку D за начало декартовой системы координат и направим ось Dх по нити вниз.

 

Составим дифференциальное уравнение равновесия нити:

(127)

Так как нить прямолинейна, то есть ds=dx, то дифференциальное уравнение при­нимает вид:

(128)

Для определения постоянной интегрирования С₄ рассмотрим граничные усло­вия в точке D: , . Подставим граничные условия в уравнение (128) и опреде­лим .

Подставляя значение С₄ в равенство (128), получим натяжение в любой точке нити на участке DE:

(129)

Натяжение невесомой прямолинейной нити одинаково в каждой точке нити, следо­вательно .

Учитывая условие (126), получим натяжение в точке E нити:

Н. (130)

5. Рассмотрим равновесие точки Е нити и груза 3.

Примем точку Е за начало декартовой системы координат и направим ось Ех вниз вдоль плоскости, а Еу – перпендикулярно плоскости, вверх.

 

 

Силу трения направим в сторону, противоположную вероятному движению нити, то есть в сторону уменьшения натяжения. Вес груза - вертикально вниз, натяже­ние точки Е нити – вверх по нити. Реакцию направим перпендикулярно поверхности.

Запишем уравнения равновесия груза в проекциях на оси координат:

, ; (131)

, , (132)

и дополнительное условие равновесия груза

 

Fтр ≤ fN. (133)

Выразим из уравнения (132) нормальное давление плоскости N

и подставим его в неравенство (133):

.

Заменим в уравнении (131) силу трения груза о плоскость полученным неравенст­вом и выразим условие для веса груза:

 

,

,

. (134)

 

Подставив численные значения и условие для натяжения в точке E (130), найдем вес груза 3, необходимый для уравновешивания системы:

 

Н. (135)

Таким образом, натяжение в точке Е меньше, чем натяжение в точке А.

 

4.2. Равновесие тяжелой нити на гладкой цилиндрической поверхности

 

Однородная нерастяжимая нить, весом q=10 Н/м, оги­бает гладкую поверхность цилин­дра 2, перпендику­лярно образующим. Радиус цилиндра равен R=0,5 м. К концу А нити прикреплен груз 1 весом Р=10 Н, находя­щийся на шероховатой, накло­ненной под углом α=30^◦, плоскости. Коэффици­ент трения груза на плоско­сти f=0,23. Длина прямолинейного участка нити АВ =1 м, длина участка СD =0,5 м.

Определить, каким должен быть вес G груза 3, при­крепленного к точке D нити, что бы система находи­лась в равновесии.

 

Решение.

Разобьем длину нити на пять участков: груз 1, свободный участок АВ, участок ВС на гладкой поверхности цилиндра, свободный участок CD и груз 3. Примем, что натяжение в точке D нити больше, чем натяжение в точке А, Т_D>Т_А.

1. Рассмотрим равновесие груза 3. Примем точку D за начало декартовой сис­темы координат и направим ось Dх вер­тикально вверх.

 

Запишем уравнение равновесия груза в проекции на ось Dх:

, ; (136)

Выразим вес G груза: . (137)

2. Рассмотрим равновесие участка CD.

Примем точку D за начало декартовой сис­темы координат и направим ось Dх по нити вверх. Покажем силы, действующие на произвольную точку М.

 

 

 

Составим дифференциальное уравнение равновесия нити:

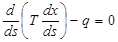(138)

Так как нить прямолинейна, то есть ds=dx, то дифференциальное уравнение при­нимает вид:

(139)

Для определения постоянной интегрирования С₁ рассмотрим граничные усло­вия в точке D: , . Подставим граничные условия в уравнение (139) и опреде­лим .

Подставляя значение С₁ в равенство (139), получим натяжение в любой точке нити на участке СD:

(140)

Определим натяжение точки С нити, в которой , , учитывая усло­вие (2):

,

(141)

3. Рассмотрим равновесие нити гладкой поверхности цилиндра 2 (рис. 29).

Начало отсчета дуговой координаты совместим с точкой С.

Выберем произвольно точку М и покажем действующие на нить силы, отнесен­ные к единице длины. Касательную ось направим в сторону меньшего натяжения, к точке В

 

.

. За положительное направление отсчета дуговой координаты примем направле­ние по ходу часовой стрелки. Нормальное давление направим по общей нормали, в противоположную сторону. Вес единицы длины нити q - вертикально вниз.

Составим дифференциальные уравнения равновесия нити в проекциях на оси есте­ственного трехгранника. Нить расположена по геодезической кривой цилиндра, поэтому угол геодезического отклонения равен нулю, а радиус кривизны нити ра­вен радиусу цилиндра ρ=R.

(142)

Рассмотрим первое уравнение системы, заменив ds=Rdφ:

.

Проинтегрируем равенство

(143)

Для определения постоянной интегрирования С₂, рассмотрим граничные усло­вия в точке С: , . Подставим граничные условия равенство (143):

.

Подставляя значение С₂ в равенство (143), находим натяжение в любой точке нити на участке ВС:

. (144)

Получим условие для натяжения в точке В для которой: , :

. (145)

Подставив условие (141), найдем натяжение в точке В:

. (146)

где β=α.

4. Рассмотрим равновесие отрезка АВ нити (рис.30). Примем точку В за начало де­картовой системы координат и направим ось Вх по нити вниз. Покажем силы, дейст­вующие на произвольную точку М.

 

 

Составим дифференциальное уравнение равновесия нити:

(147)

Так как нить прямолинейна, то есть ds=dx, то дифференциальное уравнение при­нимает вид:

(148)

Для определения постоянной интегрирования С₃ рассмотрим граничные усло­вия в точке В: , . Подставим граничные условия в уравнение (148) и опреде­лим .

Подставляя значение С₁ в равенство (148), получим натяжение в любой точке нити на участке АВ:

(149)

Определим натяжение точки А нити, в которой , .

Учитывая условие (146), получим натяжение в точке A нити:

. (150)

5. Рассмотрим равновесие точки А нити и груза 1. Примем точку А за начало декар­товой системы координат и направим ось Ах вниз вдоль плоскости, а Ау – перпен­дикулярно плоскости, вверх. Силу трения направим в сторону уменьшения на­тяжения. Вес груза - вертикально вниз, натяже­ние точки A нити – вверх по нити. Ре­акцию направим перпендикулярно поверхно­сти.

 

 

Запишем уравнения равновесия груза в проекциях на оси координат:

, ; (151)

, , (152)

и дополнительное условие равновесия груза

Fтр ≤ fN. (153)

Выразим из уравнения (152) нормальное давление плоскости N

и подставим его в неравенство (153):

.

Заменим в уравнении (151) силу трения груза о плоскость полученным неравенст­вом и выразим условие для натяжения нити:

,

. (154)

Найдем натяжение точки А нити, подставив числовые значения:

Н. (155)

Подставим в неравенство значение натяжения Т_А из уравнения (150):

Определим натяжение в точке D:

Н. (156)

 

4.3. Равновесие тяжелой нити на гладкой поверхности цилиндров

 

Рис. 32

Однородная нерастяжимая нить, весом q=10 Н/м, огибает гладкие поверхности цилин­дров 1 и 2, перпендикулярно их обра­зующим. Радиусы цилиндров равны R=0,4м. К концу D нити прикреплен груз 3 ве­сом G=100 Н, находящийся на шероховатой горизонтальной плоскости. Коэффициент трения груза на плоскости f=0,2. Определить, каким должно быть натяже­ние конца А нити, что бы система нахо­дилась в равновесии. Свободный уча­сток нити считать прямолинейным.

 

Решение.

Разобьем длину нити на четыре участка: участок АВ на поверхности цилиндра 1, участок ВС на поверхности цилиндра 2, свободный участок CD, груз 3 на шерохова­той горизонта