числа появления события в независимых испытаниях

Пусть производится n независимых испытаний в каждом из которых вероятность появления события А постоянна и равна p. Чему равно среднее число появлений события А в этих испытаниях?

Теорема

Математическое ожидание М(Х) числа появления события А в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании:

. (2.13)

Пример 4

Вероятность попадания в цель при стрельбе из орудия . Найти математическое ожидание общего числа попаданий, если будет произведено 10 выстрелов.

Попадание при каждом выстреле не зависит от исходов других выстрелов, поэтому рассматриваемые события независимы и, следовательно, искомое математическое ожидание

.

Если - случайная величина, то функция

(2.14)

называется функцией распределения случайной величины . Здесь - - вероятность того, что случайная величина принимает значения, не превосходящие числа .

Функция распределения любой случайной величины обладает следующими свойствами:

· определена на всей числовой прямой R;

· не убывает, т.е. если , то ;

· , , т.е. и

· непрерывна справа, т.е.

Функция распределения содержит всю информация об этой случайной величине и поэтому изучение случайной величины заключается в исследовании ее функции распределения, которую часто называют просто распределением. Так что, когда говорят о нормальном распределении, то подразумевают случайную величину, имеющую нормальную функцию распределения.

У дискретной случайной величины функция распределения ступенчатая.

Пример 5

Случайная величина принимает значение числа очков, выпавшее при однократном бросании кости. Определим ее функцию распределения:

Если - дискретная случайная величина, принимающая значения с вероятностями , то таблица вида

			...		...
			...		...

называется распределением дискретной случайной величины.

Вероятность того, что значение случайной величины попадает в интервал вычисляется для дискретной случайной величины по формуле:

(2.15)

2.3. Биноминальное распределение

Пусть производится n независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Вероятность наступления события во всех испытаниях постоянна и равна p ( следовательно, вероятность непоявления ). Рассмотрим в качестве дискретной случайной величины Х число появлений события А в этих испытаниях.

Поставим перед собой задачу: найти закон распределения величины Х. Для её решения требуется определить возможные значения Х и их вероятности. Очевидно, событие А в n испытаниях либо появится 1 раз, либо 2 раза, …, либо n раз. Таким образом, возможные значения Х таковы: . Остаётся найти вероятности этих возможных значений, для чего достаточно воспользоваться формулой Бернулли:

, (2.16)

где k =0, 1, 2, …, n.

Данная формула и является аналитическим выражением искомого закона распределения.

Распределение, определяемое формулой Бернулли называют биноминальным. Потому что правую часть равенства можно рассматривать как общий член разложения бинома Ньютона.

. (2.17)

Таким образом, первый член разложения определяет вероятность наступления рассматриваемого события n раз в n независимых испытаниях; второй член определяет вероятность наступления события раз; …; последний член определяет вероятность того, что событие не появится ни разу.

Напишем биноминальный закон в виде таблицы:

X n n-1 … k … 0

Р … …

Математическое ожидание для биноминального распределения имеет вид:

, (2.18)

 

Пример 6

Монета брошена 2 раза. Написать в виде таблицы закон распределения случайной величины Х – числа выпадений «герба».

Решение:

Вероятность появления герба в каждом бросании монеты , следовательно вероятность непоявления герба .

При бросании монеты «герб» может появиться либо 2 раза, либо 1 раз, либо совсем не появиться. Таким образом, возможные значения Х таковы: . Найдём вероятности этих возможных значений по формуле Бернулли:

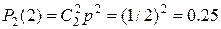
Напишем искомый закон распределения:

Х 2 1 0

Р 0.25 0.5 0.25.

2.4. Распределение Пуассона

Для того чтобы найти вероятность того, что при очень большом числе испытаний, в каждом из которых вероятность события очень мала, событие наступит ровно k раз. При , n – число независимых испытаний, p – вероятность наступления события А. Воспользуемся законом распределения Пуассона вероятностей массовых (n – велико) и редких (p – мало) событий.

(2.19)

Математическое ожидание в этом случае имеет вид:

Пример 1

Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равно 0.0002. Найти вероятность того, что на базу прибудут три негодных изделия.

Решение. По условию, Найдём .

По формуле Пуассона искомая вероятность приближённо равна

2.5. Экспоненциальное распределение

Случайная величина х распределена по экспоненциальному закону, если плотность вероятности имеет вид

, (2.20)

где х – случайная величина, - постоянная.

Если за случайную величину принять время работы до отказа изделия то выражение для плотности вероятности можно переписать в следующем виде:

, (2.21)

где t – время работы до отказа, - интенсивность отказов.

Для характеристик непрерывных распределений используется функция распределения :

. (2.22)

Подставив сюда выражение дл плотности вероятности, получим значение функции распределения для экспоненциального закона:

. (2.23)

Физический смысл функции распределения - это вероятность того, что случайная величина попадает в интервал от 0 до t.

Экспоненциальный закон распределения характеризуется математическим ожиданием (среднее время наработки на отказ)

. (2.24)

Экспоненциальный закон применяется только в тех случаях, когда наблюдается незначительный сбой в работе изделия, а отказы распределены равномерно в равных интервалах времени.

2.6. Простейший поток событий

Потоком событий называют последовательность событий, которые наступают в случайные моменты времени. Примерами потоков событий служат: поступление вызовов на АТС, на пункт неотложной медицинской помощи, прибытие самолётов в аэропорт, клиентов на предприятие бытового обслуживания, последовательность отказов элементов и др.

Формулу Пуассона можно считать математической моделью простейшего потока событий.

, (2.25)

Вероятность появления k событий за промежуток времени, равный t, - интенсивность потока событий.

Пример 2

Среднее число вызовов, поступающих на АТС в одну минуту, равно 2. Найти вероятность того, что за 5 минут поступит а) 2 вызова; б) менее двух вызовов; в) не менее двух вызовов.

Поток вызовов предполагается простейшим.

Решение.

По условию , воспользуемся формулой Пуассона.

а) искомая вероятность того, что за 5 минут поступит 2 вызова

.

Это событие практически невозможно

Б) Событие «не поступило ни одного вызова» и «поступил один вызов» несовместны, поэтому по теореме сложения искомая вероятность того, что за 5 минут поступит менее двух вызовов, равна

Это событие практически невозможно.

В) События «поступило менее двух вызовов» и «поступило не менее двух вызовов» противоположны, поэтому искомая вероятность того, что за 5 минут поступит не менее двух вызовов.

Это событие практически достоверно.

3. КАЧЕСТВО И ЭФФЕКТИВНОСТЬ ИНФОРМАЦИОННЫХ СИСТЕМ

Методы оценки качества

Качество информационной системы – это совокупность свойств системы, обусловливающих возможность её использования для удовлетворения определённых в соответствии с её назначением потребностей.

Обеспечение качества программного обеспечения/ программного изделия (software quality assurance/SQA), являясь одной из составляющей программной инженерии вообще, и технологии программирования в частности, направлено на то, чтобы создать программное обеспечение/изделие (ПО/ПИ), содержащее минимальное количество ошибок (в идеальном варианте вообще без ошибок). Эта проблема включает в себя две, обычно, последовательно решаемые задачи:

1. Упреждение, или предотвращение ошибок (defect prevention oriented SQA) - сделать процесс проектирования ПО/ПИ таким, чтобы минимизировать риск ошибки

2. Удаление ошибок (defect removal oriented SQA) - по возможности, найти и устранить все ошибки, всё - таки “проникшие” в проект.

Задача упреждения решается с использованием:

a) комплекса организационных мер, методик и инструментальных средств, “встроенных” в основную технологию программирования, в используемые в ней языки и трансляторы;

б) методов моделирования – путём создания макетов/прототипов программ и работы с ними;

в) предварительных оценок качества всех промежуточных результатов проектирования и (при необходимости) их корректировкой. Таким образом, оценка качества здесь выступает как один из методов, ориентированных на предотвращение ошибок

В рамках решения второй задачи имеют дело с окончательными/целевыми результатами проектирования, т.е. тем, что так или иначе, раньше или позже поступает к пользователю. При этом исправляемая ошибка должна быть так или иначе обнаружена, для чего необходимо опять - таки оценить качество полученных результатов. Другими словами, оценка качества здесь является одним из методов, ориентированных на удаление ошибок.

Методы оценки качества ПО/ПИ (software evaluation), или просто - оценки, занимают существенное, но далеко не единственное место при решении обеих задач обеспечения качества ПО/ПИ. Соответственно выделяются:
1. Упреждающая оценка, или верификация (software verification), – любая проверка, ориентированная на предотвращение ошибок (оценка в рамках первой задачи

2. Подтверждающая оценка, или технический контроль (software validation), - любая проверка, ориентированная на удаление ошибок, если они будут обнаружены (оценка в рамках второй задачи).
Объектами оценки могут быть компоненты любой природы, входящие в ПО/ПИ, а именно:

1. Программные коды – контроль кодов.

Коды могут быть:

· исходные;

· промежуточные технологические;

· исполняемые;

· интерпретируемые;

· машинные или объектные;

· дистрибутивные – поставляемые;

2. Документы – верификация и контроль документов.

К документам относятся:

· программные документы;

· производственные документы, например, конструкторские документы на материальные составляющие ПИ (носители, упаковка, ярлыки и т.п.);

3. Непосредственно материальные составляющие ПИ – производственный контроль изделия.

Оценка качества может быть:

1. Входной - проверка заимствованных решений (входной контроль/input validation

2. Внутренней или технологической

· проверка промежуточных результатов проектирования;

· рабочая проверка окончательных / целевых результатов проектирования ПО/ПИ (технологический контроль).

3. Выходной – отличается от технологического контроля тем, что производится непосредственно на выходе технологического процесса проектирования / изготовления ПО/ПИ перед передачей его заказчику / пользователю (выходной контроль/ final acceptance validation/end validation/output validation).

К окончательным результатам проектирования/изготовления относятся:

1. Коды программ (обычно имеются ввиду исполняемые коды);

2. Выходные документы – “официальные” редакции программных, конструкторских и других производственных документов, т.е. документы, предназначенные для заказчика и/или входящие в комплект поставки;

3. Материализованные, или производственные результаты, а именно:

· машинные носители с дистрибутивными кодами программ;

· другие материальные составляющие ПИ: упаковка, документы (как объекты изготовления, т.е. книги и машинные носители).

По характеру оценки программ и программных изделий различают:

1. Сатическую(static) оценку - не связанную с прогоном программных кодов. Сюда относится:

· верификация и контроль документов (любых);

· контроль дистрибутивных кодов программ (дистрибутивный контроль);

· статическая верификация программных кодов;

2. Динамическую (dynamic) оценку, или тестирование(testing) – имеющую дело только с программными кодами, которая осуществляется путём их прогона.

3.1. Показатели качества программного изделия

Качество программного изделия сводится к набору значений ряда конкретных характеристик. Их номенклатура зафиксирована в международном стандарте ISO/IES 9126 “Information Technology – Software Product Evaluation – Software Quality Characteristics and Guidelines for their use” (в России он принят под названием ГОСТ ИСО/ИМЭК 9126-93 «Информационная технология. Оценка программной продукции. Характеристики качества и руководство по их применению). В дополнение к нему выпущен стандарт ISO/IES 14598 “Information Technology – Software Product Evaluation”, регламентирующий способы оценки характеристик.

Стандарт ISO/IES 9126 определяет классификационное деление показателей на шесть характеристик.

Функциональные возможности. Функциональные требования традиционно составляют основной предмет определения, моделирования и проверки. Они формулируются в виде утверждений, характеризующих поведение изделия. Для того чтобы устранить отклонения фактического поведения изделия от требуемого, как правило, прежде всего строится формальная модель [10]. И на основании предварительного тестирования обосновывается возможность (или невозможность) удовлетворения функциональных требований.

Надёжность. Надёжность – свойство системы сохранять во времени в установленных пределах значения всех параметров, характеризующих способность выполнять требуемые функции в заданных режимах и условиях применения.

Надёжность информационных систем не самоцель, а средство обеспечения своевременной и достоверной информации на её выходе. Поэтому показатель достоверности функционирования имеет для информационных систем главенствующее значение, тем более, что показатель своевременности информации в общем случае является показателем достоверности.

Практичность. Дать количественную оценку соответствия изделия требованиям удобства практического использования чрезвычайно трудно. Обычно предлагаются методики замеров расхода нормативных единиц труда(нормо-часов), которые пользователи затрачивают как на овладение изделием, так и на прохождение основных вариантов использования. Кроме того используются экспертные балльные оценки, однако при их выполнении следует иметь в виду, что предпочтения пользователей могут существенно расходиться естественным представлением экспертов об удобном интерфейсе.

Эффективность. Эффективность – это свойство системы выполнять поставленную цель в заданных условиях использования с определённым качеством. Показатели эффективности характеризуют степень приспособленности системы к выполнению поставленных перед нею задач.

Эффективность – выполнение требуемых функций при минимальных затратах ресурсов.

Под ресурсами подразумеваются объём оперативной памяти, время работы центрального процессора, объём внешней памяти, пропускная способность канала.

Сопровождаемость. Требования к сопровождаемости направлены на минимизацию усилий, которые эксплуатирующий персонал тратит на исправление, адаптацию и модернизацию системы. Для их оценки используются различные методики прогнозирования затрат на выполнение типовых процедур сопровождения, основанные на показателях объёма и технологической сложности изделия. Исходным материалом служит программная документация, поэтому её качество является критическим фактором сопровождаемости. Для долгоживущих систем, таких как учётные системы стабильных финансовых учреждений, общая стоимость сопровождения может существенно превышать стоимость разработки.

Мобильность. Мобильность или переносимость изделия характеризует степень свободы в формировании системного окружения, необходимого для её функционирования. Выразить её при помощи количественных показателей затруднительно, так что обычно свойства переносимости описываются в паспорте изделия в виде текста. Оценка переносимости ещё более затрудняется в связи с нестабильностью, динамичностью ассортимента возможных вариантов окружения, обусловленной быстрым прогрессом в сфере информационных технологий.

Основные характеристики и подхарактеристики качества, согласно стандарта ISO/IES 9126, представлены в табл. 3.1

Таблица 3.1

Характеристика	Подхарактеристика	Краткое описание
Функциональные возможности	Пригодность	Способность выполнять все поставленные задачи
Правильность	Правильность выдаваемых результатов
Способность к взаимодействию	Способность взаимодействовать с другими системами (программная независимость)
Согласованность	Соответствие стандартам предметной области
Защищённость	Способность предотвращать несанкционированный доступ
Надёжность	Стабильность	Редкость отказов вследствие внутренних ошибок
Устойчивость к ошибке	Способность функционировать в условиях ошибки
Восстанавливаемость	Способность восстанавливать работу после отказа
Практичность	Понятность	Лёгкость понимания концепции и структуры системы
Обучаемость	Лёгкость изучения системы пользователем
Простота использования	Лёгкость использования системы и управления ею
Эффективность	Характер изменения во времени	Скорость выполнения функции и реакции на запросы
Характер изменения ресурсов	Потребность в ресурсах предоставляемых окружением
Сопровождаемость	Анализируемость	Локализация ошибок, причин отказов, заменяемых частей
Изменяемость	Лёгкость модификации системы, либо окружения
Устойчивость	Отсутствие незапланированных эффектов
Тестируемость	Лёгкость проверки модифицированной системы
Мобильность	Адаптируемость	Удобство настройки на конкретное окружение
Простота внедрения	Лёгкость установки системы в данное окружение
Соответствие	Соответствие соглашениям и стандартам переносимости
Взаимозаменяемость	Лёгкость перехода на данную систему

Количественные показатели