1 Решить задачу Коши для уравнения 
если y=4 при x=1.
Решение.
Заменим 
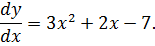
Умножим обе части уравнения на dx:
Интегрируем обе части уравнения:
Чтобы найти частное решение, подставим в общее решение начальные данные:
С=9;
- частное решение.
2Решить уравнение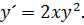 
Решение.
Заменим y´ на 
Умножим обе части на dx:
Разделим обе части уравнения на 
Интегрируем обе части уравнения:
- 
3 Решить уравнение 
Решение.
Умножим обе части уравнения на произведение 
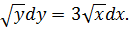
Интегрируем обе части уравнения:
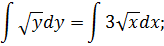
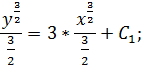
Выразим 
Обозначим 
через C.
4 Решить задачу Коши для уравнения y´+ysinx =0, если y=1 при x=π.
Решение.
Заменим y´на
Умножим обе части уравнения на dx:
dy + ysinxdx=0
Разделим обе части уравнения на y:
Интегрируем обе части уравнения:
- общее решение.
Чтобы найти частное решение, подставим в общее решение начальные данные:
Определим С:
-1+С=0;
С=1.
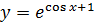- частное решение.
7 Рекомендуемая литература
1. Дадаян А.А. Математика: Учебник – 2-е издание.- М.: Форум: Инфра.-М.2006- 552 с. (Профессиональное образование)
2. Григорьев В. П., Дубинский Ю.А. Элементы высшей математики: Учебник для студентов учреждения среднего профессионального образования. – М.: Издательский центр «Академия», 2004- 320 с.
3. Богомолов Н.В., Самойленко П.И. Математика: учеб. для ссузов – М.: Дрофа, 2010.
4. Пехлецкий И.Д. Математика: Учебник – М.: Министерство, 2001 – 3-4 с.
5. Конспект лекций
6. Настоящая методическая разработка
Приложение А
Варианты индивидуальных заданий
Вариант 1
1. Решить уравнение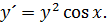 
2. Решить уравнение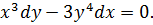 
3. Решить задачу Коши для уравнения 
Вариант 2
1. Решить уравнение 
2. Решить уравнение 
3. Решить задачу Коши для уравнения 
Вариант 3
1. Решить уравнение 
2. Решить уравнение 
3. Решить задачу Коши для уравнения 
Вариант 4
1. Решить уравнение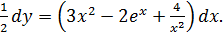 
2. Решить уравнение 
3. Решить задачу Коши для уравнения 
Приложение B
Варианты индивидуальных заданий повышенной сложности
Вариант 1
1. Найти частные решения дифференциальных уравнений:
а) 
, если y = 2 при x = 
;
б) 
, если y = 1/2 при x = 0.
2. Составить уравнение кривой, проходящей через точку М(1; 3) и имеющей угловой коэффициент 
в любой точке касания.
Вариант 2
1. Найти частные решения дифференциальных уравнений:
а) 
, если y = 4 при x = 0;
б) 
, если y = -1 при x = 0.
2. Составить уравнение кривой, проходящей через точку М(5; -2) и имеющей угловой коэффициент 
в любой точке касания.
Вариант 3
1. Найти частные решения дифференциальных уравнений:
а) 
, если y = 0 при x = 0;
б) 
, если y = -1 при x = 0.
2. Составить уравнение кривой, проходящей через точку М(1; 3), если отрезок любой касательной к этой кривой, заключенный между осями координат, делится точкой касания пополам.
Вариант 4
1. Найти частные решения дифференциальных уравнений:
а) 
, если y = 
при x = /3;
б) 
, если y = 0 при x = 1.
2. Составить уравнение кривой, проходящей через точку М(0; 3),если угловой коэффициент касательной в любой точке кривой равен произведению координат точки касания.