Очень часто интересующие нас события являются комбинацией других событий: суммой, произведением, суммой произведений и т.д. Исчисление вероятностей таких сложных (составных) событий проводится по правилам, которые приведены в данном разделе.
5.1. Вероятность суммы несовместных событий
Пусть событие . Вероятность суммы несовместных событий равна сумме вероятностей этих событий. Это утверждение часто называют теоремой сложения вероятностей Пример. Вернемся к рассмотренному в лекции 4 опыту с бросанием двух костей одновременно. Здесь возможны следующие исходы: Первая цифра в паре указывает цифру, выпавшую при бросании первой кости, вторая - при бросании второй. Пусть ?? Чему равны ?? Являются ли события Искомая вероятность будет равна Следствие 1. Если события Следствие 2. Сумма вероятностей противоположных событий равна единице: Вероятность события !! Следствие 2 часто используют при решении задач. Например, найдем вероятность события А, состоящего в том, что наугад названное пятизначное число содержит хотя бы одну четную цифру. 1 способ. Рассмотрим событие А как сумму событий ?? Являются ли события Т.о., вероятность Р(А) найдём по формуле вероятности суммы несовместных событий: 2 способ. Гораздо проще, однако, найти Т.к. чисел с нечетными цифрами а общее число пятизначных чисел то 5.2. Вероятность суммы совместных событий
Рассмотрим вначале сумму двух совместных событий Из рисунка видно, что исходы опыта Вероятность суммы двух совместных событий равна сумме вероятностей этих событий минус вероятность совместного осуществления (произведения) этих событий. Теперь рассмотрим три совместных события Сравнение формул для двух и трех совместных событий позволяет сделать следующий вывод. Вероятность суммы нескольких совместных событий 5.3. Вероятность произведения независимых событий
Два события называются независимыми, если вероятность одного из них не меняется при наступлении другого. Такие события могут наступить при проведении двух независимых опытов. Если число исходов первого опыта Вероятность произведения независимых событий равна произведению вероятностей этих событий: Пример. Задача про любознательного студента Студент разыскивает нужную ему формулу в одном из трёх справочников. Вероятности того, что формула находится в первом, втором и третьем справочниках соответственно равны 0,6; 0,7 и 0,8. Найти вероятности следующих событий: 1) A – формула находится только в одном справочнике; 2) B – формула находится только в двух справочниках; 3) C – формула находится во всех трёх справочниках; 4) D – формулы нет ни в одном справочнике; 5) E – формула находится хотя бы в одном справочнике. Решение. Обозначим – вероятности того, что формула есть соответственно в первом, втором и третьем справочниках, тогда – вероятности противоположных событий, т.е. вероятности того, что формулы нет в этих справочниках. 1) Найдем вероятность события A. Если формула находится только в одном справочнике, то это означает, что: а) либо она находится в первом справочнике, но тогда её нет ни во втором, ни в третьем; б) либо она есть во втором справочнике, но тогда её нет ни в первом, ни в третьем; в) либо она есть в третьем справочнике, но тогда её нет ни в первом, ни во втором. В этих трёх случаях события являются несовместными, а событие А представляет собой сумму произведений элементарных исходов в поиске формулы в каждом из справочников, поэтому 2) Найдем вероятность события B. Если формула находится только в двух справочниках, то так же, как и в предыдущем случае, возможны три варианта её расположения, поэтому при нахождении вероятности события B также будем иметь три слагаемых. 3) При нахождении вероятности события C перемножаем вероятности того, что формулы находятся в соответствующих справочниках (независимые события), 4) а при нахождении вероятности события D — вероятности противоположных событий (независимые между собой события). 5) Вероятность события E найдём двумя способами. 1 способ. Событие «формула есть хотя бы в одном справочнике» заключается в том, что формула есть либо только в одном справочнике, либо только в двух, либо только в трёх. Эти события несовместны, поэтому 2 способ. Событие «формула есть хотя бы в одном справочнике» является противоположным событию «формулы нет ни в одном справочнике». Это означает, что Второй способ предпочтительней при решении задач на нахождение вероятности появления хотя бы одного из событий. ******************************************************************* !!! Домашнее задание (продолжение этой задачи): в условиях данной задачи найти вероятности следующих событий: 6) К – формула находится, по крайней мере, в двух справочниках; 7) М – формула находится не более чем в двух справочниках. ******************************************************************* 5.4. Вероятность произведения зависимых событий
Событие Условной вероятностью Пусть Тогда общим числом возможных исходов для события А будет Вероятность произведения двух зависимых событий равна является суммой событий
является суммой событий 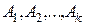 , которым благоприятствуют
, которым благоприятствуют 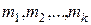 из
из  исходов опыта. Тогда событию
исходов опыта. Тогда событию  благоприятствуют
благоприятствуют 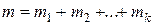 исходов. По классической формуле:
исходов. По классической формуле: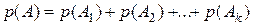 .
.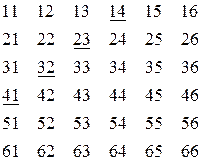
 — выпадение в сумме от 5 до 7 очков. Тогда
— выпадение в сумме от 5 до 7 очков. Тогда 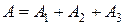 , где
, где  — выпадение в сумме 5 очков,
— выпадение в сумме 5 очков, 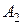 — выпадение в сумме 6 очков,
— выпадение в сумме 6 очков, 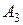 — выпадение в сумме 7 очков. Общее число исходов
— выпадение в сумме 7 очков. Общее число исходов  и значение
и значение 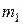 подсчитаны, значения
подсчитаны, значения 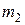 и
и 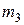 можно подсчитать аналогично.
можно подсчитать аналогично. ,
, 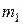 ,
, 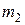 и
и 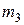 ?
? ,
, 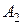 и
и 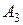 несовместными?
несовместными?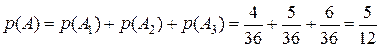 .
.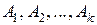 образуют полную группу, то сумма их вероятностей равна 1:
образуют полную группу, то сумма их вероятностей равна 1: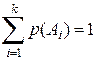 .
.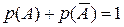 или
или  .
.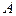 равна 1 минус вероятность события, противоположного
равна 1 минус вероятность события, противоположного 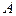 .
. ,
, 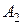 ,
, 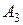 ,
, 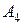 и
и 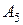 .
. , где
, где — названное число содержит 1 четную цифру;
— названное число содержит 1 четную цифру;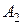 — названное число содержит 2 четные цифры;
— названное число содержит 2 четные цифры;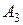 — названное число содержит 3 четные цифры;
— названное число содержит 3 четные цифры;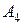 — названное число содержит 4 четные цифры;
— названное число содержит 4 четные цифры;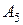 — названное число содержит 5 четных цифр;
— названное число содержит 5 четных цифр; ,
, 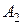 ,
, 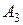 ,
, 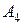 и
и 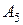 несовместными?
несовместными? .
.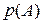 , вычислив вероятность противоположного события
, вычислив вероятность противоположного события 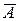 – в названном числе не содержится ни одной четн ой цифры.
– в названном числе не содержится ни одной четн ой цифры.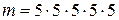 (по правилу произведения для комбинаторных соединений, поскольку выбираем из 1,3,5,7,9, а цифры в числе могут повторяться),
(по правилу произведения для комбинаторных соединений, поскольку выбираем из 1,3,5,7,9, а цифры в числе могут повторяться),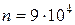 (??-как сосчитали?),
(??-как сосчитали?),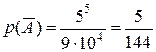 ; тогда по формуле вероятности для противоположных событий получим
; тогда по формуле вероятности для противоположных событий получим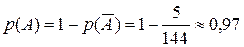 .
.
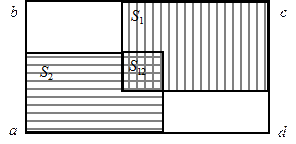
 и
и 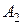 . Представим общее число исходов
. Представим общее число исходов  площадью
площадью 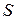 прямоугольника
прямоугольника  , исходы
, исходы 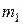 , благоприятствующие
, благоприятствующие  — площадью
— площадью 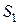 , исходы
, исходы 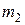 , благоприятствующие событию
, благоприятствующие событию 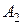 — площадью
— площадью 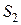 . Площадь
. Площадь 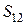 соответствует исходам
соответствует исходам 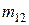 , благоприятствующим и событию
, благоприятствующим и событию  и событию
и событию 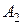 .
.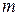 , благоприятствующие событию
, благоприятствующие событию 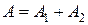 , представлены отмеченной штриховкой площадью
, представлены отмеченной штриховкой площадью  . Воспользовавшись геометрическим способом вычисления вероятности, можем найти
. Воспользовавшись геометрическим способом вычисления вероятности, можем найти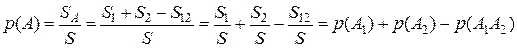 .
.
 ,
, 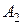 ,
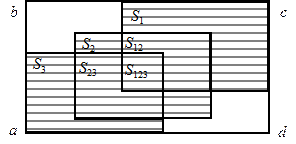
, 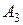 . Как и в предыдущем случае будем считать, что площадь прямоугольника
. Как и в предыдущем случае будем считать, что площадь прямоугольника 
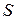 соответствует всем исходам опыта,
соответствует всем исходам опыта, 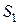 — исходам, благоприятствующим событию
— исходам, благоприятствующим событию  ,
, 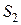 — исходам, благоприятствующим событию
— исходам, благоприятствующим событию 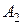 ,
, 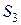 — исходам, благоприятствующим
— исходам, благоприятствующим 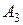 ,
, 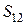 — и событию
— и событию  , и событию
, и событию 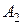 ,
, 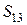 — и событию
— и событию  , и событию
, и событию 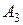 ,
, 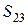 — и
— и 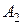 , и
, и 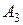 ;
;  — всем трем событиям одновременно. Событию
— всем трем событиям одновременно. Событию 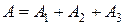 соответствует площадь, отмеченная штриховкой. Обращаясь вновь к геометрическому определению вероятности, найдем
соответствует площадь, отмеченная штриховкой. Обращаясь вновь к геометрическому определению вероятности, найдем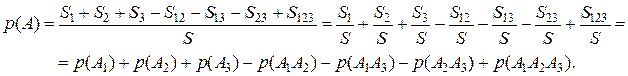
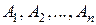 равна сумме вероятностей этих событий минус вероятность всех возможных произведений четного числа событий плюс вероятность всевозможных произведений нечетного числа событий.
равна сумме вероятностей этих событий минус вероятность всех возможных произведений четного числа событий плюс вероятность всевозможных произведений нечетного числа событий.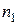 , а число исходов второго
, а число исходов второго 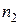 , то общее число исходов при одновременном проведении двух опытов
, то общее число исходов при одновременном проведении двух опытов 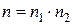 . Если
. Если 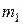 исходов благоприятствуют событию
исходов благоприятствуют событию  , а
, а 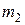 — событию
— событию 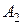 , то общее число способов осуществить пару событий
, то общее число способов осуществить пару событий 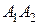 равно
равно 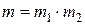 , тогда
, тогда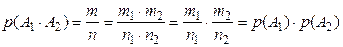 .
.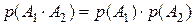 .
.
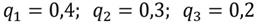


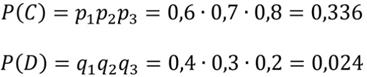

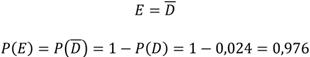
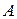 называется зависимым от события
называется зависимым от события 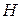 , если вероятность события
, если вероятность события 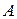 меняется при наступлении события
меняется при наступлении события 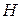 .
.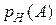 события
события 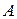 относительно события
относительно события 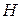 называется вероятность события
называется вероятность события 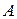 , вычисленная в предположении, что событие
, вычисленная в предположении, что событие 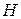 наступило.
наступило.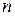 - общее число возможных исходов опыта, из них
- общее число возможных исходов опыта, из них 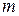 исходов благоприятствуют событию Н. Предположим, что событие Н произошло. По определению:
исходов благоприятствуют событию Н. Предположим, что событие Н произошло. По определению:  .
.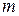 . Пусть
. Пусть  из них благоприятствуют событию А, а значит и событию АН. Тогда вероятность одновременного наступления событий и А, и Н, т.е. их произведения, равна
из них благоприятствуют событию А, а значит и событию АН. Тогда вероятность одновременного наступления событий и А, и Н, т.е. их произведения, равна 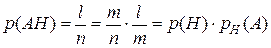 .
.