Пример. Тема: «Функция у=ах2, её график и свойства». (алгебра 8 класс)
Учащимся предлагается построить попарно графики функций у=2х2 и
у= -2х2 и, опираясь на непосредственное изображение графиков, заполнить таблицу (выполнить построение в Excel):
| Свойства функции | у=2х2 (у=ах2, а>0) | у= -2х2 (у=ах2, а<0) |
| 1.Область определения функции | ||
| 2.Область значения функции | ||
| 3.Нули функции | ||
| 4.График функции и его расположение | ||
| 5.Промежутки возрастания и убывания функции |
После заполнения таблицы учащиеся делают окончательные выводы и формулируют основные свойства.
Приложение 5.
Создание проблемных ситуаций через решение задач на внимание и сравнение.
Тема: «Сумма углов треугольника» (геометрия 7 класс)
Учитель читает условие задачи, ученики анализируют его и выявляют ошибки, тем самым мы можем проверить учеников на внимательность. В данных задачах следует вспомнить теорему о сумме углов треугольника, полагаясь на данную теорему, мы придем к выводу, что не все условия задач поставлены корректно, тем самым некоторые треугольники не существуют.
Пример 1. Построить треугольник по трем заданным углам




Учащиеся, вооружившись линейкой и транспортиром, начинают строить треугольники. По окончании уже можно выдвинуть предположение о сумме внутренних углов треугольника. Здесь уместен провокационный вопрос: «В каком треугольнике, по вашему мнению, сумма внутренних углов больше, в остроугольном или тупоугольном?» Практика показывает, что в каждом классе найдутся несколько человек, которые, зная, что тупой угол всегда больше острого, по аналогии скажут, что сумма внутренних углов тупоугольного треугольника, больше, чем остроугольного. Я предлагаю им на практике проверить свое утверждение.
Пример 2. Два угла треугольника равны 121º и 59º. Найти величину третьего угла.
Пример 3. В треугольнике АВС найдите неизвестные углы,
если  на
на  больше
больше 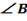 , а
, а  .
.
Пример 4. Дан треугольник АВС, где  . Найти
. Найти  .
.
Приложение 6.
Создание проблемных ситуаций через противоречие нового материала старому, уже известному.
Пример 1. Тема: «Формулы сокращённого умножения» (алгебра 7 класс)
Учитель дает задание, пытаясь запутать учеников. Вычислите:
(3٠4)2 =32٠42=9٠16=144
(5٠6)2 =52٠62=25٠36=900
(8:2)2 =82:22=64:4=16
(3:9)2 =32:92= =
(5+6)2 =52+62=25+36=61
Решим последний пример, соблюдая порядок действий в вычислениях: (5+6)2 =112=121
Имеем: (5+6)2≠52+62
Почему в итоге получились разные результаты? И какой из результатов верный?
Ученики обращают внимание на знак в последнем примере и понимают, что данный пример решается по-другому (применяя формулу для квадрата суммы).
Приложение 7.
Создание проблемных ситуаций через различные способы решения одной задачи.
Тема: «Распределительный закон умножения относительно сложения» (математика 5 класс)
На данном уроке учащимся предлагается решить следующие задачи:
Задача 1. В школьном саду посажены фруктовые деревья в 10 рядов. В каждом ряду посажено по 5 груш и по 7 яблонь. Сколько всего деревьев посажено в саду?
Решение.
1 способ. 2 способ.
(7 + 5) ٠10 = 120 7 ٠10 + 5 ٠10 = 120
Ответ: 120 деревьев.
Задача 2. Две автомашины одновременно выехали навстречу друг другу из двух пунктов. Скорость первой автомашины 80 км в час, скорость второй 60 км в час. Через 3 часа автомашины встретились. Какое расстояние между пунктами, из которых выехали автомашины?
Решение.
1 способ. 2 способ.
(80 + 60) ٠3 = 420 80 ٠ 3 + 60 ٠3 = 420
Ответ: 420 км
В результате такого сравнения учащиеся пришли к следующим выводам:
• 1-й способ решения всех задач одинаков, 2-й – тоже.
• выражения, полученные при решении задач отличаются друг от друга только числовыми данными;
• выражения, полученные при решении задачи №1 и № 2 1-м и 2-м способами, отличаются друг от друга числом арифметических действий и порядком действий;
• числовые значения выражений, полученные при решении задачи №1 2-мя способами, одинаковы, а, значит, можно сделать такую запись:
(7 + 5) ٠10 = 7 ٠10 + 5 ٠10.
(80 + 60) ٠3 = 80 ٠3 + 60 ٠3.
Далее предлагается ученикам заменить одинаковые цифры в полученных выражениях одинаковыми буквами. В результате получены два одинаковых выражения, а именно: (а + в) ٠с = ас + вс.
Ученики с помощью учителя формулируют этот закон словесно и на примерах новый закон умножения: распределительный закон умножения относительно сложения.
Убеждаются в целесообразности усвоения и запоминания этого закона: он облегчает вычисления.
Приложение 8.
Создание проблемных ситуаций через выполнение небольших исследовательских заданий.
Пример. Тема «Длина окружности» (математика 5 класс)
Ещё древние греки находили длину окружности по формуле С=πd, d - это диаметр окружности.
Вопрос: а что же такое?
Работаем в парах, выполняя необходимые измерения.
1.Опоясать стакан ниткой, распрямить нитку, длина нитки примерно равна длине окружности стакана. Чтобы получить более точный результат, нужно это проделать несколько раз. Занесите данные в следующую таблицу.
| № опыта | Длина окружности | Диаметр | |
| С 1 | d 1 | ||
| С 2 | d 2 | ||
| 3… | С 3… | d 3 |
2.Измерьте диаметр стакана линейкой. Данные занесите в таблицу.
3.Найдите значение π, как неизвестного множителя. Можно пользоваться калькулятором
4.Каждой паре занести вычисленное значение π в таблицу.
π- это бесконечная дробь, современные машины могут определить до миллиона знаков после запятой.
π≈3,1415926…
Для того, чтобы легче запомнить цифры надо запомнить считалку: «Надо только постараться и запомнить всё как есть: 3, 14, 15, 92 и 6».
В дальнейшей работе мы будем использовать значение π ≈3,14.
Исследование проведено. На уроке, кроме исследовательской работы удачно использовалась работа в парах. Сотрудничество и взаимопомощь принесли желаемый результат. Проблема решена.