Статистическая обработка результатов эксперимента. Случайные погрешности результатов наблюдений интервалов времени
Цель работы: ознакомление со статистической обработкой результатов измерений и оценкой случайной погрешности измерений интервалов времени
Теоретическое введение
Рассмотрим основные положения теории случайных погрешностей. Она базируется на двух главных предположениях, подтверждаемых опытом:
1. При большом числе наблюдений одинаково часто встречаются погрешности одинаковой величины, но разного знака.
2. Вероятность появления погрешности уменьшается с ростом величины погрешности.
Закономерности, связанные со случайными величинами, изучаются теорией вероятности. Будем использовать частотное определение вероятности. Это определение связано с представлениями о зависимости между вероятностью и частотой появления события, принятыми в повседневной практике.
Обозначим через 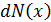 число измерений, для которых физическая величина
число измерений, для которых физическая величина 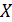 попала в интервал значений между
попала в интервал значений между 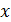 и
и 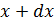 , через
, через 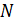 – полное число измерений. Соответственно следует говорить не о точном (истинном) значении величины
– полное число измерений. Соответственно следует говорить не о точном (истинном) значении величины 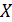 , а некотором интервале ее значений, то есть о вероятности того, что величина
, а некотором интервале ее значений, то есть о вероятности того, что величина 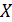 имеет значения, лежащие в интервале между
имеет значения, лежащие в интервале между 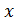 и
и 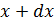 . Эту вероятность обозначают
. Эту вероятность обозначают 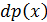
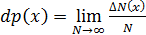 (2.1)
(2.1)
Очевидно, что вероятность 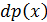 пропорциональна величине интервала
пропорциональна величине интервала 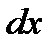 . Поэтому удобно представить
. Поэтому удобно представить 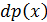 в виде
в виде
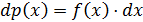 , (2.2)
, (2.2)
где коэффициент пропорциональности 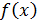 в общем случае также зависит от x. Значение функции
в общем случае также зависит от x. Значение функции 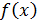 численно равно вероятности того, что величина
численно равно вероятности того, что величина 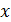 лежит в “единичном” интервале вблизи заданногоx.
лежит в “единичном” интервале вблизи заданногоx. 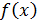 называется плотностью вероятности или функцией распределения.
называется плотностью вероятности или функцией распределения.
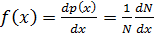 (2.3)
(2.3)
|
|
Теперь с помощью функции распределения мы хотя и не можем указать точно, чему равно истинное значение 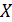 измеренной величины, но можем найти, с какой вероятностью p величина x окажется в интервале значений
измеренной величины, но можем найти, с какой вероятностью p величина x окажется в интервале значений  . Эта область значений называется доверительным интервалом, а связанная с ним величина p – доверительной вероятностью.
. Эта область значений называется доверительным интервалом, а связанная с ним величина p – доверительной вероятностью.
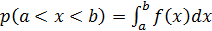 (2.4)
(2.4)
Пусть измерение состоит из 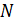 независимых повторных наблюдений величины
независимых повторных наблюдений величины 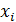 (i =1, 2, 3, ….,
(i =1, 2, 3, …., 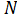 ). Тогда среднее арифметическое
). Тогда среднее арифметическое
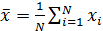 (2.5)
(2.5)
Примечание. Приняты обозначения для среднего арифметического значения: 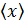 , или
, или 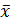 , или
, или 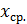 .
.
При  среднее арифметическое совпадает с истинным значением X.
среднее арифметическое совпадает с истинным значением X.
Значения 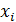 определённым образом группируются относительно истинного значения X. Мерой отклонения значения
определённым образом группируются относительно истинного значения X. Мерой отклонения значения 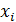 в совокупности измерений служит среднеквадратичное отклонение отдельного измерения
в совокупности измерений служит среднеквадратичное отклонение отдельного измерения 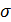 .
.
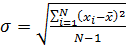 (2.6)
(2.6)
Квадрат этой величины 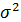 называется дисперсией. Величины
называется дисперсией. Величины 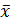 ,
, 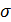 ,
, 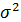 определяют плотность распределения результатов наблюдения (или плотность вероятности
определяют плотность распределения результатов наблюдения (или плотность вероятности 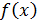 ). Обычно предполагают, что плотность вероятности подчиняется нормальному закону распределения и описывается функцией распределения Гаусса:
). Обычно предполагают, что плотность вероятности подчиняется нормальному закону распределения и описывается функцией распределения Гаусса:
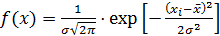 (2.7)
(2.7)
| Рис. 2.1. Функция распределения Гаусса |
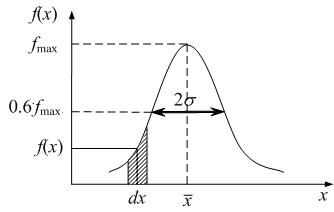 Вид функции Гаусса показан на рис.2.1.
Вид функции Гаусса показан на рис.2.1.
Произведение 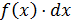 равно вероятности получения результата наблюдения, попадающего в промежуток [
равно вероятности получения результата наблюдения, попадающего в промежуток [ 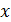 ,
, 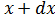 ]. Геометрически эта вероятность выражается заштрихованной площадкой на рисунке. Очевидно, что полная площадь под кривой
]. Геометрически эта вероятность выражается заштрихованной площадкой на рисунке. Очевидно, что полная площадь под кривой 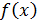 равна 1 (или 100%). На практике выполняют ограниченное число измерений. В этом случае все полученные измерения величины
равна 1 (или 100%). На практике выполняют ограниченное число измерений. В этом случае все полученные измерения величины 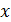 представляют выборку, а
представляют выборку, а 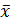 , определённое по (2.5), называется средним арифметическим. Оно не совпадает с истинным значением величины
, определённое по (2.5), называется средним арифметическим. Оно не совпадает с истинным значением величины 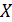 . Поэтому при проведении конечного числа измерений (а на практике только это и возможно!) не удается установить истинное значение
. Поэтому при проведении конечного числа измерений (а на практике только это и возможно!) не удается установить истинное значение 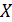 . Можно лишь указать границы
. Можно лишь указать границы 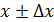 значений, в которых лежит основная часть измерений. Так, например, если
значений, в которых лежит основная часть измерений. Так, например, если 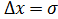 , то
, то 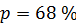 , если
, если 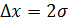 , то
, то 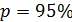 , если
, если 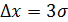 , то
, то  .
.
|
|
Интервал 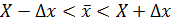 и вероятность
и вероятность 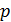 называют доверительными. На практике величина
называют доверительными. На практике величина 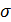 (и дисперсия) неизвестна (количество измерений ограничено). Поэтому для оценки используют её приближенное значение, называемое среднеквадратичной погрешностью (среднеквадратичное отклонение среднего значения
(и дисперсия) неизвестна (количество измерений ограничено). Поэтому для оценки используют её приближенное значение, называемое среднеквадратичной погрешностью (среднеквадратичное отклонение среднего значения 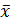 ):
):
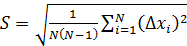 (2.8)
(2.8)
Распределение Гаусса позволяет достаточно надёжно определить случайные погрешности измерений при большом числе измерений. В инженерной практике (при 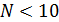 ) вместо распределения Гаусса следует использовать распределение Стьюдента. В этом случае можно показать, что для каждой доверительной вероятности
) вместо распределения Гаусса следует использовать распределение Стьюдента. В этом случае можно показать, что для каждой доверительной вероятности 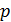 можно найти такое число
можно найти такое число 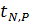 , называемое коэффициентом Стьюдента, что погрешность прямых измерений может быть оценена следующим образом:
, называемое коэффициентом Стьюдента, что погрешность прямых измерений может быть оценена следующим образом:
 (2.9)
(2.9)
Величину 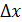 ещё называют доверительной случайной погрешностью результата измерения, а вероятность
ещё называют доверительной случайной погрешностью результата измерения, а вероятность 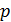 – надежностью (доверительной вероятностью) результата. Зная число N измерений в опыте и задавая надежность
– надежностью (доверительной вероятностью) результата. Зная число N измерений в опыте и задавая надежность 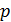 (обычно принимают
(обычно принимают 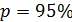 ), по таблице в приложении находят значение коэффициента Стьюдента.
), по таблице в приложении находят значение коэффициента Стьюдента.
Окончательно результаты измерения можно записать в виде:
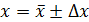 , (2.10)
, (2.10)
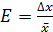 . (2.11)
. (2.11)
Методика измерений
Работа выполняется одновременно всей подгруппой, разбитой на бригады по 2 человека. Преподаватель запускает метроном (на каждом занятии может быть задана своя частота колебаний метронома), и каждая бригада получает конкретное задание: измерить длительность двух качаний метронома, другой бригаде – трёх качаний и т. д., то есть каждая бригада будет измерять свой временной интервал. Каждое измерение выполняется вдвоем: один студент дает команды на включение и выключение секундомера (ориентируясь на метроном или показания часов), а другой осуществляет запуск секундомера и его остановку и регистрирует результат в таблице. При этом важно, чтобы первый студент не знал результатов каждого конкретного измерения (требование независимости измерений).
|
|
Полученные результаты используются для достижения двух целей: одна – научиться выполнять оценку погрешности прямых измерений, другая – убедиться в действии закона нормального распределения при проведении измерений, сопровождающихся случайной погрешностью.
Порядок выполнения работы
Задание 1. Определение погрешности прямых измерений.
1. Бригада выполняет 50 измерений указанного преподавателем интервала времени 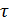 . Результаты занесите в таблицу 2.1 (столбец 2).
. Результаты занесите в таблицу 2.1 (столбец 2).
2. По формуле 2.5 вычислите среднее арифметическое 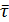 .
.
3. Найдите отклонения каждого измерения от среднего 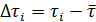 (столбец 3) и
(столбец 3) и 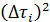 (столбец 4).
(столбец 4).
4. По формуле 2.8 вычислите выборочное среднее квадратическое отклонение 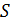 .
.
5. По таблице в приложении найти коэффициент Стьюдента 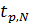 (для
(для  ,
, 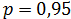 ).
).
6. Найдите доверительный интервал 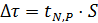 .
.
7. Запишите результат измерений промежутка времени в виде: 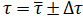 .
.
8. Определите относительную погрешность 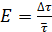 .
.
Таблица 2.1. Результаты измерений
| № п/п | 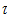
| 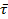
| 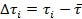
| 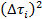
| 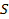
| 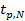
| 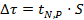
| 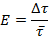
|
| с | с | с | с2 | с | - | с | - | |
| … | ||||||||
Задание 2. Построение кривой распределения.
1. Выберите из результатов измерений наибольшее 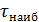 и наименьшее
и наименьшее 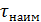 значения интервалов времени. Определите промежуток изменений интервалов времени
значения интервалов времени. Определите промежуток изменений интервалов времени 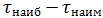 .
.
2. Разбейте весь промежуток на 10 равных частей (зон) 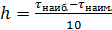
3. Заполните столбцы таблицы 2.2:
подставьте конкретные числа, характеризующие границы зон (столбец 2);
подсчитайте количество значений n измеренных интервалов времени t, попадающих в данную зону (столбец 3);
подсчитайте относительное число измеренных интервалов времени, попадающих в каждую зону,  (столбец 4), и значение функции распределения
(столбец 4), и значение функции распределения 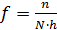 (столбец 5).
(столбец 5).
4. Постройте гистограмму (см. рис. 2.2). Построение выполняйте на миллиметровке! Для этого по оси абсцисс отложите значения измеренных интервалов времени, укажите на оси t наименьшее и наибольшее значения 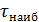 и
и 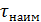 , проведите разбиение на 10 зон шириной
, проведите разбиение на 10 зон шириной 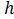 . На каждой зоне постройте прямоугольник, высота которого равна относительному числу измеренных интервалов времени
. На каждой зоне постройте прямоугольник, высота которого равна относительному числу измеренных интервалов времени 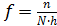 . Другими словами, гистограмма отражает связь между соответствующими значениями 5-го и 2-го столбцов таблицы 2.2.
. Другими словами, гистограмма отражает связь между соответствующими значениями 5-го и 2-го столбцов таблицы 2.2.
Таблица 2.2
Данные для построения гистограммы
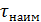
| 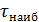
| 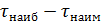
| 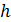
| 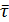
| 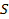
| 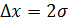
| |||||
| № зоны k | Границы зоны | 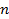
| 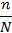
| 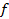
| 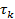
| 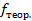
| |||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |||||
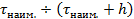
| |||||||||||
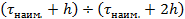
| |||||||||||
| … | … | ||||||||||
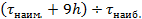
| |||||||||||
| Контроль | Итого | 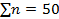
| 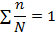
| ||||||||
5. Нарисуйте кривую плотности распределения результатов измерений. Для этого рассчитайте координаты 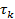 середины каждой зоны с номером k (столбец 6 таблицы 2.2), отметьте точками середины вершин построенных прямоугольников и постройте по этим точкам плавную кривую (см. рис. 2.2).
середины каждой зоны с номером k (столбец 6 таблицы 2.2), отметьте точками середины вершин построенных прямоугольников и постройте по этим точкам плавную кривую (см. рис. 2.2).
6. Найдите среднее арифметическое 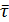 .
.
7. Найдите среднеквадратическое отклонение 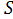 .
.
8. Найдите по графику доверительный интервал для надежности 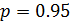 . Он примерно равен
. Он примерно равен 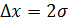 .
.
9. Рассчитайте теоретические значения 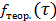 функции распределения (столбец 7) по формуле (2.12) в точках
функции распределения (столбец 7) по формуле (2.12) в точках 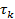 , соответствующих середине каждой зоны; постройте график функции
, соответствующих середине каждой зоны; постройте график функции 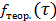 (столбцы 6 и 7); сравните его с экспериментальным графиком.
(столбцы 6 и 7); сравните его с экспериментальным графиком.
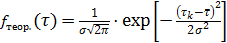 (2.12)
(2.12)
10. Сделайте выводы.
| τ |
| τнаиб |
2 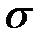
|
| f max |
| 0.6ּ f max |
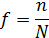
|
| τнаим |
| h |
| Рис. 2.2. Гистограмма распределения результатов измерений интервалов времени |
| τk |
Контрольные вопросы
1. Что понимается в физике под измерением? Приведите примеры.
2. Виды измерений.
3. Почему при проведении измерений появляются погрешности? Можно ли выполнить измерения "точно"?
4. Какие предположения лежат в основе теории случайных погрешностей?
5. Сколько нужно выполнить измерений, чтобы можно было воспользоваться законом нормального распределения?
6. Что такое "доверительный интервал", "надежность"?
7. Как на практике находят доверительный интервал при заданной надежности? Что такое коэффициент Стьюдента?
8. Как по виду функции Гаусса (по графику) определить дисперсию?
9. Что такое "гистограмма"?
10. Подтверждается ли в Вашей работе предположение о том, что результаты измерений подчиняются закону нормального распределения? Почему?