Задача 10. Составьте блок-схему алгоритма вычисления суммы n-го количества слагаемых  при различных значениях параметра суммирования x, где общий член суммы имеет вид:
при различных значениях параметра суммирования x, где общий член суммы имеет вид:
0) 
| 1) 
| 2) 
| 3) 
| 4) 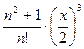
|
5) 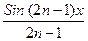
| 6) 
| 7) 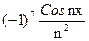
| 8) 
| 9) 
|
Элементы теории конечных автоматов
Задача 11.
0. Построить таблицу автомата, представляющего двоичный сумматор последовательного действия.
1. Построить таблицу автомата, представляющего троичный сумматор последовательного действия.
2. Построить таблицу автомата, представляющего четверичный сумматор последовательного действия.
3. Построить диаграмму автомата, представляющего двоичный сумматор последовательного действия.
4. Построить диаграмму автомата, представляющего троичный сумматор последовательного действия.
5. Построить в виде последовательности четверок конечный автомат, выдающий на выходе символ ”&” всякий раз, когда во входной двоичной последовательности встречается последовательность 3005.
6. Задать автомат в виде последовательности четверок, представляющий двоичный сумматор последовательного действия.
7. Задать автомат в виде последовательности четверок, представляющий троичный сумматор последовательного действия
8. Построить в виде последовательности четверок конечный автомат, выдающий на выходе символ ”*” всякий раз, когда во входной двоичной последовательности встречается последовательность 1200.
9. Построить конечный автомат, выдающий на выходе символ ”?” всякий раз, когда во входной двоичной последовательности встречается последовательность 0000.
Контрольная работа выполняется по предложенным задачам и включает 11 задач. Вариант в задачах выбирается по таблице распределения задач на пересечении столбца с номером задачи и строки с соответствующей по счету буквой в фамилии, имени и отчестве.
Требования к оформлению контрольной работы:
- контрольную работу оформить в отдельной тетради в клетку;
- каждое задание оформляется, начиная с новой страницы;
- условия задач полностью переписываются;
- на титульном листе указывается дисциплина, курс, учебная группа, фамилия, имя, отчество и шифр задач, состоящий из 11 цифр, где каждая цифра - номер варианта соответствующей задачи, определенный по таблице.
Например,
Иванов Петр Сидорович имеет шифр 84912009310.
ТАБЛИЦА РАСПРЕДЕЛЕНИЯ ЗАДАЧ
| ЗАДАЧИ | |||||||||||
| Первая буква фамилии | Вторая буква фамилии | Третья буква фамилии | Первая буква имени | Вторая буква имени | Третья буква имени | Первая буква отчества | Вторая буква отчества | Третья буква отчества | Четвертая буква отчества | Последняя буква отчества | |
| А | |||||||||||
| Б | |||||||||||
| В | |||||||||||
| Г | |||||||||||
| Д | |||||||||||
| Е, Ё | |||||||||||
| Ж | |||||||||||
| З | |||||||||||
| И, Й | |||||||||||
| К | |||||||||||
| Л | |||||||||||
| М | |||||||||||
| Н | |||||||||||
| О | |||||||||||
| П | |||||||||||
| Р | |||||||||||
| С | |||||||||||
| Т | |||||||||||
| У | |||||||||||
| Ф | |||||||||||
| Х | |||||||||||
| Ц, Ч | |||||||||||
| Ш, Щ, Ь, Ъ,Ы | |||||||||||
| Э,Ю,Я |
ЛИТЕРАТУРА:
Основная
1. Шмырин А.М. Лекции по дискретной математике и математической логике: учеб. пособие / И.А. Седых, А.М. Шмырин.— Липецк: ЛГТУ, 2014.— ISBN 978-5-88247-714-0
2. Веретенников, Б.М. Дискретная математика. Ч. I: учеб. пособие / В.И. Белоусова, Б.М. Веретенников.— Екатеринбург: Издательство Уральского университета, 2014.— ISBN 978-5-7996-1199-6 (Ч. 1).— ISBN 978-5-7996-1195-8
3. Хаггарти Р. Дискретная математика для программистов [Электронный ресурс]: учебное пособие/ Хаггарти Р.— Электрон. текстовые данные.— М.: Техносфера, 2012.— 400 c.— Режим доступа: https://www.iprbookshop.ru/12723.— ЭБС «IPRbooks», по паролю
4. Лихтарников Л.М., Сукачева Т.Г. Математическая логика. Курс лекций. Задачник-практикум и решения. -СПб.: Изд-во "Лань", 1998. -285 с.
5. Карпов В.Г., Мощенский В.А. Математическая логика и дискретная математика. –Минск: Вышейшая школа, 1977. –254 с.
6. Шоломов Л.А. Основы теории дискретных логических и вычислительных устройств. -М.: Наука, 1980. -399с.
7. Н.Г.Колесников Математические и логические основы информатики.- г.Краснодар Куб.ГАУ –2000г.,- 224с.
8. В.А.Трахтенборт Алгоритмы и вычислительные автоматы. –М., «Советское радио»,1974г.,-200с.
Дополнительная
1. Калбертсон Дж. Т. Математика и логика цифровых устройств. -М.: Прсвещение, 1965. -267 с.
2. Маслюков О.А. Вычислительная техника и программирование. -М.: Высшая школа, 1993. -208 с.
3. Никольская И.Л. Математическая логика. -М.: Высшая школа, 1981. -127 с.
4. С.В. Яблонский. Введение в дискретную математику. –М.:Наука, 1999. –272 с.