частицы, вызывающей ядерную реакцию

 

где - масса покоя налетающей

частицы,

- масса покоящейся частицы,

 

Примеры решения задач.

Пример 45. Электрон в атоме водорода перешел с четвертого энергетического уровня на второй. Определить энергию испущенного при этом фотона.

Решение. Для определения энергии фотона воспользуемся формулой для водородоподобных ионов:

 

, (1)

где λ – длина волны; R – постоянная Ридберга; Z – заряд ядра в относительных единицах (при Z=1 формула переходит в серийную формулу для водорода); n₁ – номер орбиты, на которую перешел электрон;n₂ – номер орбиты, с которой перешел электрон (n_{1 и} n₂ - главные квантовые числа).

Энергия фотона ε выражается формулой

 

, (2)

Поэтому, умножив обе части равенства (1) на hc, получим выражение для энергии фотона

.

Так как Rhc есть энергия ионизации Е_i атома водорода, то

 

.

Вычисление выполним во внесистемных единицах:

Е_i =13,6 эВ; Z=1; n₁=2; n₂=4:

Пример 46. При соударении α-частицы с ядром бора произошла ядерная реакция, в результате которой образовалось два новых ядра. Одним из этих ядер было ядро атома водорода Определить порядковый номер и массовое число второго ядра, дать символическую запись ядерной реакции и определить ее энергетический эффект.

Решение. Обозначим неизвестное ядро символом 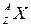. Так как α-частица представляет собой ядро гелия , запись реакции имеет вид

Применив закон сохранения числа нуклонов, полу­чим уравнение 4+10= 1 +А, откуда А = 13. Применив закон сохранения заряда, получим уравнение 2 + 5 = 1+Z, откуда Z = 6. Следовательно, неизвестное ядро является ядром атома изотопа углерода .

Теперь можем записать реакцию в окончательном виде:

Энергетический эффект Q ядерной реакции определя­ется по формуле

Q=931[(m_He + m_B)-(m_H + m_C)].

Здесь в первых круглых скобках указаны массы исходных ядер, во вторых скобках — массы ядер — про­дуктов реакции. При числовых подсчетах по этой форму­ле массы ядер заменяют массами нейтральных атомов. Возможность такой замены вытекает из следующих соображений.

Число электронов в электронной оболочке нейтраль­ного атома равно его зарядовому числу Z. Сумма заря­довых чисел исходных ядер равна сумме зарядовых чисел ядер — продуктов реакции. Следовательно, электронные оболочки ядер гелия и бора содержат вместе столько же электронов, сколько их содержат электронные оболочки ядер углерода и водорода.

Очевидно, что при вычитании суммы масс нейтраль­ных атомов углерода и водорода из суммы масс атомов гелия и бора массы электронов выпадут, и мы получим тот же результат, как если бы брали массы ядер. Подста­вив массы атомов (см. табл. 10 Приложения) в расчет­ную формулу, получим

Q=931(4,00260+10,01294)-(1,00783+13,00335) МэВ = = 4,06 МэВ.

Пример 47. Вычислить дефект массы и энергию связи ядра

Решение. Масса ядра всегда меньше суммы масс свободных (находящая вне ядра) протонов и нейтро­нов, из которых ядро образовалось. Дефект массы ядра Δm и есть разность между суммой масс свободных нукло­нов (протонов и нейтронов) и массой ядра, т. е.

Δm =Zm_p+(A-Z)m_n-m_я (1)

где Z — атомный номер (число протонов в ядре); А — массовое число (число нуклонов, составляющих ядро); m_р, m_n, m_я — соответственно массы протона, нейтрона и ядра.

В справочных таблицах всегда даются массы нейт­ральных атомов, но не ядер, поэтому формулу (1) целе­сообразно преобразовать так, чтобы в нее входила мас­са m_янейтрального атома. Можно считать, что масса нейтрального атома равна сумме масс ядра и электронов, составляющих электронную оболочку атома: m_а=m_я + Zm_e, откуда

M_я=m_а – Zm_e (2)

Выразив в равенстве (1) массу ядра по формуле (2), получаем

Δm =Zm_p+(A-Z)m_n- m_а + Zm_e, или Δm=Z(m_p +m_e)+(А –Z) m_n - m_а

Замечая, что m_р-m_е = m_н, где m_н ­ - масса водорода, окончательно находим

Δm=Zm_н+(А-Z) m_n - m_а . (3)

 

Подставив в выражение (3) числовые значения масс (см. табл. 12 и 13 Приложения), получим

Δm = [3·1,00783+(7-3) · 1,00867-7·0,1601] а. е. м =0,04216 а.е. м.

В соответствии с законом пропорциональности массы и энергии

Е =Δ тс²,(4)

где с - скорость света в вакууме.

Коэффициент пропорциональности с² может быть выражен двояко:

с²= 9·10¹⁶ м²/с², или с² =ΔЕ/ Δm=9·10¹⁶Дж/кг

Если вычислить энергию связи, пользуясь внесистем­ными единицами, то с² = 931 МэВ/а. е. м. С учетом этого формула (4) примет вид

Е=931Δm(МэВ). (5)

Подставив найденное значение дефекта массы ядра в формулу (5), получим

Е = 93 1 • 0,042 1 6 МэВ = 39,2 МэВ.

Примечание. Термин «дефект массы» часто применяют в другом смысле: дефектом массы Δm называют разность между массой нейт­рального атома данного изотопа и его массовым числом А: Δ = m_а — А. Эта величина особого физического смысла не имеет, но ее использова­ние позволяет в ряде случаев значительно упростить вычисления. В на­стоящем пособии всюду имеется в виду дефект массы Δmα, определяе­мый формулой (1).

 

Пример 48. Определить начальную активность А₀ радиоактивного препарата магния 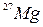массой m=0,2 мкг, а также его активность А через время t=6 ч. Период полураспада магния считать известным.

Решение. Активность А изотопа характеризует скорость радиоактивного распада и определяется отношением числа dN ядер, распавшихся за интервал времени dt, к этому интервалу:

(1)

Знак «-» показывает, что число N радиоактивных ядер с течением вр6емени убывает.

Для того чтобы найти , воспользуемся законом радиоактивного распада:

, (2)

где N- число радиоактивных ядер, содержащихся в изотопе, в момент времени t; N₀- число радиоактивных ядер в момент времени, принятый за начальный (t=0);λ- постоянная радиоактивного распада.

Продифференцируем выражение (2) по времени:

(3).

Исключим из формул (1) и (2) dN/dt, находим активность препарата в момент времени t:

(4)

Начальную активность А₀ препарата получим при t=0:

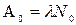(5)

Постоянная полураспада λ связана с периодом полураспада Т_1/2 соотношением

(6)

Число N₀ радиоактивных ядер, содержащихся в изотопе, равно произведению постоянной Авогадро N_А на количество вещества ν

Данного изотопа:

, (7)

где m- масса изотопа; М- молярная масса.

С учетом выражений (6) и (7) формулы (5) и (4) принимают вид

(8),

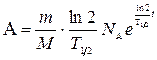(9).

Произведем вычисления, учитывая, что Т_1/2=600с (см табл. 13 Приложения), ln2=0,693; t=6 ч = 2,16·10⁴с:

 

Задачи для контрольных работ.

1. Точка движется по окружности радиусом R=1,2 м. Уравнение движения точки где А=0,5 рад/с; В=0,2 рад/с³. Определить тангенциальное а_τ, нормальное а_n и полное а ускорения точки в момент времени t =4 с.

2. Определить скорость υ и полное ускорение а точки в момент времени t =2 с, если она движется по окружности радиусом R =1 м согласно уравнению ξ=At+Bt³, где А=8 м/с; В=-1 м/с³; ξ – криволинейная координата, отсчитанная от некоторой точки, принятой за начальную, вдоль окружности.

3. По прямой линии движутся две материальные точки согласно уравнениями: и , где А ₁=10 м; В ₁=1 м/с; С ₁=-2 м/с²; А ₂=3 м; В ₂=2 м/с; С ₂=0,2 м/с². В какой момент времени τ скорости этих точек будут одинаковы? Найти ускорение а ₁ и а ₂ этих точек в момент t =3 с.

4. Определить полное ускорение а в момент t =3 с точки, находящейся на ободе колеса радиусом R =0,5 м, вращающегося согласно уравнению где А =2 рад/с; В =0,2 рад/с³.

5. Точка движется по окружности радиусом R =8 м. В некоторой момент времени нормальное ускорение точки а_n= 4 м/с², вектор полного ускорения а образует в этот момент с вектором нормального ускорения а_n угол α=60⁰. Найти скорость υ и тангенциальное ускорение а_τ точки.

6. Точка движется по прямой согласно уравнению где А =6 м/с; В = –0,125 м/с³. Определить среднюю путевую скорость <υ> точки в интервале времени от t₁ =2 с до t₂=6 с.

7. Материальная точка движется прямолинейно. Уравнение движения имеет вид х=Аt+Вt³, где А =3 м/с; В =0,06 м/с³. Найти скорость υ и ускорение а точки в моменты времени t=0 и t₂=3 с. Каковы средние значения скорости <υ_x> и ускорения < а _x> за первые 3 с движения?

8. Диск радиусом R =0,2 м вращается согласно уравнению φ=А+Вt+Сt³, где А =3 рад; В = – 1 рад/с; С =0,1 рад/с³. Определить тангенциальное а_τ, нормальное а_n и полное а ускорения точек на окружности диска для момента времени t = 10с.

9. С высоты h =2 м на стальную плиту свободно падает шарик массой т =200 г и подпрыгивает на высоту h ₁=0,5 м. Определить импульс р, полученный шариком при ударе.

10. При горизонтальном полете со скоростью υ =250.м/с снаряд массой т =8 кг разорвался на две части, Большая часть массой т ₁=6 кг получила скорость u ₁=400 м/с в направлении полета снаряда. Определить модуль и направление скорости u ₂ меньшей части снаряда.

11. Орудие, жестко закрепленное на железнодорожной платформе, производит выстрел вдоль полотна железной дороги под углом α=30⁰ к линии горизонта. Определить скорость u₂ отката платформы, если снаряд вылетает со скоростью u ₁=480 м/с. Масса платформы с орудием и снарядами т₂ =18 т, масса снаряда т₁= 60 кг.

12. Определить импульс р, полученный стенкой при ударе о нее шарика массой т =300 г, если шарик двигался со скоростью υ=8 м/с под углом α=60⁰ к плоскости стенки. Удар о стенку считать упругим.

13. Снаряд, летевший со скоростью υ=400 м/с, разорвался на два осколка. Меньший осколок, масса которого составляет 40 % от массы снаряда, полетел в противоположном направлении со скоростью и₁ = 150 м/с. Определить скорость и₂ большего осколка.

14. По небольшому куску мягкого железа, лежащему на наковальне массой т ₁=300 кг, ударяет молот массой т ₂=8 кг. Определить к. п. д. η удара, если удар неупругий. Полезной считать энергию, затраченную на деформацию куска железа.

15. Шар массой т ₁=1 кг движется со скоростью υ₁=4 м/с и сталкивается с шаром массой т ₂=2 кг, движущимся навстречу ему со скоростью υ₂=3 м/с. Каковы скорости и ₁ и и ₂ шаров после удара? Удар считать абсолютно упругим, прямым, центральным.

16. Шар массой т₁ =3 кг движется со скоростью υ₁=2 м/с и сталкивается с покоящимся шаром массой т ₂=5 кг. Какая работа будет совершена при деформации шаров? Удар считать абсолютно неупругим, прямым, центральным.

17. Определить к. п. д. η неупругого удара бойка массой т ₁=0,5 т, падающего на сваю массой т ₂=120 кг. Полезной считать энергию, затраченную на вбивание сваи.

18. Шар массой т₁ =4 кг движется со скоростью υ₁=5 м/с и сталкивается с шаром массой т ₂=6 кг, который движется ему навстречу со скоростью υ₂=2 м/с. Определить скорости и ₁ и и ₂ шаров после удара. Удар считать абсолютно упругим, прямым, центральным.

19. На покоящийся шар массой т₁ =5 кг налетает со скоростью υ₂=5 м/с шар массой т ₂=3 кг. Направление движения второго шара изменилось на угол α=45⁰. Определить скорости и ₁ и и ₂ шаров после удара, считая шары абсолютно упругими.

20. Атом распадается на две части массами кг и кг. Определить кинетические энергии Т₁ и Т₂ частей атома, если их общая кинетическая энергия Т =2,2∙10^-11 Дж. Кинетической энергией и импульсом атома до распада пренебречь.

21. Определить работу растяжения двух соединенных последовательно пружин жестокостями k ₁=400 Н/м и k ₂=250 Н/м, если первая пружина при этом растянулась на ∆ l =2 см.

22. Из ствола автоматического пистолета вылетела пуля массой т ₁=10 г со скоростью υ=300 м/с. Затвор пистолета массой т ₂=200 г прижимается к стволу пружиной, жесткость которой k =25 кН/м. На какое расстояние отойдет затвор после выстрела? Считать, что пистолет жестко закреплен.

23. Пружина жесткостью k =500 Н/м сжата силой F =100 Н. Определить работу А внешней силы, дополнительно сжимающей эту пружину еще на ∆ l =2 см.

24. Две пружины жесткостью k ₁=0,5 кН/м и k ₂=1 кН/м скреплены параллельно. Определить потенциальную энергию П данной системы при абсолютной деформации ∆ l =4 см.

25. Какую нужно совершить работу А, чтобы пружину жесткостью k =800 Н/м, сжатую на х =6 см, дополнительно сжать на ∆ х =8 см?

26. Если на верхний конец вертикально расположенной спиральной пружины положить груз, то пружина сожмется на ∆ l =3 мм. На сколько сожмет пружину тот же груз, упавший на конец пружины с высоты h =8 см?

27. Из пружинного пистолета с пружиной жесткостью k =150 Н/м был произведен выстрел пулей массой т =8 г. Определить скорость о пули при вылете ее из пистолета, если пружина была сжата на ∆ х =4 см.

28. Налетев на пружинный буфер, вагон массой т =16 т, двигавшийся со скоростью υ=0,6 м/с, остановился, сжав пружину на ∆ l =8 см. Найти общую жесткость k пружин буфера.

29. Цилиндр, расположенный горизонтально, может вращаться вокруг оси, совпадающей с осью цилиндра. Масса цилиндра т ₁=12 кг. На цилиндр намотали шнур, к которому привязали гирю массой т ₂=1 кг. С каким ускорением будет опускаться гиря? Какова сила натяжения шнура во время движения гири?

30. Через блок, выполненный в виде колеса, перекинута нить, к концам которых привязаны грузы массами т ₁=100 г и т ₂=300 г. Массу колеса М =200 г считать равномерно распределенной по ободу, массой спиц пренебречь. Определить ускорение, с которым будут двигаться грузы, и силы натяжения нити по обе стороны блока?

31. Определить скорость поступательного движения сплошного цилиндра, скатившегося с наклонной плоскости высотой h =20 см.

32. Тонкостенный цилиндр, масса которого т =12 кг, а диаметр основания D=30 см, вращается согласно уравнению , где А =4 рад; В =-2 рад/с; С =0,2 рад/с³. Определить действующий на цилиндр момент сил М в момент времени t =3 с.

33. На обод маховика диаметром D=60 см намотан шнур, к концу которого привязан груз массой т =2 кг. Определить момент инерции J маховика, если он, вращаясь равноускоренно под действием силы тяжести груза, за время t =3 с приобрел угловую скорость ω =9 рад/с.

34. Нить с привязанными к ее концам грузами массой т ₁=50 г и т ₂=60 г перекинута через блок диаметром D=4 см. Определить момент инерции J блока, если под действием силы тяжести грузов он получил угловое ускорение ε=1,5 рад/с².

35. Стержень вращается вокруг оси, проходящей через его середину согласно уравнению φ=Аt+Вt³, где А =2 рад/с; В =0,2 рад/с³. Определить вращающий момент М, действующий на стержень через t =2 с после начала вращения, если момент инерции стержня J =0,048 кгּ м².

36. По горизонтальной плоской поверхности катится диск со скоростью υ=8 м/с. Определить коэффициент сопротивления, если диск, будучи предоставленным самому себе, остановился, пройдя путь s =18 м.

37. Определить момент силы М, который необходимо приложить к блоку, вращающемуся с частотой п =12 с^-1, чтобы он остановился в течение времени ∆ t =8 с. Диаметр блока D=30 см. Массу блока т =6 кг считать равномерно распределенной по ободу.

38. Блок, имеющий форму диска массой т =0,4 кг, вращается под действием силы натяжения нити, к концам которой подвешены грузы массами т ₁=0,3 кг и т ₂=0,7 кг. Определить силы Т₁ и Т ₂ натяжения нити по обе стороны блока.

39. Шарик массой т =60 г, привязанный к концу нити длиной 1 ₁ =1,2 м, вращается с частотой п₁ =2 с^-1, опираясь на горизонтальную плоскость. Нить укорачивается, приближая шарик к оси вращения до расстояния 1 ₂=0,6 м. С какой частотой п ₂ будет при этом вращаться шарик? Какую работу А совершает внешняя сила, укорачивая нить? Трением шарика о плоскость пренебречь.

40. По касательной к шкиву маховика в виде диска диаметром D=75 см и массой т =40 кг приложен сила F =1 кН. Определить угловое ускорение ε и частоту вращения п маховика через время t =10 с после начала действия силы, если радиус r шкива равен 12 см. Силой трения пренебречь.

41. Определить возвращающую силу F в момент времени t =0,2 с и полную энергию Е точки массой т =20 г, совершающей гармонические колебания согласно уравнению х=Аsin ωt, где A =15 см; ω =4π c^-1.

42. Определить период Т колебаний стержня длиной 1 =30 см около горизонтальной оси, перпендикулярной стержню и проходящей через его конец.

43. Определить максимальное ускорение а_max материальной точки, совершающей гармонические колебания с амплитудой А =15 см, если наибольшая скорость точки υ=30 см/с. Написать также уравнение колебаний.

44. Точка совершает гармонические колебания, уравнение которых

х=Аsin ωt, где А =5 см; ω =2 c^-1. В момент времени, когда точка обладала потенциальной энергией П =0,1 мДж, на нее действовала возвращающая сила F =+5 мН. Найти этот момент времени t и соответствующую ему фазу φ колебаний.

45. Определить частоту ν гармонических колебаний диска радиусом R =20 см около горизонтальной оси, проходящей через середину радиуса диска перпендикулярно его плоскости.

46. Определить период Т гармонических колебаний диска радиусом R =40 см около горизонтальной оси, проходящей через образующую диска.

47. На стержне длиной 1 =30 см укреплены два одинаковых грузика: один – в середине стержня, другой – на одном из его концов. Стержень с грузиками колеблется около горизонтальной оси, проходящей через свободный конец стержня. Определить приведенную длину L и период Т гармонических колебаний. Массой стержня пренебречь.

48. Найти максимальную кинетическую энергию Т _max материальной точки массой т =2 г, совершающей гармонические колебания с амплитудой А = 4 см и частотой ν=5 Гц;

49. Точка совершает гармонические колебания. В некоторый момент времени смещение точки х =5 см, скорость ее υ=20 см/с и ускорение а =-80 см/с². Найти циклическую частоту и период колебаний, фазу колебаний в рассматриваемый момент времени и амплитуду колебаний.

50.Точка совершает гармонические колебания, уравнение которой имеет вид , где А=5 см; ω=2 с^-1. Найти момент времени (ближайший к началу отсчета), в который потенциальная энергия точки П =10^-4 Дж, а возвращающая сила F =+5·10^-3 Н. Определить также фазу колебаний в этот момент времени.

51. Баллон объемом V=20 л заполнен азотом при температуре T=400 К. Когда часть газа израсходовали, давление в баллоне понизилось на Δ р=200 кПа. Определить массу т израсходованного азота. Процесс считать изотермическим.

52. В баллоне объемом V= 15 л находится аргон под давлением р₁=600 кПа и температуре Т₁=300 К. Когда из баллона было взято некоторое количество газа, давление в баллоне понизилось до р₂=400 кПа, а температура установилась Т₂=260 К. Определить массу т аргона, взятого из баллона,

53. Количество вещества ν кислорода равно 0,5 моль. Определить внутреннюю энергию U водорода, а также среднюю кинетическую энергию молекулы этого газа при температуре Т=З00 К.

54. Один баллон объемом V₁=10 л содержит кислород под давлением р₁= 1,5 МПа, другой баллон объемом V₂=22 л содержит азот под давлением р₂=0,6 МПа. Когда баллоны соединили между собой, оба газа смешались, образовав однородную смесь (без изменения температуры). Найти парциальные давления р₁ и р₂ обоих газов в смеси и полное давление р смеси.

55. Смесь водорода и азота общей массой т =290 г при температуре Т=600 К и давлении р=2,46 МПа занимает объем V=30 л. Определить массу т ₁ водорода и массу т ₂ азота.

56. В баллоне объемом V=22,4 л находится водород при нормальных условиях. После того как в баллон было дополнительно введено некоторое количество гелия, давление в баллоне возросло до р=0,25 МПа, а температура не изменилась. Определить массу т гелия, введенного в баллон.

57. Водород находится при температуре Т=300 К. Найти среднюю кинетическую энергию вращательного движения одной молекулы, а также суммарную кинетическую энергию Е_к, всех молекул этого газа; количество вещества водорода ν=0,5 моль.

58. В азоте взвешены мельчайшие пылинки, которые движутся так, как если бы они были очень крупными молекулами. Масса т каждой пылинки равна 6∙ 10^-10 г. Газ находится при температуре Т=400 К. Определить средние квадратичные скорости (υ_кв), а также средние кинетические энергии <ε_пост > поступательного движения молекулы азота и пылинки.

59. Определить показатель адиабаты у идеального газа, который при температуре Т= 350 К и давлении р= 0,4 МПа занимает объем V=300 л и имеет теплоемкость С _v =857 Дж/К.

60. В сосуде объемом V=6 л находится при нормальных условиях двухатомный газ. Определить теплоемкость С _v этого газа при постоянном объеме.

61. Найти среднее число (z) столкновений за время t=1 с и длину свободного пробега (1) молекулы гелия, если газ находится под давлением р =2 кПа при температуре Т =200 К.

62. Найти среднюю длину свободного пробега (1) молекулы азота в сосуде объемом V=5 л. Масса газа т =0,5 г.

63. Водород находится под давлением р =20 мкПа и имеет температуру Т =300 К. Определять среднюю длину свободного пробега (1) молекулы такого газа.

64. При нормальных условиях длина свободного пробега <1> молекулы водорода равна 0,160 мкм. Определить диаметр d молекулы водорода.

65. Какова средняя арифметическая скорость (υ) молекул кислорода при нормальных условиях, если известно, что средняя длина свободного пробега (1) молекулы кислорода при этих условиях равна 100 нм.

66. Кислород находится под давлением р=133 нПа при температуре Т =200 К. Вычислить среднее число <z> столкновений молекулы кислорода при этих условиях за время t=1 с.

67. Водород массой т =2 г занимает объем V =2,5 л. Определить среднее число (z) столкновений молекулы водорода за время τ=1 с.

68. Средняя длина свободного пробега (1) молекулы водорода при некоторых условиях равна 2 мм. Найти плотность q водорода при этих условиях.

69. При адиабатном сжатии давление воздуха было увеличено от р₁=50 кПа до р₂=0,5 МПа. Затем при неизменном объеме температура воздуха была понижена до первоначальной. Определить давление р₃ газа в конце процесса.

70. Кислород массой т =200 г занимает объем V ₁=100 л и находится.под давлением р₁=200 кПа. При нагревании газ расширился при постоянном давлении до объема V ₂=300 л, а затем его давление возросло до р₂=500 кПа при неизменном объеме. Найти изменение внутренней энергии ∆U газа, совершенную им работу А и теплоту Q, переданную газу. Построить график процесса.

71. Объем водорода при изотермическом расширении (Т=300 К) увеличился в п =3 раза. Определить работу А, совершенную газом, и теплоту Q, полученную им при этом. Масса т водорода равна 200 г.

72. Водород массой т =40 г, имевший температуру Т=300 К, адиабатно расширился, увеличив объем в п ₁=3 раза. Затем при изотермическом сжатии объем газа уменьшился в п₂ =2 раза. Определить полную работу А, совершенную газом, и конечную температуру Т газа.

73. Азот массой т =0,1 кг был изобарно нагрет от температуры Т₁ =200 К до температуры Т ₂=400 К. Определить работу А, совершенную газом, полученную им теплоту Q и изменение ∆U внутренней энергии азота.

74. Кислород массой т =250 г, имевший температуру Т ₁=200 К, был адиабатно сжат. При этом была совершена работа А =25 кДж. Определить конечную температуру Т газа.

75. Во сколько раз увеличится объем водорода, содержащий количество вещества ν=0,4 моль при изотермическом расширении, если при этом газ получит теплоту Q=800 Дж? Температура водорода Т= 300 К.

76. В баллоне при температуре Т ₁=145 К и давлении р₁=2 МПа находится кислород. Определить температуру Т₂ и давление р₂ кислорода после того, как из баллона будет очень быстро выпущена половина газа.

77. Определить работу А₂ изотермического сжатия газа, совершающего цикл Карно, к. п. д. которого η=0,4, если работа изотермического расширения равна А₁=8 Дж.

78. Газ, совершающий цикл Карно, отдал теплоприемнику теплоту Q₂=14 кДж. Определить температуру Т₁ теплоотдатчика, если при температуре теплоприемника Т₂=280 К работа цикла А=6 кДж.

79. Газ, являясь рабочим веществом в цикле Карно, получил от теплоотдатчика теплоту Q₁=4,38 кДж и совершил работу А=2,4 кДж. Определить температуру теплоотдатчика, если температура теплоприемника Т₂=273 К.

80. Газ, совершающий цикл Карно, получает теплоту Q₁=84 кДж. Определить работу 4 газа, если температура Т₁ теплоотдатчика в три раза выше температуры Т₂ теплоприемника.

81. Точечные заряды Q = 20 мкКл, Q=-10 мкКл находятся на расстоянии d = 5 см друг от друга. Опреде­лить напряженность поля в точке, удаленной на r₁=3 см от первого и на г₂ = 4 см от второго заряда. Определить также силу F, действующую в этой точке на точечный заряд Q= 1 мкК.

82. Три одинаковых точечных заряда Q₁ = Q₂ = Q₃ = 2 нКл находятся в вершинах равностороннего тре­угольника со сторонами а=10см. Определить модуль и направление силы F, действующей на один из зарядов со стороны двух других.

83. Четыре одинаковых заряда Q₁ = Q₂ = Q₃ = Q₄=40 нКл закреплены в вершинах квадрата со стороной а=10 см. Найти силу F, действующую на один из этих зарядов со стороны трех остальных.

84. Точечные заряды Q₁=30 мкКл и Q₂= - 20 мкКл находятся на расстоянии d = 20 см друг от друга. Опре­делить напряженность электрического поля Е в точке, удаленной от первого заряда на расстояние r₁ = 30 см, а от второго — на г₂= 15 см.

85. В вершинах правильного треугольника со сторо­ной, а = 10 см находятся заряды Q₁ = 10 мкКл, Q₂ = 20 мкКл и Q₃ = 30 мкКл. Определить силу F, действую­щую на заряд Q₁ со стороны двух других зарядов.

86. На расстоянии d= 20 см находятся два точечных заряда Q₁ = — 50 нКл и Q₂=100 нКл. Определить си­и F, действующую на заряд Q₃= -10 нКл, удаленный от обоих зарядов на одинаковое расстояние, равное d.

87. Два точечных заряда Q₁ = 6 нКл и Q₂ = 3 нКл находятся на расстоянии d=60 см друг от друга. Какую работу необходимо совершить внешним силам, чтобы уменьшить расстояние между зарядами вдвое?

88. Пылинка массой m = 200 мкг, несущая на себе заряд Q = 40 нКл, влетела в электрическое поле в на­правлении силовых линий. После прохождения разности потенциалов U = 200 В пылинка имела скорость v = 10 м/с. Определить скорость v пылинки до того, как она влетела в поле.

89. Электрон, обладавший кинетической энергией Т = 10 Эв, влетел в однородное электрическое поле в направлении силовых линий поля. Какой скоростью будет обладать электрон, пройдя в этом поле разность потен­циалов U= 8 в?

90. Пылинка массой т = 5 нг, несущая на себе N = 10 электронов, прошла в вакууме ускоряющую раз­ность потенциалов U= 1 МВ. Какова кинетическая энер­гия Т пылинки? Какую скорость v приобрела пылинка?

91. Конденсаторы емкостью С₁ = 5 мкФ и С₂ = = 10 мкФ заряжены до напряжений U₁= 60 В и U₂ = = 100 В соответственно. Определить напряжение на обкладках конденсаторов после их соединения обкладками, имеющими одноименные заряды.

92. Конденсатор емкостью C₁= 10 мкФ заряжен до напряжения U = 10 В. Определить заряд на обкладках этого конденсатора после того, как параллельно ему был подключен другой, незаряженный, конденсатор ем­костью C₁ = 20 мкФ.

93. Конденсаторы емкостями C₁ = 2мкФ, C₂ = = 5 мкФ и Сз = 10 мкФ соединены последовательно и находятся под напряжением U = 850 В. Определить на­пряжение и заряд на каждом из конденсаторов.

94. Два конденсатора емкостями С₁ = 2 мкФ и С₂= = 5 мкФ заряжены до напряжений U₁ = 100 В и U₂ = 150 В соответственно. Определить напряжение на об­кладках конденсаторов после их соединения обкладками, имеющими разноименные заряды.

95. Два одинаковых плоских воздушных конденсато­и емкостью С=100 Пф каждый соединены в батарею последовательно. Определить, на сколько изменится емкость С батареи, если пространство между пластинами одного из конденсаторов заполнить парафином.

96. Два конденсатора емкостями С₁= 5 мкФ и С₂ = 8 мкФ соединены последовательно и присоединены к батарее с ЭДС E =80 В. Определить заряды Q₁ и Q₂ конденсаторов и разности потенциалов U₁и U₂между их обкладками.

97. Плоский конденсатор состоит из двух круглых пластин радиусом R = 10 см каждая. Расстояние между пластинами d= 2 мм. Конденсатор присоединен к источ­ика напряжения U= 80 В. Определить заряд Q и на­пряженность Е поля конденсатора в двух случаях: а) диэлектрик — воздух; б) диэлектрик — стекло.

98. Два металлических шарика радиусами R₁ = 5 см и R₂ = 10 см имеют заряды Q₁ = 40 нКл и Q₂ =-20 нКл соответственно. Найти энергию W, которая выделится при разряде, если шары соединить проводни­ком.

99. Пространство между пластинами плоского кон­денсатора заполнено двумя слоями диэлектрика: стекла толщиной d₁= 0,2 см и слоем парафина толщиной d₂ = 0,3 см. Разность потенциалов между обкладками U =300 В. Определить напряженность Е поля и падение потенциала в каждом из слоев.

100. Плоский конденсатор с площадью пластин S = 200 см² каждая заряжен до разности потенциалов U = 2 Кв. Расстояние между пластинами d = 1см. Диэлект­рик — стекло. Определить энергию W поля конденсатора и плотность энергии w поля.

101. Катушка и амперметр соединены последователь­но и подключены к источнику тока. К клеммам катушки присоединен вольтметр с сопротивлением г = 4 кОм. Ам­перметр показывает силу тока I = 0,3 А, вольтметр — напряжение U = 120 В. Определить сопротивление Rкатушки.

102. ЭДС батареи ε = 80 В, внутреннее сопротивле­ние R_i = 5 Ом. Внешняя цепь потребляет мощность Р = 100 Вт. Определить силу тока I в цепи, напряжение U, под которым находится внешняя цепь, и ее сопротивление R.

103. От батареи, ЭДС которой 600 В, требуется передать энергию на расстояние L = 1 км. Потребляемая мощность Р = 5 кВт. Найти минимальные потери мощ­ности в сети, если диаметр медных подводящих проводов d = 0,5 см.

104. При внешнем сопротивлении R₁ = 8 Ом сила тока в цепи I₁ = 0,8 А, при сопротивлении R₂ = 15 Ом сила тока I₂ = 0,5 А, Определить силу тока I_к.₃ короткого замыкания источника ЭДС.

105. ЭДС батареи ε = 24 В. Наибольшая сила тока, которую может дать батарея, I_max= 10 А. Определить максимальную мощность Р_mах, которая может выделяться во внешней цепи.

106. Аккумулятор с ЭДС ε= 12 В заряжается от сети постоянного тока с напряжением U=15 В. Определить напряжение на клеммах аккумулятора, если его внутрен­нее сопротивление R_i= 10 Ом.

107. От источника с напряжением U= 800 В необхо­димо передать потребителю мощность Р= 10 кВт на не­которое расстояние. Какое наибольшее сопротивление может иметь линия передачи, чтобы потери энергии в ней не превышали 10% от передаваемой мощности?

108. При включении электромотора в сеть с напряже­нием U = 220 В он потребляет ток I = 5 А. Определить мощность, потребляемую мотором, и его КПД, если сопротивление R обмотки мотора равно 6 Ом.

109. В сеть с напряжением U = 100 В подключили катушку с сопротивлением R₁ = 2 кОм и вольтметр, сое­диненные последовательно. Показание вольтметра U₁ = 80 В. Когда катушку заменили другой, вольтметр по­казал U₂ = 60 В. Определить сопротивление R₂ другой катушки.

110. ЭДС батареи ε=12 В. При силе тока I = 4 А КПД баратери η= 0,6. Определить внутреннее сопротив­ление R_i батареи.

111. За время t=20 с при равномерно возраставшей силе тока от нуля до некоторого максимума в проводнике сопротивлением R = 5 Ом выделилось количество тепло­ты Q = 4 кДж. Определить скорость нарастания силы тока.

112. Сила тока в проводнике изменяется со временем по закону I = I₀e^-αt, где I₀ = 20 А, а α = 10²с^-1. Опреде­лить количество теплоты, выделившееся в проводнике за время t = 10^-2 с.

113. Сила тока в проводнике сопротивлением R = 10 Ом за время t = 50 с равномерно нарастает от I₁ = 5 А до I₂ = 10 А. Определить количество теплоты Q, выделившееся за это время в проводнике.

114. В проводнике за время t= 10 с при равномерном возрастании силы тока от I₁ = 1 А до I₂ = 2 А выдели­лось количество теплоты Q = 5 кДж. Найти сопротив­ление Rпроводника.

115. Сила тока в проводнике изменяется со временем по закону I = I_оsinωt Найти заряд Q, проходящий через поперечное сечение проводника за время t, равное поло­вине периода T, если начальная сила тока I₀ = 10 А, цик­лическая частота ω = 50πс^-1.

116. За время t = 10 с при равномерно возрастающей силе тока от нуля до некоторого максимума в проводнике выделилось количество теплоты Q = 40 кДж. Определить среднюю силу тока <I> в проводнике, если его сопро­тивление R = 25 Ом.

117. За время t=8 с при равномерно возраставшей силе тока в проводнике сопротивлением R = 8 Ом выде­лилось количество теплоты Q = 500 Дж. Определить за­ряд q, проходящий в проводнике, если сила тока в на­чальный момент времени равна нулю.

<