Домашнее задание №№884(б,е,к,г,з,м),№885,№887

Разложение разности квадратов на множители.

Цель урока: повторить изученные ранее формулы сокращенного умножения, формировать навыки применение этих формул при преобразовании выражений, ввести метод разложения разности квадратов на множители, отрабатывать навыки его применения, развивать умение выбора того или иного метода преобразования выражения по его виду.

План урока

1. Организационный момент.

2. Устная работа

3. Проверочная работа

4. Актуализация знаний

5. Формирование навыков

6. Итог урока. Домашнее задание

Ход урока

1. Организационный момент. Приветствие учителя. Подготовка к работе.

Устная работа

Для работы на уроке нам необходимо повторить как представить выражение в виде квадрата одночлена:

а)81

Выполнить умножение

a) (a-2)(a+2); б) (-x²-4)(4-x²); в)(y+5)(5-y); г)(3a³-x)(x+3a³)

Проверочная работа

4. Актуализация знаний. Выпишем на доске все формулы сокращенного умножения, которые мы изучили на предыдущих уроках:

1. Квадрат суммы (a + b)² = a² + 2ab +b²

2. Квадрат разности (a – b)² = a² – 2ab + b²

3. Куб суммы (a +b)³= a³ + 3a²b + 3ab² +b³

4. Куб разности (a -b)³= a³ -3a²b + 3ab² -b³

5. Разность квадратов (a-b)(a +b)=a² –b²

Хорошо, давайте рассмотрим выражение x² + 14x + 49, как можно преобразовать данное выражение? Ребята отвечают, что нам дана часть формулы квадрата суммы и можно разложить это выражение на множители, воспользовавшись продолжением этой формулы, а именно

x² + 14x + 49 = (x + 7)²

ребята, скажите, а что если поменять местами правую и левую части последней формулы – формулы разности квадратов?

Учащиеся ответят, что разницы нет как записать равенство, будет та же самая формула.

a² –b²= (a-b)(a +b)

а как будет называться данное преобразование выражения? Что мы видим в правой части? Произведение двух скобок, т.е……(учитель подталкивает учащихся к понятию того, что таким образом мы раскладываем на множители разность квадратов) Ребята должны сами проговорить, что это именно разложение на множители.

Ребята как вы думаете какова тема нашего сегодняшнего урока? Учащиеся формулируют тему урока, при необходимости учитель корректирует формулировку. Чему мы должны научиться на этом уроке? Определяются цели урока.

5. Формирование навыков.

Рассмотрим примеры у доски 36 – х² = (6)² – (х)² =(6 – х)(6 + х)

49х² – 16y² = (7х)² – (4y)² = (7х-4y)(7х + 4y)

Перейти к решению номеров из учебника (7 кл. алгебра Макарычев)

№883 (в,е,и,м) к доске вызываются два человека, остальные решают примеры в тетрадях сверяясь с доской, учитель проходит по рядам, оказывая индивидуальную ребятам помощь в решении.

№884 (а,д,и, в,ж,л) на работу с данными выражениями можно вызвать менее подготовленных учащихся.

№886(б,г,е)

Б) 53² – 63² = (53- 63) (53+63) =- 10 * 116= - 1160

Г) 21,3² – 21,2² = (21,3 – 21,2) (21,3 +21,2)=0,1 *42,5 = 4,25

Е)

№889 (д,е)

Решение предыдущего номера поможет в решении следующих примеров, входе их решения учащиеся должны четко уяснить, что решение по формуле, значительно облегчает вычисления значений данных выражений.

№889 (а,б,г,д)

6. Подведение итогов. Какой способ разложения на множители мы изучили?

Все ли выражения можно разложить этим способом?

Домашнее задание №№884(б,е,к,г,з,м),№885,№887

Далее ребятам предлагается каждому «Билет на выход»

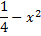
Если возможно разложить на множители	Если возможно разложить на множители
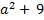
Если возможно разложить на множители	Если возможно разложить на множители

Данные билеты ребята подписывают и сдают учителю, причем каждый билет проверяется учителем сразу, если в нем есть ошибки ученик должен эти ошибки исправить (учитель может подсказать где содержится ошибка, но исправить ее должен сам учащийся).