Уравнения электрического поля
Теорема Гаусса
Поток вектора напряженности электростатического поля в вакууме через произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на
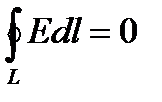Циркуляция вектора напряженности электростатического поля равна 0
Теорема Остроградского-Гаусса:
Поток вектора электрического смещения в вакууме через произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов
Напряженность поля – сила, действующая на единичный положительный пробный заряд (q), внесенный в электростатическое поле заряда Q:
Закон Кулона:
Уравнение Лапласа для электрического поля в проводящей среде: Как в электростатическом поле, так и в поле постоянного тока (в области где нет сторонних э.д.с.), напряженность E:
Закон электромагнитной индукции в дифференциальной форме
(это есть 1-ое уравнение теории Максвелла)
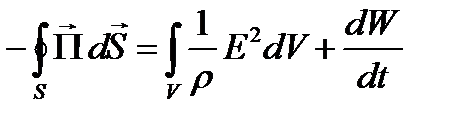Теорема Умова-Пойнтинга: Поток вектора Пойнтинга, входящий в замкнутую поверхность S, равен сумме двух мощностей:
Законы электрических цепей
1ый закон Кирхгофа: Алгебраическая сумма токов ветвей, сходящихся в узле электрической цепи, равна нулю: 
.
2ой закон Кирхгофа: Алгебраическая сумма напряжений ветвей в контуре равна сумме ЭДС действующих в контуре: 
.
Закон Ома в комплексной форме: 
называют комплексным сопротивлением участка цепи.
Представим комплексное сопротивление в показательной форме:
.
Модуль комплексного сопротивления равен отношению амплитуд (действующих значений) напряжения и тока:
.Его называют полным сопротивлением.
Дифференциальная форма закона Джоуля-Ленца:
Мощность тепловых потерь в проводнике:
Цепи синусоидального тока
Производство, передача и распределение электрической энергии осуществляются преимущественно на синусоидальном переменном токе. Это объясняется тем, что для передачи и распределения электрической энергии требуются напряжения разного уровня.
Токи и напряжения, мгновенные значения которых повторяются через равные промежутки времени, называют периодическими. Наименьший промежуток времени, через который значения периодического тока повторяются, называют периодом.
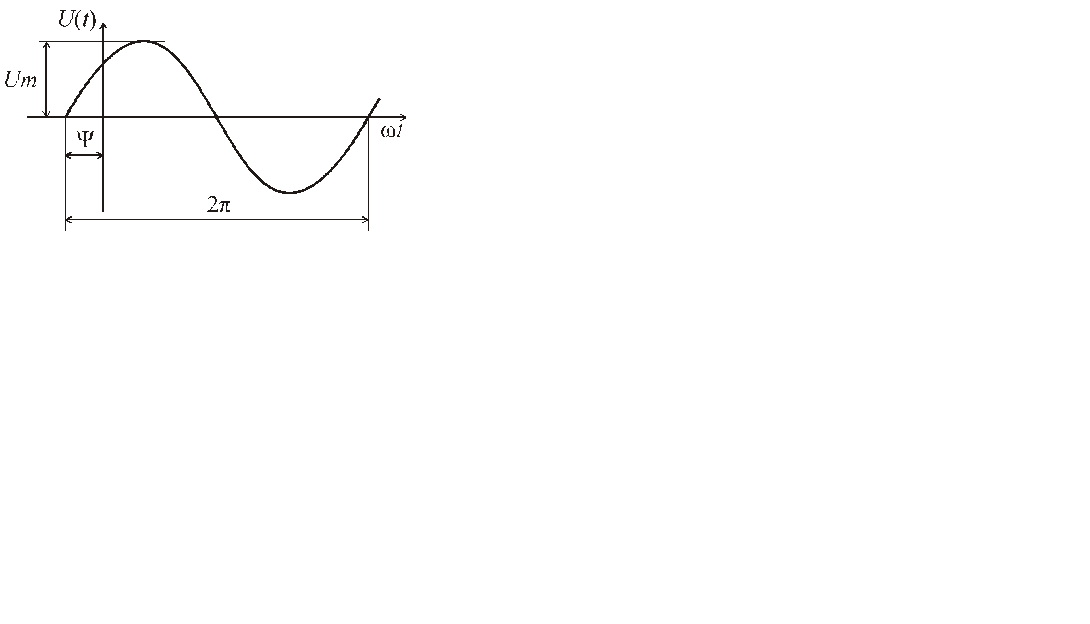
Величину, обратную периоду, называют циклической частотой: 
Простейшей периодической функцией является синусоидальная функция. Мгновенное значение синусоидальной функции времени определяется равенством 
.
О величине переменного тока судят по его среднему или действующему значению.
Среднее значение периодической функции времени 
определяют по формуле 
.
Среднее значение синусоидальной функции за период равно нулю. Поэтому используют понятие среднего значения за половину периода: 
.
Действующее значение переменного тока 
определяется по формуле 
.
действующее значение синусоидального тока равно такому постоянному току, при котором в резисторе за период выделяется такое же количество тепла, что и при переменном.
Среднее значение мгновенной мощности 
за период Т называют активной или средней мощностью: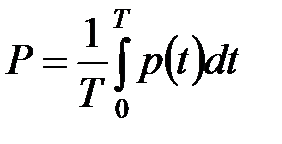 
.
активная мощность 
.
Индуктивный элемент
Предположим, что ток индуктивного элемента изменяется синусоидально. Для упрощения выкладок примем начальную фазу тока равной нулю: 
.
Напряжение индуктивного элемента 
Ток индуктивного элемента отстает по фазе от приложенного напряжения на угол 
или на четверть периода. Амплитуда напряжения индуктивного элемента 
.
Величину 
, имеющую размерность сопротивления, называют индуктивным сопротивлением. Индуктивное сопротивление является линейной функцией частоты w.
Временные диаграммы напряжения и тока индуктивного элемента показаны на рисунке
Мгновенная мощность индуктивного элемента
.
Учитывая, что действующие значения синусоидальных величин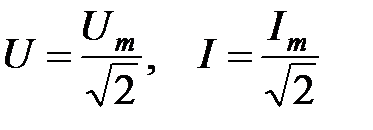 
, окончательно получим 
.
Энергия, запасаемая в магнитном поле индуктивного элемента в первую четверть периода, во вторую четверть периода возвращается во внешнюю цепь. Это соответствует определению идеального индуктивного элемента, в соответствии с которым в этом элементе происходит только запасание энергии магнитного поля, а потери энергии отсутствуют.
Емкостный элемент
Предположим, что напряжение емкостного элемента – синусоидальная функция времени 
.
Ток емкостного элемента 
.
Ток емкостного элемента опережает напряжение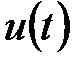 
на угол 
или на четверть периода. Амплитуда тока 
.
Величину 
, имеющую размерность проводимости, называют емкостной проводимостью. Величина, обратная емкостной проводимости, – емкостноесопротивление: 
.
Мгновенная мощность емкостного элемента 
.
Трехфазные цепи
Для получения и передачи электрической энергии используют трехфазные цепи. Трехфазной называют совокупность трех однофазных цепей (фаз), в каждой из которых действуют ЭДС одинаковой частоты, сдвинутые друг относительно друга на одинаковый угол, равный 120°, и создаваемые общим источником. В качестве источников используются трехфазные синхронные генераторы.
Передача энергии с помощью трехфазных цепей экономически более выгодна, чем с помощью однофазных цепей, Если нагрузка всех фаз трехфазного генератора одинакова, то мгновенная мощность постоянна.
Мгновенные значения ЭДС трехфазного генератора
, 
, 
.
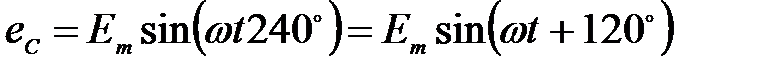Начальная фаза ЭДС 
, а начальная фаза ЭДС 
. Такую систему ЭДС называют симметричной. Фазные ЭДС в комплексной форме
, 
, 
. 
При соединении звездой концы всех фаз генератора соединяют в один узел. Его называют нейтральным узлом или нейтральной точкой.
При соединении звездой линейное напряжение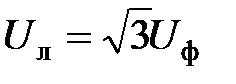 
. 
При соединении треугольником начало
одной фазной обмотки соединяют с
концом следующей так, чтобы три обмотки образовали замкнутый треугольник.
На практике используют различные комбинации соединения фаз генератора и нагрузки: звезда-звезда, звезда-треугольник, треугольник-треугольник и т. д.
Мгновенная мощность трехфазной цепи равна алгебраической сумме мгновенных мощностей отдельных фаз: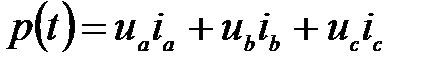 
.
Активная мощность трехфазной цепи при одинаковой нагрузке фаз равна мгновенной мощности 
, Где 
– угол сдвига фаз между фазными напряжениями и токами.
Реактивная мощность трехфазной цепи 
.
Если нагрузка фаз одинакова, достаточно измерить мощность, потребляемую одной фазой, и эту величину умножить на три:
.
При неодинаковых сопротивлениях фаз приемника, соединенных звездой с нейтральным проводом, необходимы три ваттметра, каждый из которых измеряет мощность одной фазы приемника.
В трехфазной системе без нейтрального провода мощность можно измерить с помощью двух ваттметров.
5.(5) Нелинейные электрические и магнитные цепи
Существуют так же элементы, параметры которых существенно зависят от напряжений и токов. Такие элементы называют нелинейными. Их свойства нельзя определить одним постоянным параметром. Для определения свойств нелинейных элементов необходимо задать зависимости, называемые характеристиками. Характеристики элементов снимают экспериментально и представляют графически или аналитически.
Пример1. Лампа накаливания.
ВАХ лампы накаливания
Если изменения идет от – u0 до +u0,то этот элемент линейный, мы можем определить сопротивление R, при большем диапазоне изменения напряжения этот элемент нелинейный.
Пример 2. Диод полупроводниковый.
ВАХ диода
Индуктивный элемент. Поведение нелинейного индуктивного элемента определяется зависимостью между потокосцеплением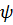 
и током I. Зависимость 
называют Вебер-амперной характеристикой. Для каждой точки Вебер-амперной характеристики можно определить статическую и динамическую индуктивность. Lст= 
в выбранной точке, а динамическая – это отношение малых Lд= 
.
Емкостный элемент. Поведение емкостного элемента определяется зависимостью между зарядом и напряжением Q=f(U). Эту зависимость называют кулон-вольтной характеристикой. Условно-графическое обозначение нелинейного емкостного элемента.
Сст= 
в выбранной точке КВХ; Сд= 
Основные особенности нелинейных цепей - неприменимость принципа наложения!
Явления, которые могут происходить только в нелинейных цепях:
Если на входе цепи действует источник синусоидального сигнала, то форма выходного сигнала будет отличаться отсинусоидальной, ее можно разложить на сумму гармоник кратных частот (в ряд Фурье).
В нелинейных цепях амплитуда выходная не пропорциональна амплитуде входного воздействия.
В некоторых нелинейных цепях при изменении амплитуды входного сигнала, выходной сигнал остается неизменным. Также цепи используют в качестве стабилитронов токов и напряжений.
В нелинейных цепях могут наблюдаться установившиеся незатухающие колебания. При этом источник внешнего периодического сигнала отсутствует. Такое явление называется автоколебаниями.
Магнитные цепи
Магнитной цепью называют совокупность устройств, по которым замыкается магнитный поток. Магнитные цепи, как правило, содержат катушки, сердечники из ферромагнитных материалов, обладающие высокой магнитной проницаемостью, участки из неферромагнитных материалов (воздушные зазоры).
Основными величинами, характеризующими магнитное поле, являются вектор магнитной индукции 
и вектор напряженности магнитного поля 
. Вектор напряженности магнитного поля связан с вектором магнитной индукции соотношением: B = 
H = 
H.
Здесь 
относительная магнитная проницаемость, 
магнитная постоянная, 
абсолютная магнитная проницаемость, измеряемая в Гн/м. Магнитная постоянная 
=4 
∙10-7 Гн/м.
В сердечниках из ферромагнитных материалов зависимость между В и Н имеет нелинейный характер. График зависимости магнитной индукции от напряженности магнитного поля В = f (H) называют кривой намагничивания.
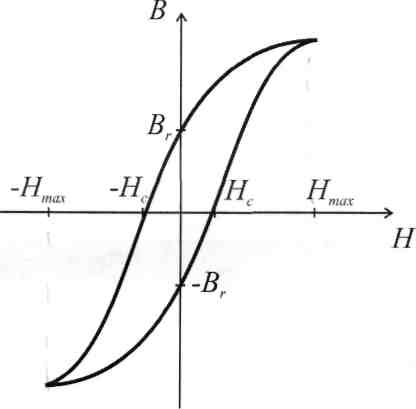В том случае, когда ток в обмотке катушки, намотанной на ферромагнитный сердечник, изменяется периодически, кривая зависимости В = f(H) приобретает вид петли гистерезиса. Размеры петли зависят в основном от материала сердечника, от наибольшего значения магнитной индукции, а также от скорости перемагничивания. Ферромагнитные материалы с широкой петлей гистерезиса (Нс >4000А/м) называют магнитно-твердыми. Материалы с узкой петлей гистерезиса (Нс <200А/м) называют магнитно-мягкими. Магнитно-твердые материалы используют в постоянных магнитах. Магнитно-мягкие материалы применяют в переменных магнитных полях.
Задача расчета магнитных цепей заключается в том, что по известным конфигурации, геометрическим размерам и материалам участков магнитопровода необходимо определить:1. Намагничивающие силы обмоток по заданному потоку;
2. Поток по заданным намагничивающим силам.