Дисциплина: ЕН.01 Математика: алгебра и начала математического анализа, геометрия
Группа: ТЭЭО -19
Дата: 20.10. 2020
Преподаватель: Кулага Т.Ф.
Задание: Ф ото выполненной работы прислать по адресу: kitdistergo@mail.ua kitdisttpop@mail.ua. или https://vk.com/id596417775 личным сообщением
(Название файла с ответами: № занятия, дисциплина, группа, Фамилия, имя, студента).
Например, Иванов И.И., ТЭЭО -19, Математика: алгебра и начала математического анализа, геометрия
Сроки выполнения: 21.10.2020
Задания для дистанционного обучения будут выдаваться в день проведения занятия, согласно расписанию и подмен по адресу: https://s3320.nubex.ru/5989/ или VK https://vk.com/ ТЭЭО-20-11, https://vk.com/ ТПОП-19
Мотивация
Три пути ведут к знанию:
Путь размышления – это путь самый благородный,
Путь подражания – это путь самый лёгкий и
Путь опыта - это путь самый горький….
Конфуций
Тема занятия: «ПОНЯТИЕ ПЕРВООБРАЗНОЙ И НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА»
ПЛАН
1. Понятие первообразной и неопределенного интеграла.
2. Свойства. Формулы интегрирования.
3. Решение примеров
Теоретические сведения
Первообразная
Функцию, восстанавливаемую по заданной ее производной или дифференциалу, называют первообразной.
Дифференцируемая функция 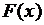 называется первообразной для функции
называется первообразной для функции 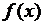 на заданном промежутке, если для всех х из этого промежутка справедливо равенство
на заданном промежутке, если для всех х из этого промежутка справедливо равенство 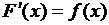 .
.

Из этого определения вытекает, что всякая функция по отношению к своей производной является первообразной.
Так, функция 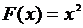 есть первообразная функции
есть первообразная функции 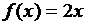 на интервале
на интервале  , поскольку для всех
, поскольку для всех 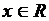 имеет место равенство
имеет место равенство 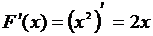 .
.
1. Найти первообразную функции  .
Решение: Используя правило дифференцирования, можно догадаться, что на интервале .
Решение: Используя правило дифференцирования, можно догадаться, что на интервале  первообразной является первообразной является 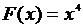 . Действительно, . Действительно, 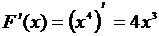 для всех для всех 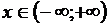 .
2. Найти первообразную функции .
2. Найти первообразную функции 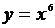 на множестве R.
Решение: Степень на множестве R.
Решение: Степень 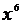 получается при дифференцировании получается при дифференцировании 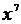 . Так как . Так как 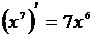 , то, чтобы при дифференцировании , то, чтобы при дифференцировании 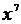 получить перед получить перед 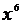 коэффициент 1, нужно коэффициент 1, нужно 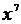 взять с коэффициентом 1/7. Следовательно, взять с коэффициентом 1/7. Следовательно, 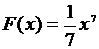 . .
|
Дифференцирование функции – однозначная операция, т.е. если функция имеет производную, то только одну. Это утверждение непосредственно следует из определений предела и производной: если функция имеет предел, то только один. Обратная операция – отыскание первообразной – не однозначна.
Так, функции 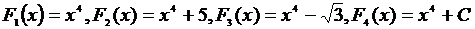 , где С – любое постоянное действительное число, являются первообразными функции
, где С – любое постоянное действительное число, являются первообразными функции  , поскольку все эти функции имеют одну и ту же производную
, поскольку все эти функции имеют одну и ту же производную 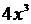 .
.
Теорема. Если 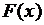 является первообразной функции
является первообразной функции 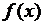 на некотором промежутке, то множество всех первообразных этой функции имеет вид
на некотором промежутке, то множество всех первообразных этой функции имеет вид 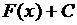 , где С – любое действительное число.
, где С – любое действительное число.
Неопределенный интеграл
Как уже было отмечено, первообразную можно находить не только по данной ее производной, но и по ее дифференциалу. В дальнейшее мы будем этим пользоваться.

Определение. Совокупность всех первообразных 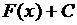 функции
функции 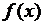 на рассматриваемом промежутке называется неопределенным интегралом и обозначается символом
на рассматриваемом промежутке называется неопределенным интегралом и обозначается символом 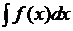 , где
, где 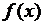 - подынтегральная функция,
- подынтегральная функция, 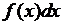 - подынтегральное выражение, х – переменная интегрирования.
- подынтегральное выражение, х – переменная интегрирования.
Таким образом, если 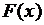 - какая-нибудь первообразная функции
- какая-нибудь первообразная функции 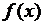 на некотором промежутке, то
на некотором промежутке, то 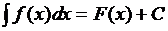 , где С – любое действительное число.
, где С – любое действительное число.
Замечание. Наличие постоянной С делает задачу нахождения функции по ее производной не вполне определенной; отсюда происходит название «Неопределенный интеграл».
Так, пользуясь определением неопределенного интеграла, можно записать: 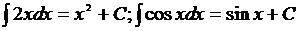 .
.
Значит, чтобы найти неопределенный интеграл от заданной функции, нужно найти какую-нибудь одну из ее первообразных и прибавить к ней произвольную постоянную С.
Слово «интеграл» происходит от латинского слова integer, что означает «восстановленный». Интегрируя какую-либо функцию, например 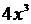 , мы как бы восстанавливаем функцию
, мы как бы восстанавливаем функцию 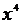 , производная которой равна
, производная которой равна 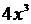 .
.
Чтобы проверить, правильно ли найден неопределенный интеграл, необходимо продифференцировать полученную функцию, если при этом получается подынтегральное выражение, то интеграл найден верно.
Например, 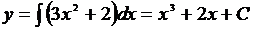 . Сделаем проверку:
. Сделаем проверку: 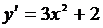 или
или 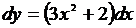 . Следовательно, интеграл найден верно.
. Следовательно, интеграл найден верно.
Основные свойства неопределенного интеграла
Из рассмотренных ранее примеров видно, что можно находить интегралы, подбирая первообразные. Однако это не всегда просто. При интегрировании помогает знание некоторых свойств интеграла, формул интегрирования, а также специальных приемов.
Рассмотрим сначала основные свойства неопределенного интеграла.




Формулы интегрирования
Из определения интеграла следует, что для того, чтобы проинтегрировать функцию, нужно найти ее первообразную. Для ряда функций это легко сделать, используя соответствующие формулу интегрирования.
Например, мы знаем, что 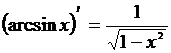 ; отсюда следует, что
; отсюда следует, что 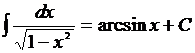 .
.
Итак, формулы интегрирования получаются обращением соответствующих формул дифференцирования. Выпишем в таблицу основные интегралы.


Вычисление интегралов способом приведения их к табличным с помощью преобразования подынтегрального выражения и применения свойств 2 и 3 неопределенного интеграла называется непосредственным интегрированием. При этом полезно запомнить, что 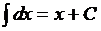 (формула 1 при
(формула 1 при  ).
).

2. 

3. 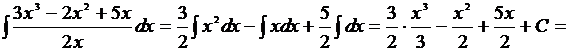
= 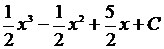
4. 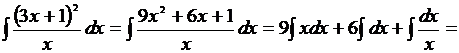
= 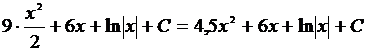
5. 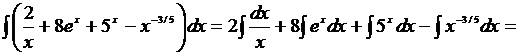
= 


Домашнее задание
 составить конспект
составить конспект
 решить
решить

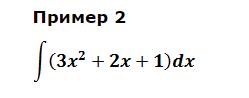
 фото прислать на электронную почту техникума kitdisttpop@mail.ua kitdisttpop@mail.ua. или VK https://vk.com/feed с полным названием ФИО студента, группа (например - Иванов И.И., ТЭЭО-19, Математика: алгебра и начала математического анализа, геометрия)
фото прислать на электронную почту техникума kitdisttpop@mail.ua kitdisttpop@mail.ua. или VK https://vk.com/feed с полным названием ФИО студента, группа (например - Иванов И.И., ТЭЭО-19, Математика: алгебра и начала математического анализа, геометрия)
КРИТЕРИИ ОЦЕНИВАНИЯ
Ответ оценивается отметкой «5», если:
· работа выполнена полностью;
· в логических рассуждениях и обосновании решения нет пробелов и ошибок;
· в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
· работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
· допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
· допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но учащийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
· допущены существенные ошибки, показавшие, что учащийся не обладает обязательными умениями по данной теме в полной мере.
Отметка «1» ставится в случае:
· полного незнания изученного материала, отсутствия элементарных умений и навыков.