Дисциплина: ЕН.01 Математика: алгебра и начала математического анализа, геометрия
Группа: ТЭЭО -19
Дата: 21.10. 2020
Преподаватель: Кулага Т.Ф.
Задание: Ф ото выполненной работы прислать по адресу: kitdistergo@mail.ua kitdisttpop@mail.ua. или https://vk.com/id596417775 личным сообщением
(Название файла с ответами: № занятия, дисциплина, группа, Фамилия, имя, студента).
Например, Иванов И.И., ТЭЭО -20-11, Математика: алгебра и начала математического анализа, геометрия
Сроки выполнения: 22.10.2020
Задания для дистанционного обучения будут выдаваться в день проведения занятия, согласно расписанию и подмен по адресу: https://s3320.nubex.ru/5989/ или VK https://vk.com/ ТЭЭО-20-11, https://vk.com/ ТПОП-19
Мотивация
«Метод решения хорош, если с самого начала мы можем предвидеть – и далее подтвердить это, - что, следуя этому методу, мы достигнем цели».
Готфрид Лейбниц
Тема занятия: «МЕТОДЫИНТЕГРИРОВАНИЯ НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА»
План
1. Повторение теоретического материала
2. Таблица интегралов
3. Основные методы вычисления неопределенного интеграла
Повторение теоретического материала
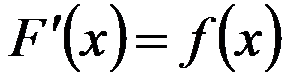(1)
Пример 1. Найти первообразную от функции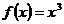 
. Из определения первообразной следует, что 
- первообразная функции 
, поскольку:
.
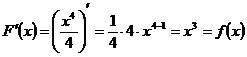Задача отыскания по данной функции ее первообразной решается не однозначно. В рассмотренном примере первообразной для функции 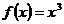является не только функция , но и, к примеру, 
и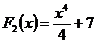 
и вообще 
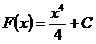(где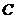 
- некоторая константа), что можно проверить дифференцированием данных функций.
Определение. Если функция 
является первообразной для функции , выражение 
называется неопределенным интегралом и обозначается символом 
. Таким образом можно записать:
(8.3)
— подынтегральная функция;
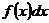— подынтегральное выражение;
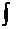— знак неопределенного интеграла;
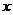— переменная интегрирования.
Свойства неопределенного интеграла
Основные методы вычисления неопределенного интеграла
Пусть требуется найти неопределенный интеграл , причем непосредственно подобрать первообразную не представляется возможным, но известно, что она существует. В этом случае применяются различные методы интегрирования, благодаря которым исходный интеграл можно привести к интегралу табличного вида. Рассмотрим некоторые из этих методов.
1. Метод непосредственного интегрирования. Используя свойства неопределенного интеграл, а также выполняя элементарные математические преобразования подынтегральной функции, исходный интеграл можно привести к неопределенному интегралу табличного вида.
Пример 2. Найти неопределенный интеграл 
.
Используя пятое свойство неопределенного интеграла, вынесем за знак интеграла постоянную 2. Затем, выполняя элементарные математические преобразования, приведем подынтегральную функцию к степенному виду:
. 
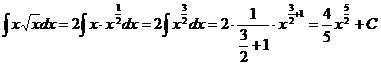2. Замена переменной. Пусть требуется найти неопределенный интеграл . Сделаем замену в подынтегральном выражении, положив 
, где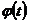 
— монотонная непрерывная функция, которая имеет непрерывную производную. Тогда 
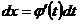. В этом случае имеет следующее равенство:
(8.9)
Пример 3. Найти неопределенный интеграл 
, используя метод замены переменной.
Сделаем замену переменной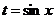 
, тогда 
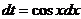. Исходный интеграл примет вид:
Таким образом, мы получили неопределенный интеграл табличного вида: степенная функция. Используя правило нахождения неопределенного интеграла от степенной функции (см. п.1 в таблице интегралов), найдем:
Сделав обратную замену, получим окончательный ответ:
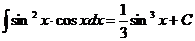
3. Интегрирование по частям. Пусть 
и 
— две дифференцируемые функции от переменной 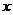. Тогда дифференциал произведения вычисляется по формуле:
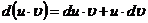(8.10)
Интегрируя, получим:
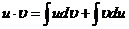(8.11)
Отсюда:
(8.12)
Последняя формула называется формулой интегрирования по частям. 
Пример 4. Найти неопределенный интеграл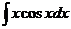 
, используя метод интегрирования по частям.
Введем следующие обозначения:
(8.13)
Тогда дифференцируя первое выражение и интегрируя второе, получим:
(8.14)
Теперь подставив в формулу (8.12) введенные нами обозначения (8.13) и (8.14), получим:
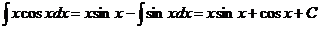
4. Интегралы от некоторых функций, содержащих квадратный трехчлен.
Рассмотрим следующие случаи:
а) В знаменателе интегрируемой функции квадратный трехчлен f(x) = 
.
Преобразуем его, выделив полный квадрат.
.
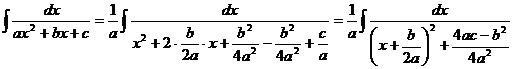Введем обозначение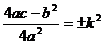 
. Таким образом, данный интеграл приобретает вид:
.
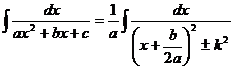Сделаем в последнем интеграле замену переменной:
, 
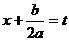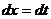
Получим:
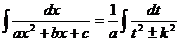. Это – табличный интеграл.
Пример 5.
Вычислить интеграл:
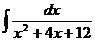
б) Подынтегральная функция имеет вид 
. Произведем тождественные преобразования:
Таким образом, исходный интеграл можно представить в виде суммы:
Как вычислять второй интеграл, мы рассмотрели в пункте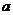 
; обозначим его через 
. В первом интеграле сделаем замену переменной:
, 
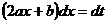
Таким образом:
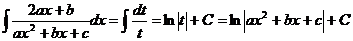
Окончательно получим:
Домашнее задание
составить конспект
Решить п ример:
фото прислать на электронную почту техникума kitdisttpop@mail.ua kitdisttpop@mail.ua. или VK https://vk.com/feed с полным названием ФИО студента, группа (например - Иванов И.И., ТЭЭО-19, Математика: алгебра и начала математического анализа, геометрия)
КРИТЕРИИ ОЦЕНИВАНИЯ
Ответ оценивается отметкой «5», если:
· работа выполнена полностью;
· в логических рассуждениях и обосновании решения нет пробелов и ошибок;
· в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
· работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
· допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
· допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но учащийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
· допущены существенные ошибки, показавшие, что учащийся не обладает обязательными умениями по данной теме в полной мере.
Отметка «1» ставится в случае:
· полного незнания изученного материала, отсутствия элементарных умений и навыков.