Индивидуальные задания по курсу
«Теория вероятностей и математическая статистика»
Часть II
(Для студентов специальностей 7.080404, 7.080407, 7.091302)
Донецк, 2014
Министерство образования и науки Украины
Донецкий национальный университет
Пясецкая Т.Е.
Индивидуальные задания по курсу
«Теория вероятностей и математическая статистика»
Часть II
(Для студентов специальностей 7.080404, 7.080407, 7.091302)
Донецк, 2014
 |
Пясецкая Т.Е.
Индивидуальные задания по курсу «Теория вероятностей и математическая статистика», часть II. Донецк, ДонНУ, 2014г.
Настоящее методическое пособие предназначено для организации самостоятельной работы студентов, изучающих теорию вероятностей и математическую статистику, их подготовку к модульному контролю. Оно содержит тексты 16 вариантов индивидуального задания. Приведены решения задач одного из вариантов задания. Эти решения могут быть использованы как методические рекомендации студентам в процессе выполнения и оформления индивидуальных заданий.
Приведен список рекомендуемой литературы
Утверждено к печати Ученым Советом физико-технического факультета Донецкого Национального Университета.
 |
Индивидуальное задание посвящено дискретным и непрерывным случайным величинам.
Студент должен уметь составлять законы распределения дискретной случайной величины, строить функцию распределения, вычислять числовые характеристики дискретной случайной величины; строить функцию распределения и плотность вероятности непрерывной случайной величины, применять свойства случайной величины к решению задач, вычислять математическое ожидание и дисперсию случайных величин, имеющих плотность вероятности.
Вариант 0
1.Грани двух тетраэдров пронумерованы числами 1-4. тетраэдры бросаются на горизонтальную плоскость. Пусть Х- меньшее из чисе5л, оказавшееся на гранях, прилегающих к плоскости, после обретения тетраэдрами покоя. Найдите: а) закон распределения случайной величины Х; б) функцию распределения этой случайной величины.
Решение. Исход эксперимента – это пара (i,k), где i – одно из значений чисел 1, 2, 3, 4, которое появится на грани, прилегающей к плоскости первого тетраэдра. Всего пар (i,k) 
.
Случайна величина Х принимает значения 1, 2, 3, 4.
Х = 1, если i = 1, k = 1, 2, 3, 4 или i = 2, 3, 4, k = 1. Всего 7 исходов из 16 возможных. P(X=1) = 
.
X = 2 в вариантах (2,2), (2,3), (2,4), (3,2), (4,2) – 5 исходов из 16 возможных P(X=2) =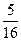 
.
Х = 3 – (3,3), (3,4), (4,3) – 3 исхода из 16. P(X=3) =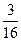 
.
Х = 4 – (4,4) – 1 вариант из 16. P(X=4)=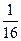 
.
а) Закон распределения случайной величины
Х:
| хk | ||||
| pk |
|
|
|
|
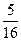
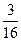
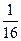
б) Функция распределения случайной величины Х.
По определению F(x) = P(X < x),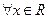 
. Обозначим на числовой оси значения, которые принимает случайная величина Х.
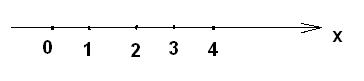
Пусть х < 1. Левее числа 1 нет ни одного значения случайной величины Х. Поэтому F(x) = 0, если х < 1.
Пусть х = 1. по определению F(1) = P(X < 1) = 0. Поэтому F(1)=0.
Итак, F(x) = 0, если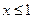 
.
Пусть 
. Левее любого фиксированного числа х из этого промежутка есть только одно значение случайной величины Х = 1. P(X=1) = . Поэтому F(x) = , если (о включении правого конца промежутка 
мы уже обращали внимание на примере предыдущего интервала).
Пусть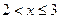 
. Левее любой точки, принадлежащей этому промежутку, есть два значения случайной величины Х: 1 и 2.
P(X=1 или Х=2) = P(X=1) + P(X=2) = + = 
.
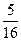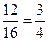Пусть 
. Левее любой точки, взятой из этого промежутка, есть три значения случайной величины Х: 1, 2, 3.
P(X=1 или Х=2 или Х=3) = + + = 
.
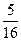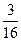И наконец, если х > 4, то в промежуток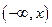 
попадают все значения случайной величины Х. поэтому принять случайной величине какое-либо из возможных значений – событие достоверное и F(x) = 1, если x > 4.
Функции распределения случайной величины Х:
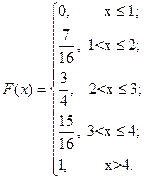
Построим график функции распределения
2. Выпущено 100 лотерейных билетов, на 10 из которых выпадает выигрыш по 20 денежных единиц, на 5 – по 50 денежных единиц, а остальные билеты невыигрышные. Пусть случайная величина Х – размер выигрыша, который выпадает владельцу двух билетов. Найдите: а) закон распределения Х; б) числовые характеристики этой случайной величины; в) P(X>0).
Решение. Случайная величина Х может принимать значение 0, 20, 40, 50, 70, 100. подсчитаем вероятности, соответствующие этим значением. Пусть исход эксперимента (i,k), где i,k = 0, 20, 50. Тогда P(X=0) = P(i=0, k=0) =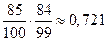 
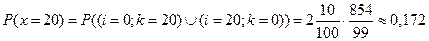
P(X = 40) = P(i = 20, k = 20) =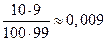 
P(X = 50) = P((i = 0, k = 50)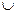 
(i = 50, k = 0)) = 
P(X = 70) = P((i = 20, k = 50) 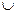(i = 50, k = 20)) =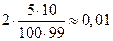 
P(X = 100) = P(i = 50, k = 50) =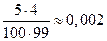 
Составим закон распределения случайной величины Х:
| xk | ||||||
| pk | 0,721 | 0,172 | 0,009 | 0,086 | 0,01 | 0,002 |
б) По определению математического ожидания случайной величины Х
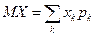
Поэтому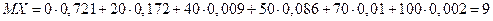 
Для нахождения дисперсии DX воспользуемся свойством 
. 
. 
. 
.
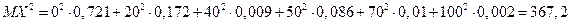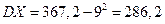в) P(X > 0) = 1 - P(X = 0) = 0,289.
3.Экзаменатор задает студенту дополнительные вопросы. Вероятность того, что студент ответит на любой заданный вопрос – 0,7. преподаватель прекращает экзамен, как только студент ответит на заданный вопрос. Найдите: а) закон распределения случайной величины Х – числа дополнительных вопросов; б) 
; в) MX и DX.
Решение. А) Дискретная случайная величина Х – число заданных дополнительных вопросов, может принимать значения 1, 2, 3,...
Х = 1 тогда и только тогда, когда студент ответил на первый вопрос, Р(Х = 1) = 0,7.
Х = 2 тогда и только тогда, когда студент не ответил на первый вопрос и ответил на второй. Р(Х = 2) =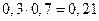 
и т.д.
Закон распределения этой случайной величины Х:
| xk | … | k | … | ||
| pk | 0,7 | 0,21 | 0,3k-10,7 | … |
- геометрическое распределения
б)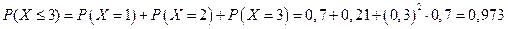 
.
в)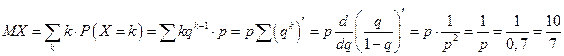 
.
.
Находим
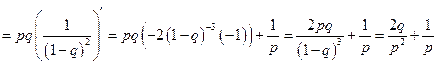
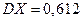
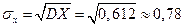
4. Дана функция распределения случайной величины Х:
Найдите: а) А и В; б) плотность f(x); в) 
; г) вероятность того, что в четырех независимых испытаниях случайная величина Х только два раза примет значения, принадлежащие отрезку [1;2].
Решение. А) Постоянные А и В найдем из свойств функции распределения: 
.
Имеем
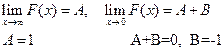
Следовательно,
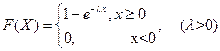
б) Плотность вероятности
в) 
г) по формуле Бернулли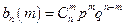 
В нашем случае n = 4, m = 2, p = 
Имеем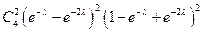 
.
5. Дана плотность вероятности случайной величины Х
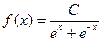
Найдите: а) постоянную С; б) функцию распределения F(x); в) вероятность 
.
Решение. Постоянную С находим из свойства плотности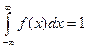 
. В нашем случае 
.
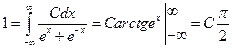б) Функцию распределения находим из равенства 
.
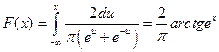в)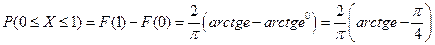 
.
6. Для нормально распределенной случайной величины Х с параметрами МХ = 10 и DX = 4 найдите вероятность того, что в результате испытания она примет значение, заключенное в интервале (12, 14).
Решение. Воспользуемся формулой
Подставим в эту формулу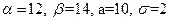 
. Получим 
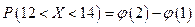. По таблице значений функции 
находим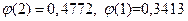 
. Искомая вероятность 
.
Вариант 1
1. По мишени производят три выстрела. Вероятность попадания при первом выстреле 0,1, при втором – 0,2, при третьем – 0,3. составьте закон распределения числа попаданий по мишени при трех выстрелах. Постройте функцию распределения этой случайной величины.
2. Среди 10 изделий одно бракованное. Чтобы найти бракованное изделие, берут наудачу изделие и проверяют его. Составьте закон распределения числа проверенных изделий Х. найдите числовые характеристики случайной величины Х.
3. Монету подбрасываю до тех пор, пока она не выпадет на сторону герб. Найдите: а) закон распределения случайной величины Х – числа подбрасываний монеты; б) 
; в) 
.
4. Случайная величина Х задана функцией распределения
.
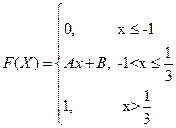Найдите: а) А и В; б) плотность f(x); в)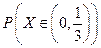 
.
5.Задана плотность распределения случайной величины Х
.
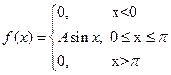Найдите: а) А; б) функцию распределения F(х); в) числовые характеристики случайной величины Х.
6. Для нормально распределенной случайной величины Х найдите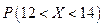 
, если МХ = 10 и DX = 4.
Вариант 2
1. Производится 4 независимых выстрела по мишени. Вероятность попадания при первом выстреле 0,25. Постройте закон распределения случайной величины Х - числа попаданий в мишень. Найдите наивероятнейшее число попаданий. Постройте функцию распределения этой случайной величины.
2. Вероятность того, что покупатель совершит покупку в магазине – 0,4. составьте закон распределения случайной величины Х – числа покупателей, совершивших покупку, если магазин посетило три покупателя. Найдите: а) числовые характеристики случайной величины Х; б)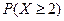 
.
3. Игральную кость подбрасывают до тех пор пока не выпадет на верхней грани шестерка. Найдите: а) закон распределения случайной величины Х – числа подбрасывания кости; б) ; в) 
.
4. Случайная величина Х задана функцией распределения
.
Найдите: а) А и В; б) плотность f(x); в) 
.
5. Плотность распределения случайной величины имеет вид
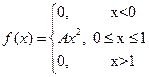
Найдите: а) А; б) функцию распределения F(х); в)
6. Для нормально распределенной случайной величины Х найдите 
, если МХ = 20 и 
.
Вариант 3
1. Вероятность поражения вирусным заболеванием куста земляники равна 0,2. составьте закон распределения числа кустов земляники, зараженных вирусом, из четырех посаженных. Постройте функцию распределения этой случайной величины.
2. На пути движения автомобиля 6 светофоров, каждый из которых разрешает или запрещает двигаться автомобилю с вероятностью 0,5. составьте закон распределения случайной величины Х – числа светофоров, мимо которых проехал автомобиль без остановки. Найдите числовые характеристики этой случайной величины.
3. Снайпер стреляет по замаскированному противнику до первого попадания. Вероятность промаха при отдельном выстреле 0,3. пусть случайная величина Х – число выстрелов до первого попадания. Найдите: а) закон распределения случайной величины Х; б) Р(Х>1); в) .
4. Функция распределения случайной величины Х имеет вид
Найдите: а) А; б) плотность f(x); в)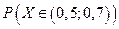 
.
5. Плотность распределения случайной величины имеет вид
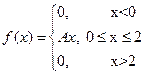
Найдите: а) А; б) функцию распределения F(х); в)
6. Случайные величины X и Y независимы и распределены по закону Пуассона с параметрами a = 0,3, и b = 1,2. Найдите M(X+Y) и D(X+Y).
Вариант 4
1. Стрелок ведет стрельбу по целее с вероятностью попадания при каждом выстреле 0,2. За каждое попадание он получает 5 очков, а в случае промаха очков ему не начисляют. Составьте закон распределения числа очков Х, полученных стрелком за 3 выстрела. Постройте функцию распределения случайной величины Х.
2. Пусть Х – количество появлений числа 5 на верхней грани игрального кубика при двукратном его подбрасывании. Найдите закон распределения случайной величины Х и её числовые характеристики.
3. Вероятность наступления события А в каждом испытании равна 0,6. Испытания производятся до первого появления события А. найдите: а) закон распределения случайной величины Х – числа испытаний до первого наступления события А; б) 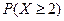; в) числовые характеристики случайной величины.
4. Дана функция распределения случайной величины Х
Найдите: а) А; б) плотность f(x); в) 
.
5. Случайная величина Х имеет плотность
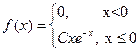
Найдите: а) С; б) F(х); в)
6. Случайные величины X и Y независимы и распределены по закону Пуассона с параметрами a = 1,7, и b = 2,1. Найдите M(X+Y) и D(X+Y).
Вариант 5
1. Контрольная работа состоит из трех вопросов. На каждый вопрос приведено 4 ответа, один из которых правильный. Составьте закон распределения числа правильных ответов Х при простом угадывании. Постройте функцию распределения случайной величины Х.
2. Произведено два выстрела в мишень. Вероятность попадания в мишень первым стрелком равна 0,8, вторым – 0,7. Каждый стрелок делает по одному выстрелу. Составьте закон распределения случайной величины Х – числа распределения случайной величины Х – числа попаданий в мишень. Найдите: а) числовые характеристики случайной величины Х; б)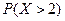 
.
3. Радист вызывает корреспондента, причем каждый последующий вызов производится лишь в том случае, если предыдущий вызов не принят. Вероятность того, что корреспондент примет вызов, равна 0,4. Составьте закон распределения числа вызовов Х, если их количество не ограничено. Найдите: а) 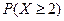; б) а) числовые характеристики случайной величины Х.
4. Задана функция распределения случайной величины Х
Найдите: а) А и В; б) плотность f(x); в) 
.
5. Случайная величина Х имеет плотность
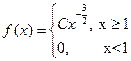
Найдите: а) С; б) F(х); в) .
6. Найдите математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины Х, распределенной по биномиальному закону, если n = 10, p = 0,4.
Вариант 6
1. Произведено два выстрела по мишени. Вероятность попадания в мишень первым стрелком равна 0,8, вторым – 0,7. Составьте закон распределения случайной величины Х – числа попаданий по мишени, если каждый из стрелков сделал по одному выстрелу. Найдите функцию распределения этой случайной величины.
2. В среднем по 10% договоров страховая компания выплачивает страховые суммы в связи с наступлением страхового случая. Составьте закон распределения числа таких договоров среди наудачу выбранных четырех. Вычислите числовые характеристики этой случайной величины.
3. Независимые опыты продолжаются до первого успеха, после чего прекращаются. Вероятность успеха в каждом опыте равна 0,7. Составьте закон распределения числа опытов Х. Найдите: а) ; б) .
4. Случайная величина Х задана своей функцией распределения
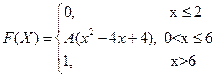
Найдите: а) А; б) плотность f(x); в)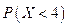 
.
5. Случайная величина Х имеет плотность
Найдите: а) С; б) F(х); в) .
6. Нормальное распределение случайной величины Х имеет МХ = -1 и DX = 9. Запишите плотность распределения этой случайной величины.
Вариант 7
1. Найдите закон распределения числа пакетов трех акций, по которым владельцем будет получен доход, если вероятность получения дохода по каждому из них равна соответственно 0,5, 0,6, 0,7. Постройте функцию распределения этой случайной величины.
2. Вероятность попадания в цель при первом выстреле равна 0,8 и уменьшается с каждым выстрелом на 0,1. Составьте закон распределения случайной величины Х – числа попаданий в цель, если сделано три выстрела. Найдите: а) числовые характеристики случайной величины Х; б)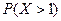 
.
3. Некий азартный игрок собирается играть в такую игру. Бросает две игральные кости. Если при этом выпадает хотя бы одна шестерка, он выигрывает 100 грн. Во всех остальных случаях он проигрывает 25 грн. Игра продолжается до тех пор пока не выпадет хотя бы одна шестерка на одной из граней. Найдите: а) закон распределения выигрыша игрока; б) числовые характеристики выигрыша игрока.
4. Случайная величина Х задана своей функцией распределения
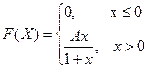
Найдите: а) А; б) плотность f(x); в) 
.
5. Случайная величина Х имеет плотность
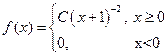
Найдите: а) С; б) плотность f(x); в) числовые характеристики случайной величины Х.
6. Найдите математическое ожидание и дисперсию случайной величины Х, распределенной по биномиальному закону, если n = 30, p = 0,1.
Вариант 8
1. На выставке из 10 телевизоров 4 оказались фирмы «Сони». Наудачу для осмотра выбрано 3. Составьте закон распределения случайной величины Х – числа телевизоров фирмы «Сони» среди отобранных. Постройте функцию распределения этой случайной величины.
2. В билете три задачи. Вероятность правильного решения первой задачи равна 0,9, второй – 0,8, третьей – 0,7. составьте закон распределения случайной величины Х – числа правильно решенных задач в билете. Найдите: а) числовые характеристики случайной величины Х; б) .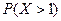
3. Вероятность того, что денежный автомат при опускании монеты сработает правильно, равна 0,97. составьте закон распределения числа опусканий монет в автомат до первого правильного срабатывания монеты. Найдите: а) числовые характеристики этой случайной величины Х; б) 
.
4. Случайная величина Х задана своей функцией распределения
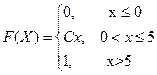
Найдите: а) С; б) плотность f(x); в)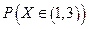 
.
5. Задана плотность распределения случайной величины Х
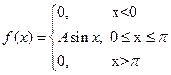
Найдите: а) А; б) функцию распределения F(х); в) числовые характеристики этой случайной величины Х.
6. Нормально распределенная случайная величина Х имеет МХ=0 и DX = 1. Запишите плотность распределения этой случайной величины.
Вариант 9
1. В магазине продается 5 отечественных и 3 импортных телевизора. Составьте закон распределения случайной величины Х – числа импортных телевизоров из четырех наудачу выбранных. Найдите функцию распределения этой случайной величины.
2. Трое студентов сдают экзамен по теории вероятностей. Вероятность того, что первый студент сдаст экзамен равна 0,9, второй – 0,85, третий – 0,8. Пусть Х – числа студентов, которые могут сдать экзамен по теории вероятностей. Составьте закон распределения случайной величины Х. Найдите: а) числовые характеристики случайной величины Х; б) .
3. Ребенок бьет молотком по дорогой игрушке до тех пор пока она полностью не разрушится. Вероятность уничтожения игрушки при одном ударе равна 0,1. Найдите: а) закон распределения числа ударов Х, необходимых для полного разрушения игрушки; б) числовые характеристики случайной величины Х.
4. Случайная величина Х задана своей функцией распределения
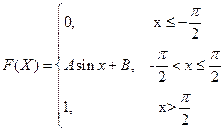
Найдите: а) А и В; б) плотность f(x); в) 
.
5. Случайная величина Х имеет плотность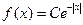 
. Найдите: а) С; б) F(х); в) .
6. Найдите математическое ожидание и дисперсию случайной величины Х, распределенной по биномиальному закону, если n = 15, q= 0,8.
Вариант 10
1. Экзаменатор задает студенту вопросы, пока тот правильно отвечает. Как только число правильных ответов достигает четырех либо студент отвечает неправильно, экзаменатор прекращает задавать вопросы. Вероятность правильно ответить на один вопрос равна 2/3. Составьте закон распределения случайной величины Х – числа заданных студенту вопросов. Найдите функцию распределения случайной величины Х.
2. Вероятность того, что футболист реализует одиннадцатиметровый штрафной удар равна 0,9. футболист делает три таких удара. Постройте закон распределения случайной величины Х – числа реализованных штрафных. Найдите: а) числовые характеристики случайной величины Х; б) .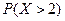
3. Игральную кость подбрасывают до первого появления на верхней грани пятерки. Составьте закон распределения случайной величины Х – числа подбрасываний кости. Найдите: а) ; б) числовые характеристики случайной величины Х.
4. Случайная величина Х задана своей функцией распределения
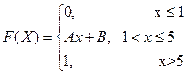
Найдите: а) А и В; б) плотность f(x); в)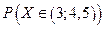 
.
5. Случайная величина Х имеет плотность
Найдите: а) С; б) F(х); в) числовые характеристики случайной величины Х.
6. Нормально распределенная случайная величина Х имеет МХ = -2 и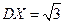 
. Запишите6 плотность распределения этой случайной величины.
Вариант 11
1. Вероятность работы из четырех комбайнов без поломок в течение определенного времени равна 0,9. Составьте закон распределения случайной величины Х – число комбайнов, работавших безотказно. Постойте функцию распределения этой случайной величины.
2. На конноспортивных соревнованиях необходимо преодолеть четыре препятствия с вероятностями 0,9, 0,8, 0,7, 0,6. При первой неудаче спортсмен в дальнейших состязаниях не участвует. Составьте закон распределения случайной величины Х – числа взятых препятствий.
3. Имеется n лампочек, каждая из них с вероятностью р имеет дефект. Лампочка ввинчивается в патрон и включается ток. При включении тока дефектная лампа сразу же перегорает, после чего заменяется другой. Пусть Х – число испробованных лампочек. Найдите: а) закон распределения случайной величины Х; б) МХ, DX.
4. Дана функция распределения Случайной величины Х
Найдите: а) А; б) плотность f(x); в)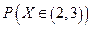 
.
5. Случайная величина Х имеет плотность
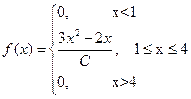
Найдите: а) С; б) F(х); в) МХ, DX.
6. Случайные величины X и Y независимы и распределены по закону Пуассона с параметрами a = 5, и b = 2 соответственно. Найдите M(X+Y) и D(X+Y).
Вариант 12
1. Вероятность того, что покупатель совершит покупку – 0,4. Составьте закон распределения случайной величины Х – числа покупателей, сделавших покупку, если магазин посетило три покупателя. Постройте функцию распределения этой случайной величины.
2. Найдите закон распределения случайной величины Х – числа пакетов трех акций, по которым владельцем будет получен доход, если вероятность получения дохода по каждому из них равна соответственно 0,5, 0,6, 0,7. Найдите: а) числовые характеристики случайной величины Х; б) .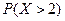
3. Монету подбрасывают до тех пор пока она не выпадет на сторону решка. Пусть Х – число подбрасываний монеты до первого появления решки. Найдите: а) закон распределения случайной величины Х; б) 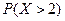; в) числовые характеристики случайной величины Х.
4. Случайная величина Х задана функцией распределения
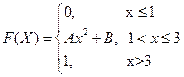
Найдите: а) А и В; б) плотность f(x); в) 
.
5. Случайная величина Х имеет плотность
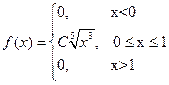
Найдите: а) С; б) F(х); в) числовые характеристики случайной величины Х.
6. Для нормально распределенной случайной величины Х найдите 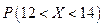, если МХ = 10 и DX = 4.
Вариант 13
1. Покупатель посещает магазин для приобретения нужного товара. Вероятность того, что товар имеется в определенном магазине, равна 0,4. Составьте закон распределения случайной величины Х — число магазинов, которые посетил покупатель из четырех возможных. Найдите функцию распределения случайной величины Х.
2. Из 10 телевизоров, имеющихся на выставке, 4 оказались фирмы «Сони». Наудачу для осмотра выбрано три. Составьте закон распределения случайной величины Х — числа телевизоров фирмы «Сони» среди трех отобранных. Найдите:
а) числовые характеристики этой случайной величины;
б) Р(
).
3. Стрелок производит выстрелы до первого попадания в цель. Вероятность попадания в цель при одном выстреле равна 0,7. Составьте закон распределения случайной величины Х — числа выстрелов, сделанных стрелком. Найдите:
а) числовые характеристики случайной величины Х;
б) Р(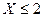
).
4. Случайная величина Х задана функцией распределения
Найдите: а) А; б) плотность 
; в) 
.
5. Случайная величина Х имеет плотность
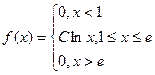
Найдите: а) С; б) F(x); в) числовые характеристики случайной величины Х.
6. Рост взрослой женщины является случайной величиной, распределенный по нормальному закону с параметрами а=164см,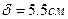 
. Найдите плотность вероятности и функцию распределения этой случайной величины.
Вариант 14
1. Имеется три ящика с деталями. В первом — 6 стандартных и 4 бракованных; во втором — 8 стандартных и 2 бракованных, в третьем —5 стандартных и 5 бракованных. Из каждого ящика берут по одной детали. Пусть случайная величина Х – число стандартных деталей среди трех наудачу взятых. Постройте закон распределения этой случайной величины.
2. В магазине продается 5 отечественных и 3 импортных телевизора. Составьте закон распределения случайной величины Х – числа импортных из 4 наудачу выбранных телевизоров. Найдите: а) числовые характеристики этой случайной величины;
б) Р(
).
3. Игральную кость подбрасывают до тех пор пока на верхней грани кубика не выпадет двойка. Составьте закон распределения случайной величины Х – числа подбрасываний кости; Найдите: а) числовые характеристики случайной величины Х;
б) Р().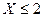
4. Случайная величина Х задана функцией распределения
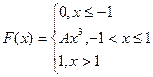
Найдите: а) А; б) плотность ; в)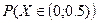 
.
5. Случайная величина имеет плотность
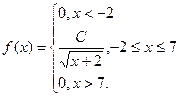
Найдите: а) С; б) F(x); в) числовые характеристики случайной величины Х.
6. Нормально распределенная случайная величина имеет параметры а=3,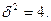 
Запишите плотность этой случайной величины.
Вариант 15
1. Трое студентов сдают экзамен по теории вероятности. Вероятность того, что первый студент сдаст экзамен равен 0,9, второй – 0,85, третий – 0,8. Случайная величина Х – число студентов, сдавших экзамен. Постройте закон распределения этой случайной величины Х и ее функцию распределения.
2. Произведено три независимых выстрела по мишени. Вероятность попадания в мишень при каждом выстреле равна 0,4. Случайная величина Х–число попаданий. Найдите:
а) числовые характеристики этой случайной величины;
б) Р().
3. Баскетболист кидает мяч в корзину до первого попадания. Составьте закон распределения случайной величины Х – число бросков, сделанных баскетболистом, если вероятность попадания в корзину при одном броске 0,3. Найдите: а) числовые характеристики случайной величины Х; б) Р(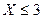
).
4. Случайная величина Х задана функцией распределения
Найдите: а) А и В; б) плотность ; в)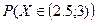 
.
5. Случайная величина имеет плотность
Найдите: а) А; б) F(x); в) числовые характеристики случайной величины Х.
6. Рост взрослого мужчины является случайной величиной, распределенный по нормальному закону. Пусть а=170, 
Найдите f(x) и F(x).
Список литературы
1. Гихман И. И. Скороход М. И. Теория вероятностей и математическая статистика. Киев. Вища школа, 2000.
2. Теория вероятностей. Сборник задач. Под редакцией Скорохода А. В., Киев, 1990г. 384с.
3. Гмурман В. Е. Теория вероятностей и математическая статистика. М. «Высшая школа», 2000г. 479с
4. Гмурман В. Е. Теория вероятностей и математическая статистика. М. «Высшая школа», 2002г. 338с
5. Пясецкая Т. Е. Теория вероятностей и математическая статистика. Задачи и методические рекомендации к их решению. (Для студентов специальностей 7080404, 7080407, 7091302). Донецк, 2008г.