Методические указания по контрольному заданию.
курс «Защита информации»
Задание
1. Запишите первые семь букв своей фамилии латинскими буквами в привычном вам виде. Для фамилий короче 7 букв недостающие символы считайте пробелами.
2. Переведите полученные 7 символов в двоичный вид с помощью таблицы ASCII (Приложение 1).Обратите внимание, коды символов представлены в таблице в шестнадцатеричной форме.
3. Рассчитайте простейший хэш-код от полученных 7 символов – ротационный XOR
4. С помощью алгоритма шифрования DEA (описанного в стандарте DES) произведите шифрование полученного 8-ми байтного блока информации:
– В качестве пароля используйте набор из 7 разных букв, также переведенных в двоичную форму при помощи таблицы ASCII.
– Для шифрования используйте только 4 раунда шифрования из предусмотренных стандартом 16-ти.
– Записывайте все промежуточные данные (значения всех блоков в приведенных блок-схемах для каждого раунда).
6. Результирующие 64 бита разбейте на 8 байтов и переведите в символы в соответствии с таблицей ASCII.
Теоретические сведения
Простейшие хэш-функции: XOR и ротационный XOR
Все хэш-функции выполняются следующим образом. Входное значение (сообщение, файл и т.п.) рассматривается как последовательность n-битных блоков. Входное значение обрабатывается последовательно блок за блоком, и создается m-битное значение хэш-кода.
Одним из простейших примеров хэш-функции является побитный XOR каждого блока:
Сi = bi1  bi2
bi2  ...
...  bik
bik
где:
Сi - i-ый бит хэш-кода, 1  i
i  n.
n.
k - число n-битных блоков входа.
bij - i-ый бит в j-ом блоке.
 - операция XOR.
- операция XOR.
В курсовом проекте блоками будут являться символы фамилии, представленные в двоичном виде. В результате получается хэш-код длины n, известный как продольный избыточный контроль. Это самый простейший хэш-код.
Часто при использовании подобного продольного избыточного контроля для каждого блока выполняется однобитный циклический сдвиг после вычисления хэш-кода. Такую операцию называют «ротационный XOR». Это можно описать следующим образом.
- Установить n-битный хэш-код в ноль.
- Для каждого n-битного блока данных выполнить следующие операции:
- сдвинуть циклически текущий хэш-код влево на один бит;
- выполнить операцию XOR для очередного блока и хэш-кода.
Это даст эффект "случайности" входа и уничтожит любую регулярность, которая присутствует во входных значениях.
Стандарт шифрования DES
Стандарт шифрования DES (Data Encryption Standard) был разработан в 1970-х годах, он базируется на алгоритме DEA.
Исходные идеи алгоритма шифрования данных DEA (data encryption algorithm) были предложены компанией IBM еще в 1960-х годах и базировались на идеях, описанных Клодом Шенноном в 1940-х годах. Первоначально эта методика шифрования называлась lucifer (разработчик Хорст Фейштель, название dea она получила лишь в 1976 году. Lucifer был первым блочным алгоритмом шифрования, он использовал блоки размером 128 бит и 128-битовый ключ. По существу этот алгоритм являлся прототипом DEA. В 1986 в Японии (NIT) разработан алгоритм FEAL (Fast data Encipherment ALgorithm), предназначенный для использования в факсах, модемах и телефонах (длина ключа до 128 бит). Существует и ряд других разработок.
DEA (ANSI x3.92-1981) оперирует с блоками данных размером 64 бита и использует ключ длиной 56 бит. Такая длина ключа соответствует 1017 комбинаций, что обеспечивало до недавнего времени достаточный уровень безопасности. В дальнейшем можно ожидать расширения ключа до 64 бит (например, LOKI) или вообще замены DES другим стандартом.
Входной блок данных, состоящий из 64 бит, преобразуется в выходной блок идентичной длины. Ключ шифрования должен быть известен, как отправляющей так и принимающей сторонам. В алгоритме широко используются перестановки битов текста.
Вводится функция f, которая работает с 32-разрядными словами исходного текста (А) и использует в качестве параметра 48-разрядный ключ (J). Схеме работы функции f показана на рис. 1.1. Сначала 32 входные разряда расширяются до 48, при этом некоторые разряды повторяются. Схема этого расширения показана ниже (номера соответствуют номерам бит исходного 32-разрядного кода).
Для полученного 48-разрядного кода и ключа выполняется операция исключающее ИЛИ (XOR). Результирующий 48-разрядный код преобразуется в 32-разрядный с помощью S-матриц. На выходе S-матриц осуществляется перестановка согласно схеме показанной ниже (числа представляют собой порядковые номера бит).
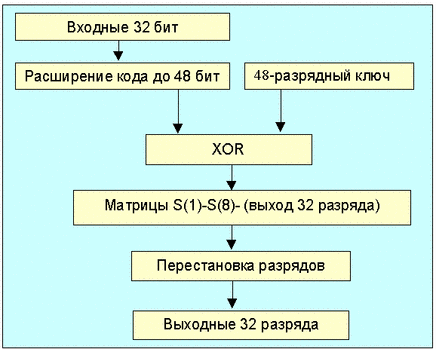
Рис. 1.1. Алгоритм работы функции f
Преобразование начинается с перестановки бит (IP itial Permutation) в 64-разрядном блоке исходных данных. 58-ой бит становится первым, 50-ый вторым и т.д. Схема перестановки битов показана ниже.
Полученный блок делится на две 32-разрядные части L0 и R0. Далее 16 раз повторяются следующие 4 процедуры:
- Преобразование ключа с учетом номера итерации i (перестановки разрядов с удалением 8 бит, в результате получается 48-разрядный ключ)
· Пусть A=Li, а J реобразованный ключ. С помощью функции f(A,J) генерируется 32-разрядный выходной код.
· Выполняется операция XOR для Ri f(A,J), результат обозначается Ri+1.
· Выполняется операция присвоения Li+1=Ri.
Структурная схема реализации алгоритма DEA показана на рис. 1.2.
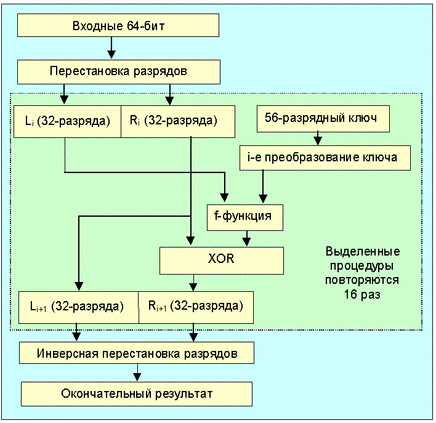
Рис. 1.2. Структурная схема реализации алгоритма DEA
Инверсная перестановка разрядов предполагает следующее размещение 64 бит зашифрованных данных (первым битом становится 40-ой, вторым 8-ой и т.д.).
S-матрицы представляют собой таблицы содержащие 4-ряда и 16 столбцов. Набор матриц приведен в Приложении 2. Матрица S(1) представлена ниже (эта матрица, так же как и те, что приведены в Приложении 2, являются рекомендуемыми).
| № | ||||||||||||||||
Исходный 48-разрядный код делится на 8 групп по 6 разрядов. Первый и последний разряд в группе используется в качестве адреса строки, а средние 4 разряда качестве адреса столбца. В результате каждые 6 бит кода преобразуются в 4 бита, а весь 48-разрядный код в 32-разрядный (для этого нужно 8 S-матриц). Существуют разработки, позволяющие выполнять шифрование в рамках стандарта DES аппаратным образом, что обеспечивает довольно высокое быстродействие.
Преобразования ключей Kn (n=1,…,16; Kn = KS(n,key), где n омер итерации) осуществляются согласно алгоритму, показанному на рис. 1.3.
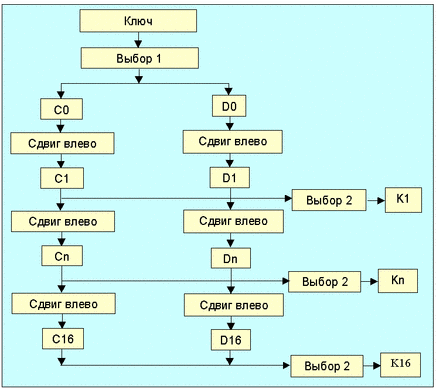
Рис. 1.3. Алгоритм вычисления последовательности ключей Kn
Для описания алгоритма вычисления ключей Kn (функция KS) достаточно определить структуру ыбора 1 ыбора 2а также задать схему сдвигов влево (табл. 1.2). ыбора 1 ыбора 2редставляют собой перестановки битов ключа (PC-1 и PC-2; табл. 1.1). При необходимости биты 8, 16,…, 64 могут использоваться для контроля четности.
Для вычисления очередного значения ключа таблица делится на две части С0 и D0. В С0 войдут биты 57, 49, 41,…, 44 и 36, а в D0, 55, 47,…, 12 и 4. Так как схема сдвигов задана (табл. 1.2) C1,D1; Cn, Dn и так далее могут быть легко получены из C0 и D0. Так, например, C3 и D3 получаются из C2 и D2 циклическим сдвигом влево на 2 разряда.
Таблица 1.1
| PC-1 (Выбор 1) | PC-2 (Выбор 2) | |||||||||||
Таблица 1.2
| Номер итерации | Число сдвигов влево |
Приложение 1. Таблица ASCII
| Код (Hex) | Символ | Код (Hex) | Символ | Код (Hex) | Символ | Код (Hex) | Символ | Код (Hex) | Символ | Код (Hex) | Символ |
| Пробел | . | @ | P | ' | p | ||||||
| ! | A | Q | a | q | |||||||
| " | B | R | b | r | |||||||
| # | C | S | c | s | |||||||
| $ | D | T | d | t | |||||||
| % | E | U | e | u | |||||||
| & | F | V | f | v | |||||||
| ' | G | W | g | w | |||||||
| ( | H | X | h | x | |||||||
| ) | I | Y | i | y | |||||||
| 2A | * | 3A | 4A | J | 5A | Z | 6A | j | 7A | z | |
| 2B | + | 3B | : | 4B | K | 5B | [ | 6B | k | 7B | { |
| 2C | , | 3C | ; | 4C | L | 5C | \ | 6C | l | 7C | | |
| 2D | - | 3D | < | 4D | M | 5D | ] | 6D | m | 7D | } |
| 2E | . | 3E | > | 4E | N | 5E | ^ | 6E | n | 7E | ~ |
| 2F | / | 3F | ? | 4F | O | 5F | _ | 6F | o | 7F | DEL |
Приложение 2. Матрицы S(x)
| S 1 | |||||||||||||||||
| S 2 | |||||||||||||||||
| S 3 | |||||||||||||||||
| S 4 | |||||||||||||||||
| S 5 | |||||||||||||||||
| S 6 | |||||||||||||||||
| S 7 | |||||||||||||||||
| S 8 | |||||||||||||||||