Лекция № 3.
Цель лекции: научиться строить линию пресечения поверхностей вращения с плоскостью.
Поверхности вращения составляют один из классов кривых поверхностей.
Кривой поверхностью называется геометрическое место (множество) последовательных положений линии, движущейся в пространстве.
Всякую поверхность можно рассматривать как образованную движением линии l по некоторой кривой m (рис.1). Линия l, образующая поверхность называется образующей, а линия m по которой движется образующая – направляющей.
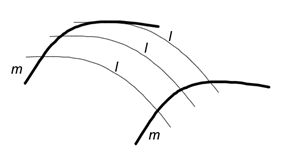
Рисунок 1 – Схема образования поверхности
Поверхности вращения образуются при вращении образующей l вокруг заданной оси i (рис. 2). При вращении образующей l каждая ее точка описывает окружность с центром О на оси вращения i. Плоскости этих окружностей перпендикулярны к i и, следовательно, взаимно параллельны и называются параллелями поверхности. Параллель с самым большим диаметром называется экватором, а с самым малым горлом. Линия пересечения поверхности вращения плоскостью параллельной плоскости проекций П и проходящей через ось вращения называется главным меридианом поверхности. Если i Ʇ П1, то все параллели поверхности, горло и экватор проецируются на П1 в истинную величину, а на П2 в отрезки прямых, перпендикулярные i2 – проекции оси i.
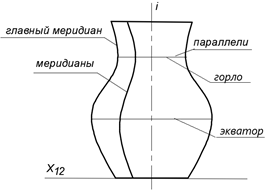
Рисунок 2 – Схема образования поверхности вращения
Линия пересечения проецирующей поверхности с плоскостью проекций П называется очерком проекций и является проекцией поверхности.
Задача. Построить линию пересечения прямого кругового конуса проецирующей плоскостью α (рис. 3).
На фронтальной плоскости проекций линия сечения конуса совпадает со следом проецирующей плоскости α. Плоскость α рассекает конус по всем образующим под углом к основанию меньшим, чем угол наклона образующих. Следовательно, в сечении конуса получается эллипс. Две вершины которого (точки 12 и 22) являются высшей и низшей точкамсечения, определяются пересечением следа плоскости α с очерком проекции конуса на плоскость П2. Эти точки называются характерными точками. К характерным точкам сечения относятся точки расположенные на очерковых образующих поверхности и точки, удаленные на максимальные расстояния от плоскости симметрии. Определяем, с помощью линий связи, проекции этих точек на плоскость П1 – 11 и 21.
Остальные точки сечения найдены с помощью плоскостей – посредников. Через т. 32 проводится вспомогательная плоскость параллельная основанию конуса. В сечении конуса образуется окружность, радиусом R равным расстоянию от оси конуса до его очерковой. Строим полученную окружность на горизонтальной проекции и опускаем на нее линию связи от точки 32, получаем горизонтальные проекции этой точки 31 и 31'. Точка 42 является точкой видимости сечения на профильной проекций конуса, поскольку принадлежит образующим конуса проецирующимися на профильную плоскость проекций в виде очерковых.
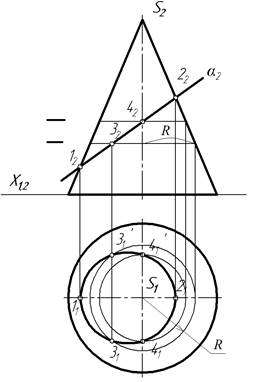
Рисунок 3 – Сечение конуса плоскостью
На видео показано построение сечения конуса рассечённого несколькими плоскостями.
В зависимости от направления секущей плоскости в сечении конической поверхности вращения могут получиться различные линии (кривые второго порядка) – коники.
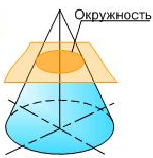
Если пересечь конус плоскостью перпендикулярной к оси конуса, то в сечении будет окружность (рис. 4а).
Если пересечь прямой круговой конус плоскостью, которая наклонена к оси конуса и пересекает все его образующие, то в сечении получится эллипс (рис. 4б).
Если пересечь тот же конус плоскостью параллельной одной из его образующих, то в сечении получится парабола (рис. 4в).
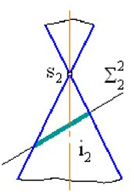
Если пересечь конус плоскостью, параллельной двум из его образующих (не проходящей через его вершину) то в сечении получится гипербола (рис. 4г).
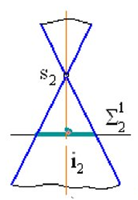
Секущая плоскость, проходящая через вершину, пересекает конус по образующим (рис. 4д).
Все сказанное, о сечениях конуса, будет справедливо и для наклонного конуса, кругового или эллиптического, т.е. для конуса поверхность которого в декартовых координатах выражается алгебраическим уравнением второй степени.
а)
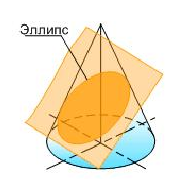
б)
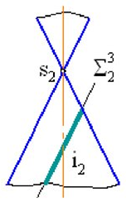
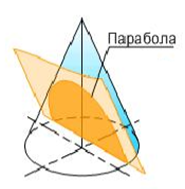
в)
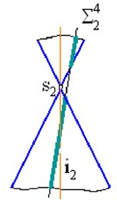
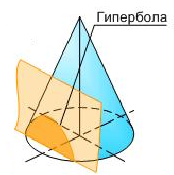
г)
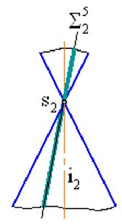
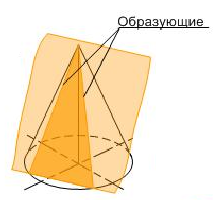
д)
Рисунок 4 – Сечения конуса – коники (а) окружность; б) эллипс; в) парабола;
г) гипербола; д) образующие)
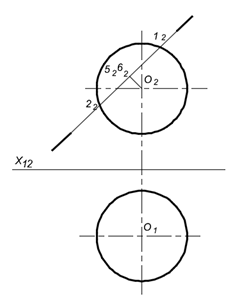
Задача. Построить сечение сферы фронтально-проецирующей плоскостью α.
Пусть дана сфера и фронтально-проецирующая плоскость α (рис.5). Окружность, по которой плоскость α пересекает сферу, спроецируется на П1 в виде эллипса. Две вершины этого эллипса (крайние точки - 11, 21) являются высшей и низшей точками сечения. Их фронтальная проекция определяется пересечением следа α2 плоскости с очерком проекции сферы на плоскость П2 – 12 и 22. Точки, отделяющие видимую часть горизонтальной проекции сечения от невидимой (т. 31 и 41), принадлежат экватору сферы – 32 и 42, а точки 5 и 6 определяют большую ось эллипса, длина которой равна диаметру окружности сечения, т.е. отрезок 51-61 равен отрезку 12-22. Остальные точки определяем способом вспомогательных плоскостей. Через точку проводим плоскость-посредник, параллельно экватору сферы. В сечении сферы этой плоскостью будет окружность, радиусом от оси сферы до её образующей. Строим эту окружность на плоскости П1 и по линии связи переносим на неё точку.
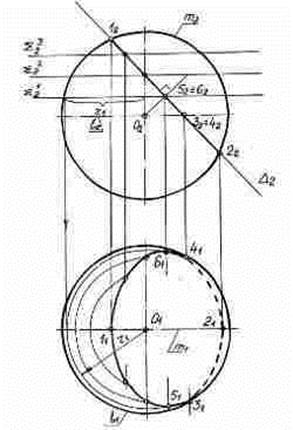
Рисунок 5 – Сечение сферы проецирующей плоскостью
На видео показано построение сечения сферы на трёх проекциях.