Глава 1. Уравнения, системы уравнений.
Линейные уравнения.
1. Уравнение первой степени вида 
, называется линейным уравнением. Где 
- переменные, числа 
и 
стоящие перед переменными называются коэффициентами, а 
и 
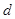- свободные члены. Запишем линейное уравнение
(1)
Для решения уравнения (1) перенесем переменные содержащие коэффициенты, в левую часть уравнения с положительным знаком, а свободные члены в правую часть уравнения с отрицательным знаком, получим уравнение вида
(2)
Пусть 
, а 
, тогда уравнение (2) будет иметь вид
(3)
Примеры.
1) Решить уравнение 
Перенесем неизвестные с коэффициентами в левую часть уравнения, а свободные члены в правую часть, получим
Используя уравнение (3) получим
Ответ: 
2) Решить уравнение 
Видно, что в этом уравнении есть один отрицательный свободный член – 4. Но, перенося его в правую часть уравнения еще с одним отрицательным знаком, получим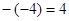 
, тогда
Отсюда
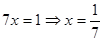
Ответ: 
3) Решить уравнение 
В этом уравнении один коэффициент отрицательный, перенося его и еще с положительным знаком в левую часть нет смысла, т.к. 
, тогда
Отсюда
Ответ: 
4) 
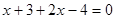
Используя объяснения к уравнению 2), получим
Отсюда
Ответ: 
5) 
Используя объяснения, приведенные к уравнениям 1), 2), 3), 4), получим
Отсюда
Ответ: 
2. Пусть дано линейное уравнение вида
(4)
В отличие от уравнения (1) переменные, содержащие коэффициенты, переносятся в левую часть с отрицательным знаком, в правую часть свободные члены переносятся тоже со знаком отрицательным. Но свободный член 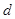в уравнении (4) и так стоит в правой части, поэтому он не будет менять знак, поменяет знак только член . И так, решим уравнение (4).
Перенесем переменные с коэффициентами в левую часть с отрицательным знаком, а член в правую часть тоже с отрицательным знаком, получим
(5)
Отсюда
Если 
, то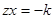 
Решение уравнения (4) можно записать в виде системы
(6)
Пример. Решить уравнение 
Перенесем неизвестные с коэффициентами в левую часть с отрицательным знаком, а член 
в правую часть со знаком «минус», тогда
Отсюда
Ответ: 
3. Линейное уравнение с двумя переменными имеет вид:
(7)
Для решения уравнения (7) выразим переменную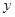 
через переменную 
, т.е. получим уравнение вида
(8)
Для нахождения решения уравнения (7) в уравнении (8) выбирается произвольное (любое) значение . Таким образом, уравнение (7) обладает множеством решений.
Пример. Решить уравнение 
Воспользуемся формулой (8), тогда
Теперь выберем абсолютно любое значение икса, например, при
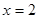, получим
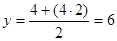
Ответ: 
Квадратные уравнения.
Уравнение второй степени вида 
называется квадратным. Для решения такого уравнения воспользуемся следующими формулами:
и 
(9)
Где 
и 
- корни квадратного уравнения
Пусть 
, тогда если 
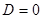, то можно записать
(10)
Если 
, то уравнение не имеет решений.
Пример. Решить уравнение 
Пользуясь формулами (9) получим
Ответ: 
и 
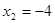
Уравнение третей степени.
Уравнение третей степени вида 
называется кубичным уравнением. Для решения такого уравнения заменим неизвестное - 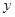на коэффициент 
и вводя подстановку 
Получим более упрощенное уравнение третей степени
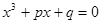(11)
Поскольку уравнение в третей степени, то соответственно решениями этого уравнения будут три корня, которые сейчас определим из следующей системы
(12)
Корни 
- есть решения уравнения, где 
- комплексное число.