Дифракция
В данном уроке речь пойдёт о дифракции света, еще одном явлении, которое присущее только волновым процессам.
В прошлой теме рассмотрели явление интерференции света, т.е. явления наложения световых когерентных волн, в результате которого наблюдается устойчивая во времени картина чередования максимумов и минимумов интенсивности света.
Были выведены условия интерференционных максимумов и минимумов. Было установлено, что явление интерференции присуще только волновым процессам.
Но, если свет — это волна, то помимо явления интерференции света, должно также наблюдаться и явление дифракции — огибание волнами препятствий. Тени от мелких предметов выглядят достаточно резко. Как же тогда пронаблюдать явление дифракции, если оно действительно существует? Для этого рассмотрим опыт. Перед источником света поставим преграду — круглый металлический шарик, а вместо щели возьмем треугольное отверстие. Теперь в центре тени появилось светлое пятно треугольной формы. Значит, за непрозрачной преградой видно изображение источника света. Свет, как бы проникает внутрь тени, огибая при этом препятствие.
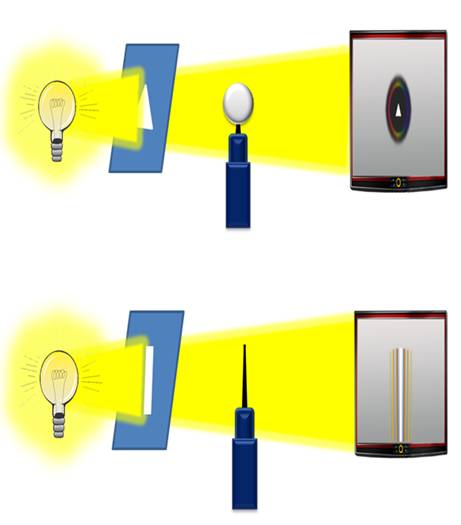
Это явление и называют дифракцией света.
И так, дифракцией света называется совокупность оптических явлений, обусловленных волновой природой света и наблюдающихся при его распространении в среде с резко выраженными неоднородностями. В результате происходит огибание волнами препятствий, размеры которых соизмеримы с длиной волны.
Впервые на эту особенность обратил внимание Леонардо Да Винчи. Гримальди подробно описал ее в 1665 году. Но лишь в начале 19 века нашел этому явлению объяснение французский физик Огюст Френель. Френель писал работу на конкурс, организованный Академией наук Франции, где им были изучены явления интерференции и дифракции света.
В начале, в своих работах, Френель пытался объяснить явление дифракции с помощью принципа Гюйгенса, согласно которому, как мы уже знаем, каждая точка, до которой доходит волна, является центром вторичных сферических когерентных волн, а огибающая этих волн дает положение нового фронта волны в следующий момент времени. Однако, как оказалось, с помощью данного принципа можно решить задачу о направлении распространения волнового фронта, но нельзя выяснить, от чего же зависит амплитуда, а, как следствие, и интенсивность волн, распространяющихся по разным направлениям. Поэтому Френелю пришлось развить этот принцип дальше, дополнив его идеей об интерференции вторичных волн. Таким образом, принцип Гюйгенса трансформировался в принцип Гюйгенса-Френеля, согласно которому, каждая точка фронта волны является источником вторичных сферических когерентных волн. При этом новый фронт волны образуется как раз за счет интерференции вторичных волн.
Учет амплитуд и фаз вторичных волн позволяет в каждом конкретном случае найти амплитуду, а, следовательно, и интенсивность результирующей волны в любой точке пространства.
Рассмотрим опыты по дифракции света на круглом отверстии. В качестве источника монохроматического света возьмем лазер. При изменении расстояния диафрагмы от экрана в области тени происходит перераспределение света.
Как это объяснить? По волновой теории Гюйгенса, каждая точка волнового фронта становится источником вторичных волн. Интерферируя, эти вторичные волны и создают наблюдаемую картину на экране. А теперь будем менять размеры диафрагмы.
В центре картины светлое пятно.
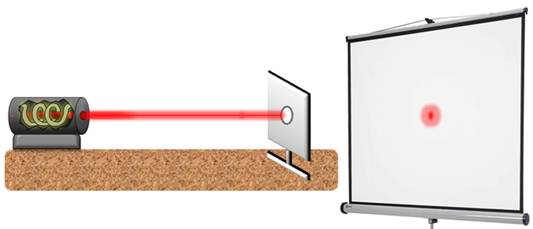
Теперь темное.
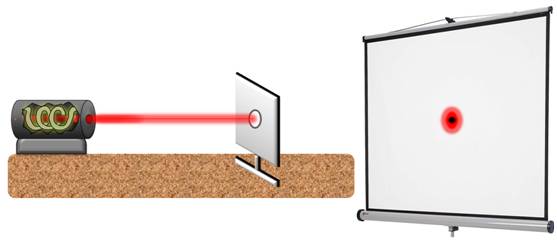
И снова светлое.
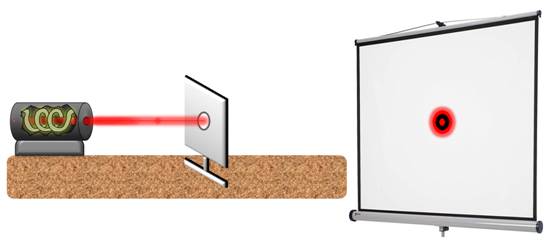
Как можно заметить, изменяется и сама дифракционная картина.
Для объяснения полученной дифракционной картины от круглого отверстия, Френель предложил разбить волновую поверхность на отдельные кольцевые зоны так, чтобы расстояние от соседних зон до точки наблюдения отличались на половину длины волны. Размер диафрагмы ограничивает число действующих зон. В нашем случае, освещенность будет зависть только от действия первой и второй зон. При этом волны от этих зон будут приходить к экрану в противофазе и, следовательно, гасить друг друга. Поэтому в центре дифракционной картины мы наблюдаем темное пятно. Если же мы увеличим отверстие так, чтобы на освещенность экрана влияла еще и третья зона, то в центре появится светлое пятно. Следует учесть, что с увеличением номера зоны будет уменьшаться угол, под которым она видна из точки наблюдения. Вследствие этого уменьшаются и амплитуды волн.
Амплитуда волны в центре дифракционной картины определяется полу суммой волн от первой и последней открытой зоны, когда их число нечетное. И их полу разностью при четном числе зон.
Любопытно отметить, что если оставить открытой только одну первую зону, то амплитуда увеличится в два, а интенсивность в 4 раза, по сравнению с действием всех зон. Таким образом, отверстие, шириной в одну зону Френеля обладает фокусирующим действием.
Еще больший эффект получим, оставив только четные или только нечетные зоны. На этом принципе устроена зонная пластинка Френеля, действующая подобно линзе.
Но самое интересное произошло дальше. Рассматривая расчеты Френеля, член комиссии Пуассон заметил, что они приводят к парадоксальному результату: согласно Френелю за большим круглым непрозрачным телом прямо в середине его геометрической тени должно возникать небольшое светлое пятно. Очевидную абсурдность этого результата Пуассон хотел использовать как главный аргумент против теории дифракции Френеля, однако, Доминик Араго поставил эксперимент, подтвердивший это предсказание. В итоге полученный результат, ставший известным как пятно Араго — Пуассона, оказался весомым аргументом в пользу новой волновой теории.
В наши дни важную роль в прикладной оптике играют явления дифракции на отверстиях в форме щели с параллельными краями. Но использование дифракции света на одной щели затруднено из-за очень слабой видимости дифракционной картины. Выходом из этой трудной ситуации стало создание дифракционной решетки.
Дифракционная решетка — это спектральный прибор, служащий для разложения света в спектр и измерения длины волны. Она представляет собой совокупность большого числа параллельных штрихов одинаковой формы, нанесенных на плоскую или вогнутую полированную поверхность на одинаковом расстоянии друг от друга.
Рассмотрим плоскую прозрачную дифракционную решетку. Обозначим ширину прозрачного штриха через a, а ширину непрозрачного промежутка через b.
Сумму ширины прозрачного участка и ширины непрозрачного промежутка называют постоянной (или периодом) дифракционной решетки. Она также обратно пропорциональна числу штрихов на единицу длины решетки. Обычно дается число штрихов на миллиметр.
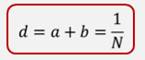
Пусть плоская монохроматическая волна падает нормально к плоскости решетки. Тогда, согласно принципу Гюйгенса-Френеля, каждая щель будет являться источником вторичных волн, способных интерферировать друг с другом. Если за дифракционной решеткой установить линзу, то в ее фокальной плоскости можно будет наблюдать дифракционную картину.
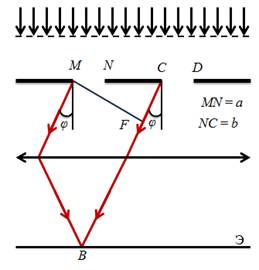
Допустим, что свет дифрагирует на щелях под некоторым углом. Из-за того, что щели находятся на одинаковом расстоянии друг от друга, разности хода лучей, идущих от двух соседних щелей, для данного направления будут одинаковыми в пределах всей дифракционной решетки.
В тех направлениях, для которых разность хода равна четному числу полуволн, будет наблюдаться интерференционный максимум. И, наоборот, для тех направлений, где разность хода равна нечетному числу полуволн, наблюдается интерференционный минимум. Тогда, в направлениях, для которых углы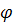 
будут удовлетворять условию
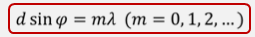
Эту формулу часто называют формулой дифракционной решетки. В ней m — это порядок главного максимума.m=0 обозначают центральный максимум, угол отклонения луча (как видно из формулы) тоже ноль. Если же нас интересует, например, где находится максимум второго порядка для красного света, то, зная длину волны этого красного света и период решетки, мы можем определить синус угла, на который отклонится луч после прохождения дифракционной решетки. Знаем синус – знаем угол. А, зная расстояние от решетки до экрана, по этому углу можем найти расстояние от центрального максимума до максимума второго порядка, который и искали (геометрическая задачка на прямоугольный треугольник).
Если наблюдать дифракцию в белом свете, то можно заметить, что все главные максимумы, кроме центрального нулевого, будут окрашены. Это и понятно, ведь различным длинам волн соответствуют различные углы, на которых наблюдаются интерференционные максимумы.
В настоящее время оптические приборы с дифракционными решетками получили широкое распространение, как в физике, астрономии, так и в химии, биологии, технике. С их помощью изучаются спектры отражения и поглощения веществ, оптические свойства различных материалов. Благодаря дифракции света нам удалось глубже проникнуть в удивительный мир живых клеток, расширить наши познания о далеком прошлом и настоящем нашей вселенной.
Поперечность световых волн. Поляризация света
Явления интерференции и дифракции не оставляют сомнений в том, что распространяющийся свет обладает свойствами волн. Но каких волн — продольных или поперечных?
Длительное время основатели волновой оптики Юнг и Френель считали световые волны продольными, т. е. подобными звуковым волнам. В то время световые волны рассматривались как упругие волны в эфире, заполняющем пространство и проникающем внутрь всех тел. Такие волны, казалось, не могли быть поперечными, так как поперечные волны, в соответствии с воззрениями того времени, могут существовать только в твердом теле. Но как могут тела двигаться в твердом эфире, не встречая сопротивления? Ведь эфир не должен препятствовать движению тел. В противном случае не выполнялся бы закон инерции.
Однако постепенно накапливалось все больше и больше экспериментальных фактов, которые никак не удавалось истолковать, считая световые волны продольными.
Опыты с турмалином. Рассмотрим подробно один из таких экспериментов, очень простой и эффектный. Это опыт с кристаллами турмалина (прозрачными кристаллами зеленой окраски).
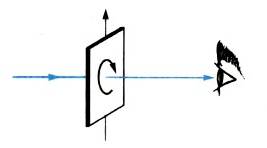
Кристалл турмалина принадлежит к числу так называемых одноосных кристаллов. Возьмем прямоугольную пластину турмалина, вырезанную таким образом, чтобы одна из ее граней была параллельна оси кристалла. Если направить нормально на такую пластину пучок света от электрической лампы или солнца, то вращение пластины вокруг пучка никакого изменения интенсивности света, прошедшего через нее, не вызовет (рис. 1). Можно подумать, что свет только частично поглотился в турмалине и приобрел зеленоватую окраску. Больше ничего, кажется, и не произошло. Но это не так. Световая волна проявила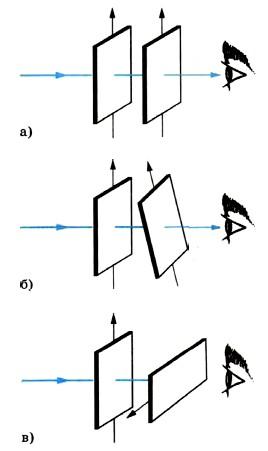 
новые свои свойства.
Эти новые свойства проявляются, если пучок света заставить пройти через второй точно такой же кристалл турмалина (рис. 2, а), параллельный первому. При одинаково направленных осях кристаллов опять ничего интересного не происходит: просто световой пучок еще более ослабляется за счет поглощения во втором кристалле. Но если второй кристалл вращать, оставляя первый неподвижным (рис. 2, б), то обнаружится удивительное явление — гашение света. По мере увеличения угла между осями интенсивность света уменьшается. И когда оси перпендикулярны друг другу, свет не проходит совсем (рис. 2, в). Он целиком поглощается вторым кристаллом. Как это можно объяснить?
Поперечность световых волн. Из описанных выше опытов следуют два вывода: во-первых, световая волна, идущая от источника света, полностью симметрична относительно направления распространения (при вращении кристалла вокруг луча в первом опыте интенсивность не менялась); во-вторых, волна, вышедшая из первого кристалла, не обладает осевой симметрией (в зависимости от поворота второго кристалла относительно луча интенсивность прошедшего света изменяется).
Продольные волны обладают полной симметрией по отношению к направлению распространения (колебания происходят вдоль этого направления, и оно является осью симметрии волны). Поэтому объяснить опыт с вращением второй пластины, считая световую волну продольной, невозможно.
Полное объяснение опыта можно получить, сделав два предположения.
Первое предположение относится к самому свету. Свет — поперечная волна. В падающем от обычного источника пучке световых волн происходят колебания всевозможных направлений, перпендикулярных направлению распространения волн (рис. 3).
Согласно этому предположению световая волна обладает осевой симметрией, являясь в то же время поперечной. Волны, например, на поверхности воды такой симметрией не обладают, так как колебания частиц воды происходят только в вертикальной плоскости.
Световой поток, в котором колебания происходят по всем направлениям, перпендикулярным направлению распространения волн, называется естественным светом. Такое название оправданно, так как в обычных условиях источники света излучают такой поток. Данное предположение объясняет результат первого опыта. Вращение кристалла турмалина не меняет интенсивность прошедшего света, потому что падающая волна обладает осевой симметрией (несмотря на то, что она поперечная).
Второе предположение относится не к световой волне, а к кристаллу. Кристалл турмалина обладает способностью пропускать световые волны с колебаниями, происходящими в одной определенной плоскости (плоскость Р на рисунке 4). Такой свет называется поляризованным или, точнее, плоскополяризованным в отличие от естественного света, который может быть назван также неполяризованным.
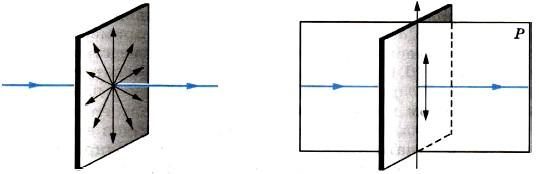
Рисунок 3 Рисунок 4
Это предположение полностью объясняет результаты второго опыта. Из первого кристалла выходит плоскополяризованная волна. При скрещенных кристаллах (угол между их осями 90°) она не проходит сквозь второй кристалл. Если оси кристаллов составляют между собой некоторый угол, отличный от 90°, то проходят колебания, амплитуда которых равна проекции амплитуды волны, прошедшей через первый кристалл, на направление оси второго кристалла.
Итак, кристалл турмалина преобразует естественный свет в плоскополяризованный.
Механическая модель опытов с турмалином. Нетрудно построить простую наглядную механическую модель рассматриваемого явления. Можно получить поперечную волну в резиновом шнуре так, чтобы колебания быстро меняли свое направление в пространстве. Это аналог естественной световой волны. Пропустим теперь шнур сквозь узкий деревянный ящик (рис. 5). Из колебаний всевозможных направлений ящик «выделяет» колебания в одной определенной плоскости. Поэтому из ящика выходит поляризованная волна. Если на ее пути имеется еще точно такой же ящик, но повернутый относительно первого на 90°, то колебания сквозь него не проходят. Волна целиком гасится.
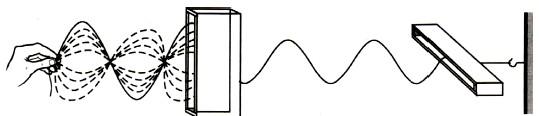
Рисунок 5
Поляроиды. Не только кристаллы турмалина способны поляризовать свет. Таким же свойством, например, обладают так называемые поляроиды. Поляроид представляет собой тонкую (0,1 мм) пленку кристаллов герапатита, нанесенную на целлулоид или стеклянную пластинку. С поляроидом можно провести те же опыты, что и с кристаллом турмалина. Преимущество поляроидов в том, что можно получать большие поверхности, поляризующие свет. К недостаткам поляроидов относится фиолетовый оттенок, который они придают белому свету.
Вывод: Прямыми опытами доказано, что световая волна является поперечной. В поляризованной световой волне колебания происходят в строго определенном — поперечном направлении.